Properties of Logarithmic & Logistic Functions & Graphs (DP IB Applications & Interpretation (AI)): Revision Note
Did this video help you?
Logarithmic functions & graphs
What are the key features of logarithmic graphs?
A logarithmic function is of the form
Remember the natural logarithmic function
This is the inverse of
and
The graphs will always pass through the point (1, a)
The graphs do not have a y-intercept
The graphs have a vertical asymptote at the y-axis:
The graphs have one root at
This can be found using your GDC
The graphs do not have any minimum or maximum points
The value of b determines whether the graph is increasing or decreasing
If b is positive then the graph is increasing
If b is negative then the graph is decreasing
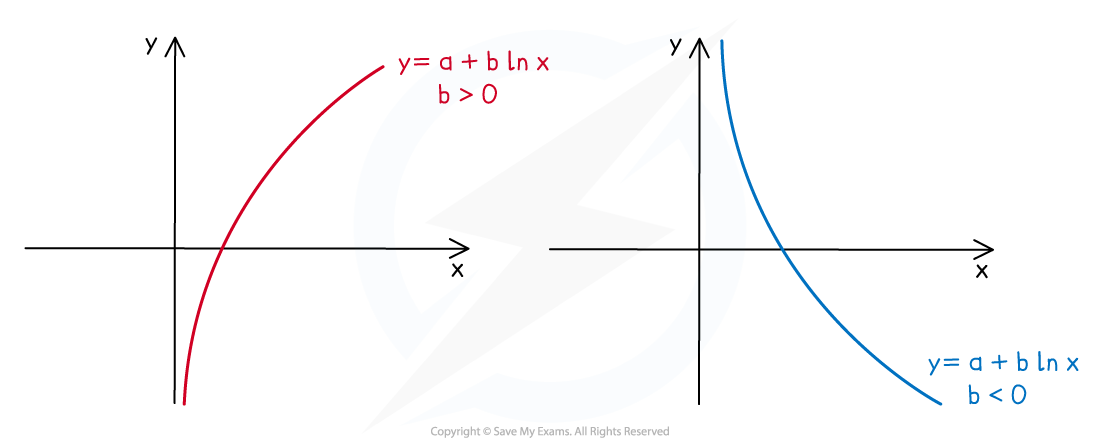
Logistic functions & graphs
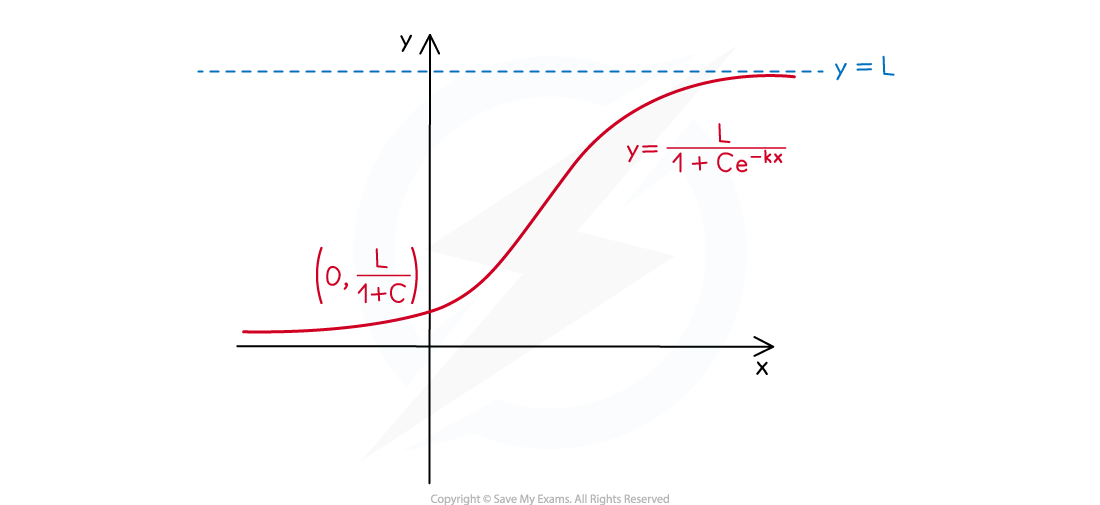
What are the key features of logistic graphs?
A logistic function is of the form
L, C & k are positive constants
Its domain is the set of all real values
Its range is the set of real positive values less than L
The y-intercept is at the point
There are no roots
There is a horizontal asymptote at y = L
This is called the carrying capacity
This is the upper limit of the function
For example: it could represent the limit of a population size
There is a horizontal asymptote at y = 0
The graph is always increasing
Ready to test your students on this topic?
- Create exam-aligned tests in minutes
- Differentiate easily with tiered difficulty
- Trusted for all assessment types

Did this page help you?