Linear Trigonometric Equations (DP IB Analysis & Approaches (AA)): Revision Note
Did this video help you?
Trigonometric equations: sinx = k
How do I solve trigonometric equations?
Rearrange the equation to isolate the trig term
e.g. rearrange
to
You can then find all the solutions using the trig graphs or the unit circle
The steps are summarised below
sinx = k & cosx = k
STEP 1
Find the principal value using the inverse trig functionsYou might have to use your GDC or your knowledge of exact trig values
e.g. for
you find
e.g. for
you find
STEP 2
Find a second angleFor
: subtract the principal angle from 180°
e.g.
For
: subtract the principal angle from 360°
e.g.
STEP 3
Find all the angles in the given interval by adding or subtracting multiples of 360° to your two anglese.g.
and
e.g.
and
Examiner Tips and Tricks
For , you can also find a second angle by simply changing the sign of the principal value. For example, if
is a solution to
, then so is
.
tanx = k
STEP 1
Find the principal value using the inverse trig functionsYou might have to use your GDC or your knowledge of exact trig values
e.g. for
you find
STEP 2
Find all the angles in the given interval by adding or subtracting multiples of 180° to your principal anglee.g.
and
Examiner Tips and Tricks
The equation could use degrees or radians. Make sure you change the angle mode of your GDC to match the question. And remember the two key conversions:
180° = π radians
360° = 2π radians
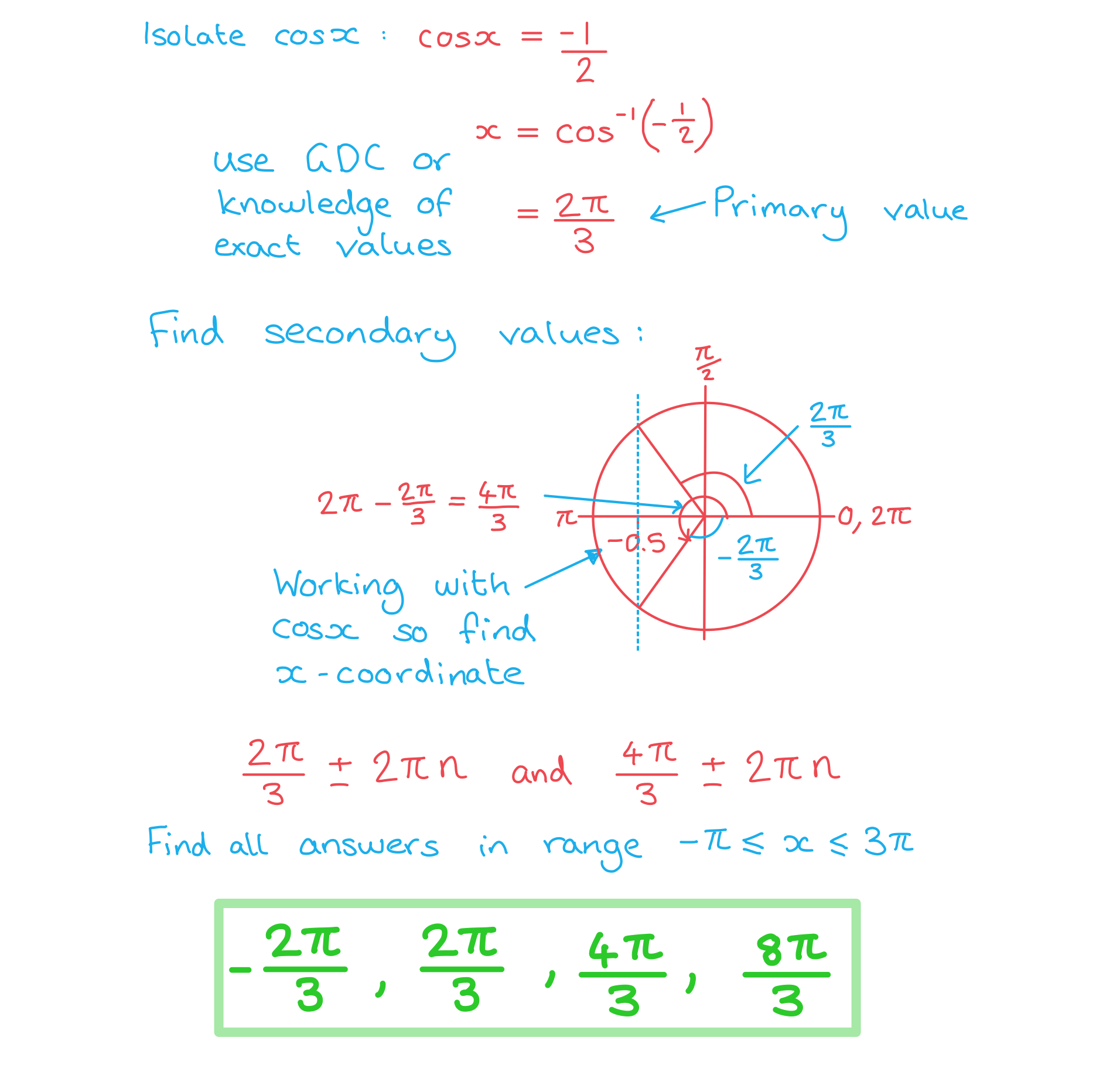
Worked Example
Solve the equation , finding all solutions in the range
.
Did this video help you?
Trigonometric equations: sin(ax + b) = k
How can I solve equations with transformations of trig functions?
STEP 1
Make the substitutione.g. for
:
let
the equation becomes
STEP 2
Write the interval in terms of the substitutione.g. for the interval
:
multiply each part by 2 and add 60°
the interval becomes
this is the same as
STEP 3
Find all the solutions forthat are in the interval
e.g.
⨉ is outside the interval
STEP 4
Find the value offor each value of
using the substitution
Examiner Tips and Tricks
A common error that students make is dealing with the interval incorrectly. If the substation is , then you multiply the interval by 2 and then add 60°. However, a mistake is when students do the opposite: subtract 60° and then divide by 2.
Worked Example
Solve the equation , finding all solutions in the range
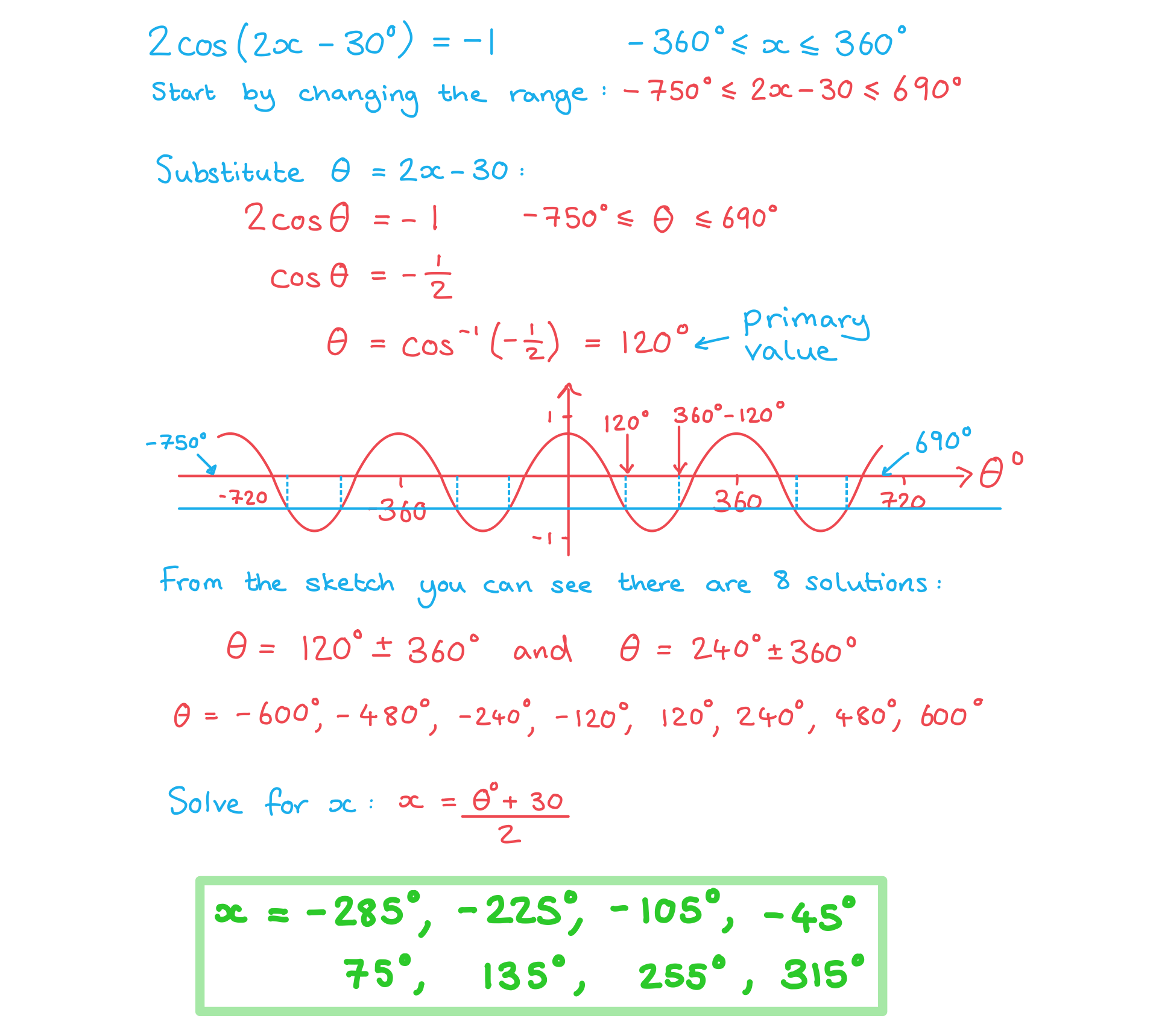

Unlock more, it's free!
Did this page help you?