Revision NotesExam QuestionsPast Papers
GCSEFurther MathsAQARevision Notes3. Coordinate GeometryEquation of a CircleEquation of a Circle

Equation of a Circle (AQA GCSE Further Maths) : Revision Note

Paul

Written by: Paul

Reviewed by: Dan Finlay

Updated on

Equation of a Circle

What do I need to know about the equation of a circle?

  • A circle with centre (a, b) and radius r has the equation

 

Eqn of Circle graph illustr, A Level & AS Level Pure Maths Revision Notes

  •  You need to be able to find the centre and radius of a circle from its equation 

Eqn of Circle Illustr 1, A Level & AS Level Pure Maths Revision Notes

  •  You need to be able to find the equation of a circle given its centre and radius 

Eqn of Circle Illustr 2, A Level & AS Level Pure Maths Revision Notes

Examiner Tips and Tricks

  • Remember that the numbers in the brackets have the opposite signs to the coordinates of the centre. 

    Eqn of Circle sign flip, A Level & AS Level Pure Maths Revision Notes

     

  • Don't forget to take the square root of the right-hand side of the equation when finding the radius.

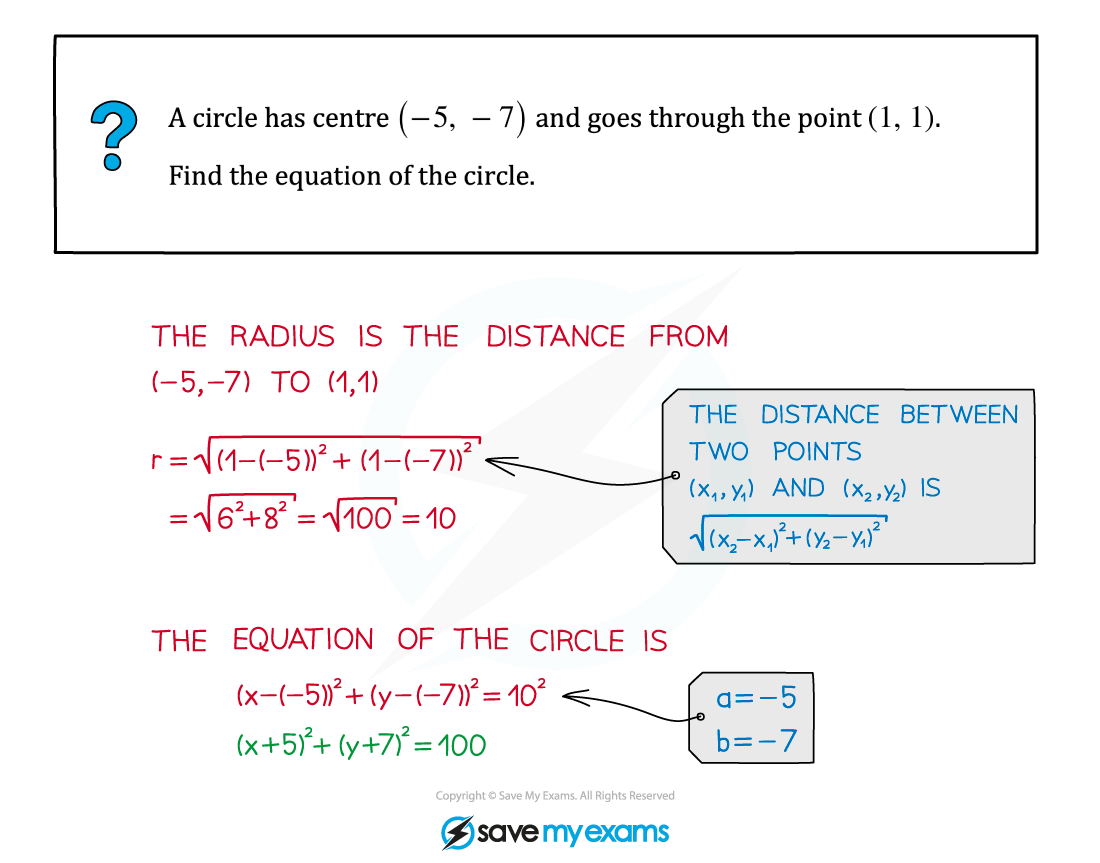
Worked Example

Eqn of Circle Example, A Level & AS Level Pure Maths Revision Notes

Intersection of a Circle and a Line

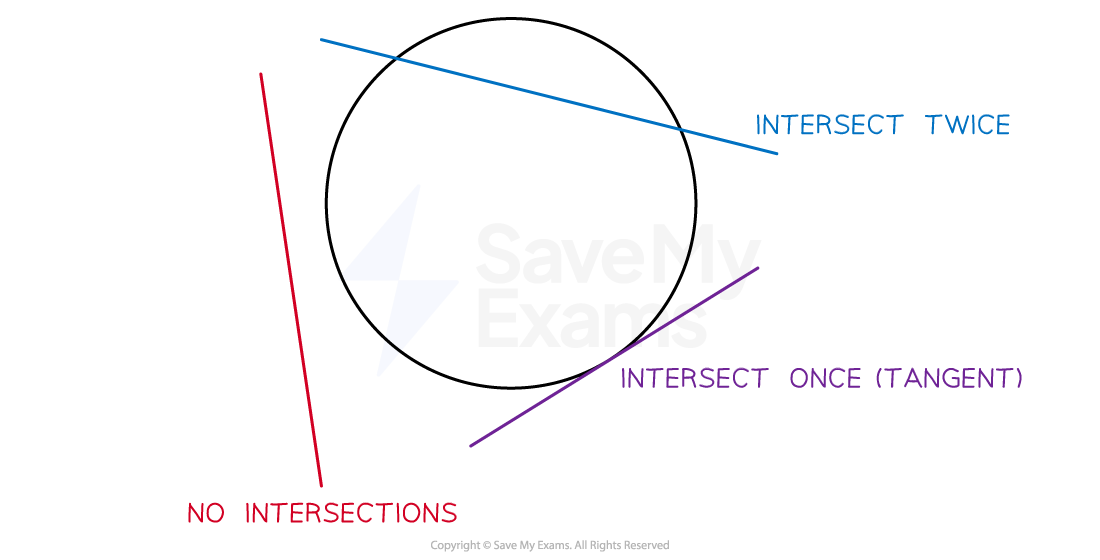
How can a circle and a straight line intersect?

  • A circle and a straight line could

    • intersect at two distinct (different) points

    • intersect at one point only

      • in this case the line would be tangent to the circle

    • not intersect at all

equation-of-a-circle-rn-image

How do I find the intersections between a line and a circle?

  • As with two straight lines, this is a matter of solving the two equations simultaneously

    • However the equation for the circle is quadratic so the method involves more steps

  • First, ensure that the equation for the circle is in the form open parentheses x minus a close parentheses squared plus open parentheses y minus b close parentheses squared equals r squared

    • Where the centre of the circle is (a, b) and its radius is r

  • Also ensure the equation for the straight line is in the form y equals m x plus c 

    • m is the gradient and c is the y-axis intercept

  • One or both equations may need deducing from a sketch or information given in a question

    • They may need to be rearranged to get them in the correct format

STEP 1
Substitute the equation of the straight line into the equation of the circle for y
e.g.

For the circle open parentheses x minus 2 close parentheses squared plus open parentheses y minus 3 close parentheses squared equals 2 squared and straight line y equals x minus 1

substituting the line into the circle would give

open parentheses x minus 2 close parentheses squared plus open parentheses open parentheses bold italic x bold minus bold 1 close parentheses minus 3 close parentheses squared equals 2 squared

STEP 2

Expand and simplify to give a quadratic equation in x

Quadratic equations are easiest to deal with once in the form "a x squared plus b x plus c equals 0"

e.g.

table row cell open parentheses x minus 2 close parentheses squared plus open parentheses x minus 4 close parentheses squared end cell equals 4 row cell x squared minus 4 x plus 4 plus x squared minus 8 x plus 16 minus 4 end cell equals 0 row cell 2 x squared minus 12 x plus 16 end cell equals 0 row cell x squared minus 6 x plus 8 end cell equals 0 end table

STEP 3
Solve the quadratic equation to find the x-coordinates of the points of intersection

e.g.

table row cell open parentheses x minus 2 close parentheses open parentheses x minus 4 close parentheses end cell equals 0 row x equals 2 row x equals 4 end table

STEP 4
Substitute the x-coordinates into the equation of the straight line to find the y-coordinates

(You could use the circle equation here but that's normally harder!)

e.g.

table attributes columnalign right center left columnspacing 0px end attributes row y equals cell 2 minus 1 equals 1 end cell row y equals cell 4 minus 1 equals 3 end cell end table

STEP 5

Write your final answer as coordinate pairs

e.g.

open parentheses 2 comma space 1 close parentheses and open parentheses 4 comma space 3 close parentheses

  • The number of solutions to the quadratic equation will determine the number of intersections between the line and the equation (or vice versa)

    • a quadratic with two (real) solutions will indicate two intersections

    • a quadratic with only one (real) solution (or a repeated (real) solution) will indicate one intersection

      • so the line would be a tangent to the circle

    • a quadratic with no (real) solutions will indicate the line and circle do not intersect

Worked Example

An equation with centre (-3, 2) and radius 4 intersects the straight line with equation y equals x plus 1 at two points, A and B.
Find the coordinates of points A and B.
 
Write the equation of the circle using the information given, the centre is (-3, 2) and the radius is 4

open parentheses x plus 3 close parentheses squared plus open parentheses y minus 2 close parentheses squared equals 4 squared open parentheses x plus 3 close parentheses squared plus open parentheses y minus 2 close parentheses squared equals 16

Substitute the equation of the line, y equals x plus 1, for y, and simplify

table attributes columnalign right center left columnspacing 0px end attributes row cell open parentheses x plus 3 close parentheses squared plus open parentheses open parentheses bold italic x bold plus bold 1 close parentheses minus 2 close parentheses squared end cell equals 16 row cell open parentheses x plus 3 close parentheses squared plus open parentheses x minus 1 close parentheses squared end cell equals 16 end table

Expand the brackets, simplify, and equate to zero

table row cell x squared plus 6 x plus 9 plus x squared minus 2 x plus 1 end cell equals 16 row cell 2 x squared plus 4 x plus 10 end cell equals 16 row cell 2 x squared plus 4 x minus 6 end cell equals 0 end table

We now need to solve the quadratic
As all the coefficients are even, we can divide both sides by 2 to make this easier

x squared plus 2 x minus 3 equals 0

Factorise and solve for x

open parentheses x plus 3 close parentheses open parentheses x minus 1 close parentheses equals 0 x equals negative 3 space comma space space x equals 1

These are the x-coordinates of the points of intersection of the line and the circle
To find the y-coordinates, substitute these into the equation of the line; y equals x plus 1

x equals negative 3 space colon space space space y equals open parentheses negative 3 close parentheses plus 1 equals negative 2 x equals 1 space colon space space space space space space space y equals open parentheses 1 close parentheses plus 1 equals 2

Write the coordinate pairs as your final answer
Be careful to match the corresponding x and y values correctly

stretchy left parenthesis negative 3 comma space minus 2 stretchy right parenthesis stretchy left parenthesis 1 comma space 2 stretchy right parenthesis

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Equation of a Straight LineNext:Tangents to Circles
    Author
    Reviewer
    Paul

    Author: Paul

    Expertise: Maths Content Creator (Previous)

    Paul has taught mathematics for 20 years and has been an examiner for Edexcel for over a decade. GCSE, A level, pure, mechanics, statistics, discrete – if it’s in a Maths exam, Paul will know about it. Paul is a passionate fan of clear and colourful notes with fascinating diagrams.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.