Geometric Proof (AQA GCSE Further Maths) : Revision Note
Geometric Proof
What is a geometric proof?
Geometric proof involves using known rules about geometry to prove a new statement about geometry
A proof question might start with “Prove…” or “Show that …”
The rules that you might need to use to complete a proof include;
Basic angle facts and properties of 2D shapes
Examples
"the angles sum in any quadrilateral is 360°"
"an isosceles triangle has two equal sides/two equal angles"
"vertically opposite angles are equal"
Angles involved with parallel lines
alternate and corresponding angles
Circle theorems
there are a few of these!
these are dealt with separately in the revision note Algebraic Circle Theorems
Pythagoras' theorem (only applies to right-angled triangles)
where
is the hypotenuse
Congruence and similarity
congruent shapes are identical
similar shapes have equal angles; side lengths are in the same ratio to each other
You will need to be familiar with the vocabulary of the topics above
reasons are often required in order to fully explain a geometrical proof
How do I write a geometric proof?
Usually you will need to write down a few steps to prove the statement
At any step where an angle fact is used you should write down the fact and a reason
do this even for the most basic facts
e.g. angles on a straight line add up to 180°
The proof is complete when you have written down all the steps clearly
Before getting into your steps of working for your proof
underlining key words or facts in the question
mark any important information given in words to a given diagram
add any information (such as line lengths and/or angles) to the diagram using facts you know
you can write down the steps and reasons for these later
What notation should I use?
Labelling vertices (corners) and lengths are done in capital letters
Examples
"from A to B ..."
"side lengths AB and BC are equal..."
"triangle ABC is ..."
Labelling angles can be done by writing "angle ABC"
you may see other ways including
single letters ("angle B")
"hat notation"
"∠ABC" which would be read as "angle ABC"
Of course if an angle is marked with a letter (x or θ are common) use that
If not, you can add your own letters in, but do make them clear on the diagram
Examiner Tips and Tricks
DO show all the key steps - if in doubt, include it
DON'T write in full sentences!
For each step, just write down the fact, followed by the key mathematical reason that justifies it
READ the language of the question carefully
If the question says 'Prove...' then you definitely need to explain your reasoning at each step to get full marks
If the question only says 'Work out...' then the marks will be for correct arithmetic workings using relevant geometric facts
Worked Example
In the diagram below, AC and DG are parallel lines.
B lies on AC.
E and F lie on DG.
BE = BF.
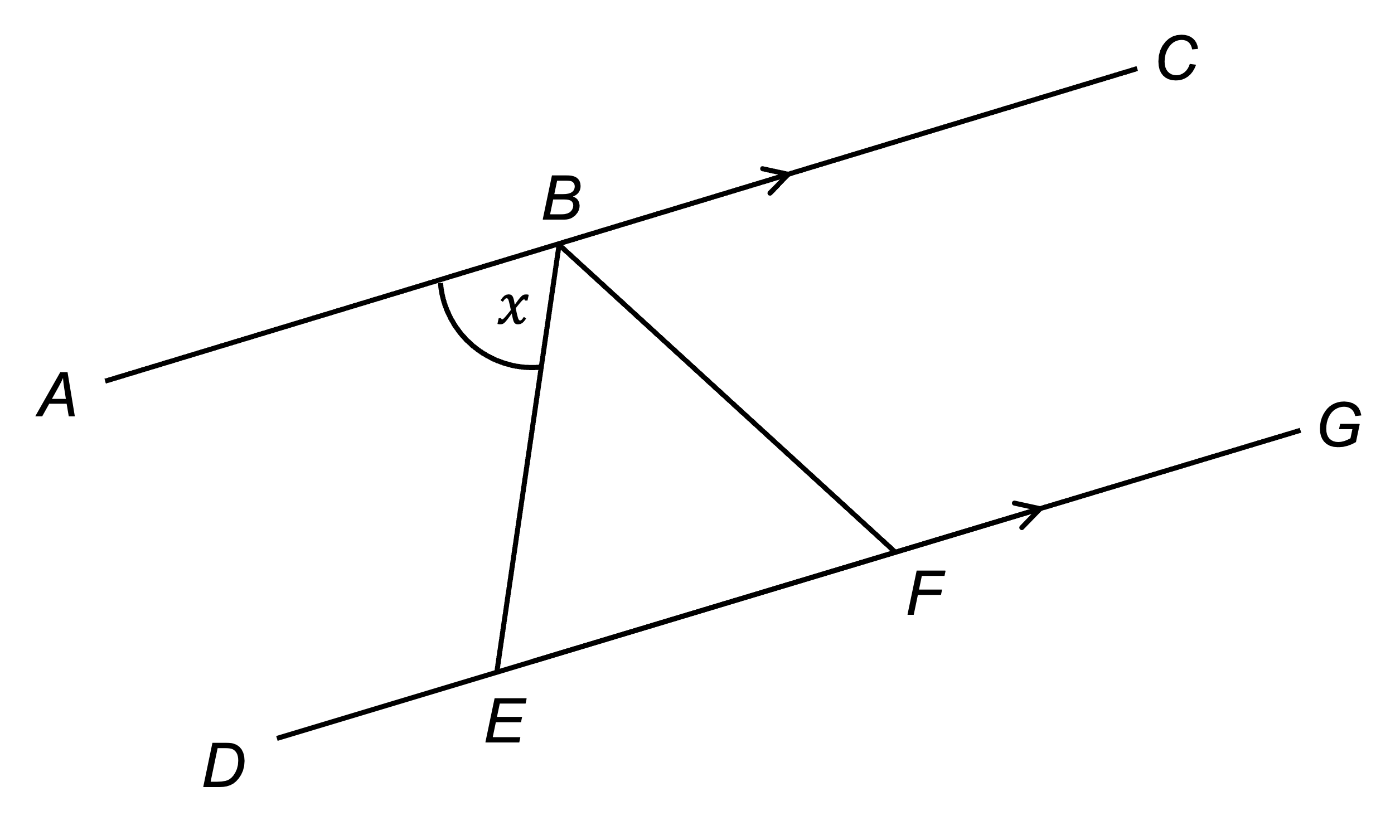
Prove that angle EBF is .
Give reasons for each stage of your working.
Mark BE = BF on the diagram and realise that triangle BEF is isosceles - this may be useful later
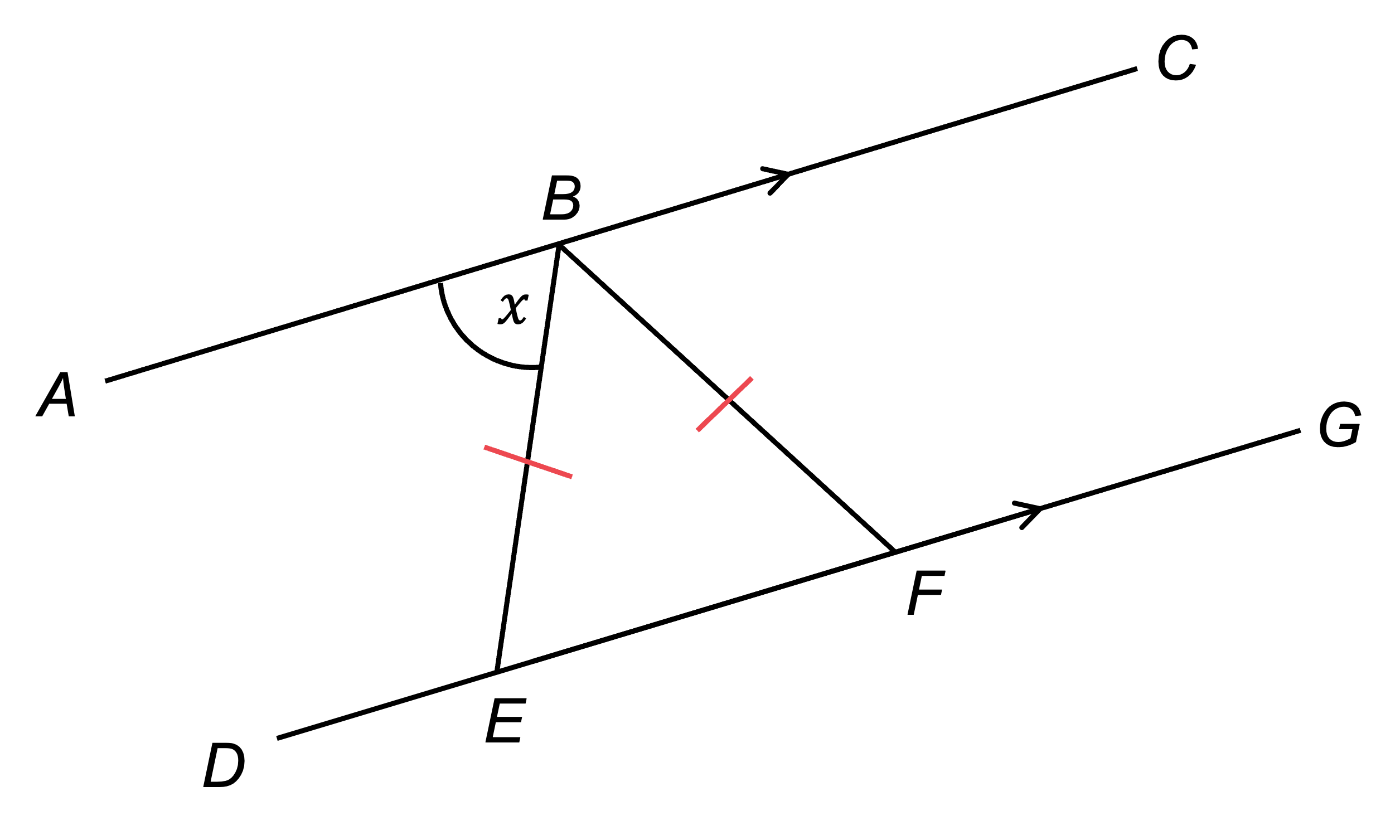
AC and DG are parallel, so using alternate angles
Mark this on the diagram
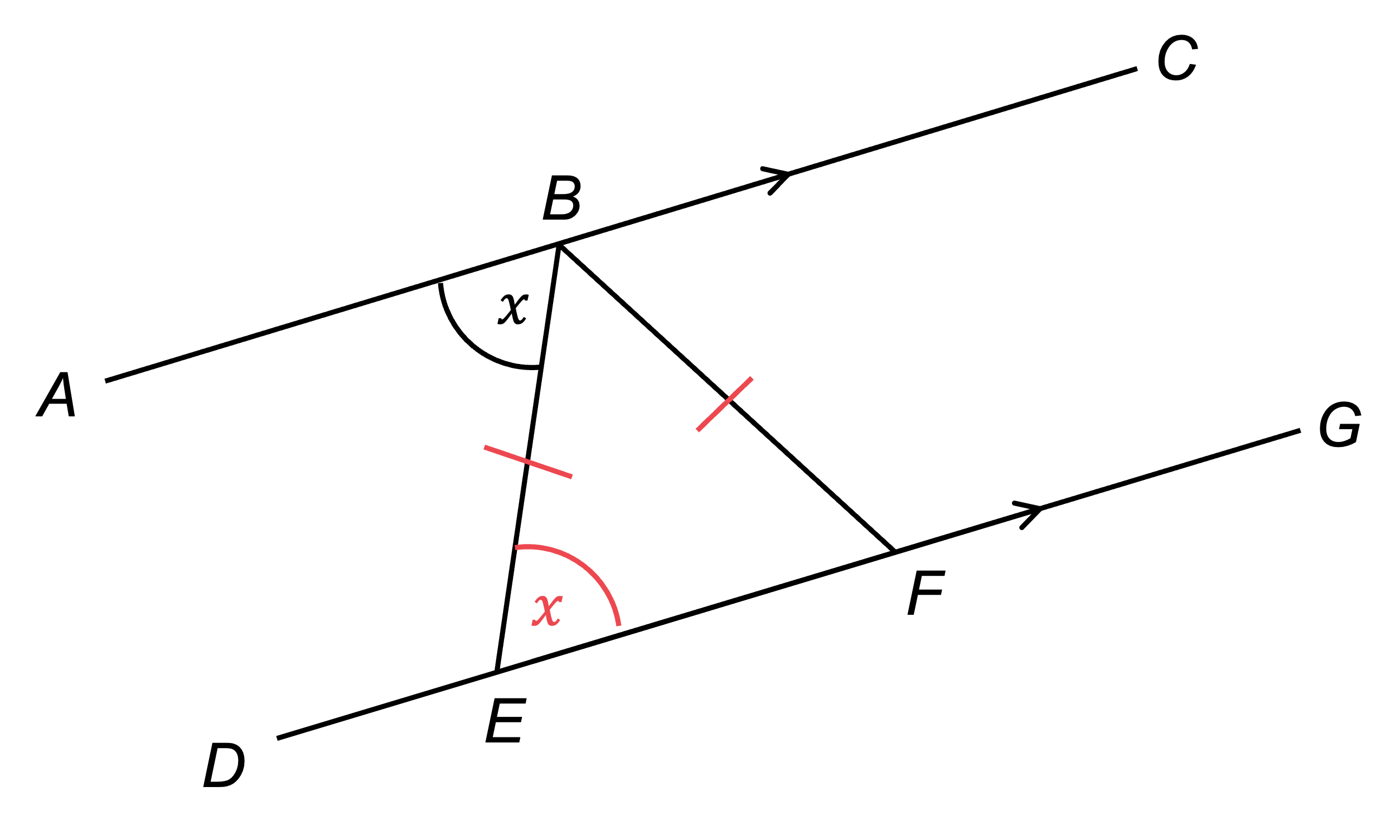
Write the fact, and the reason using mathematical vocabulary
angle BEF = , alternate angles
Using the fact that triangle BEF is isosceles, we can see that angle BFE =
Mark this on the diagram, and write the fact and reason
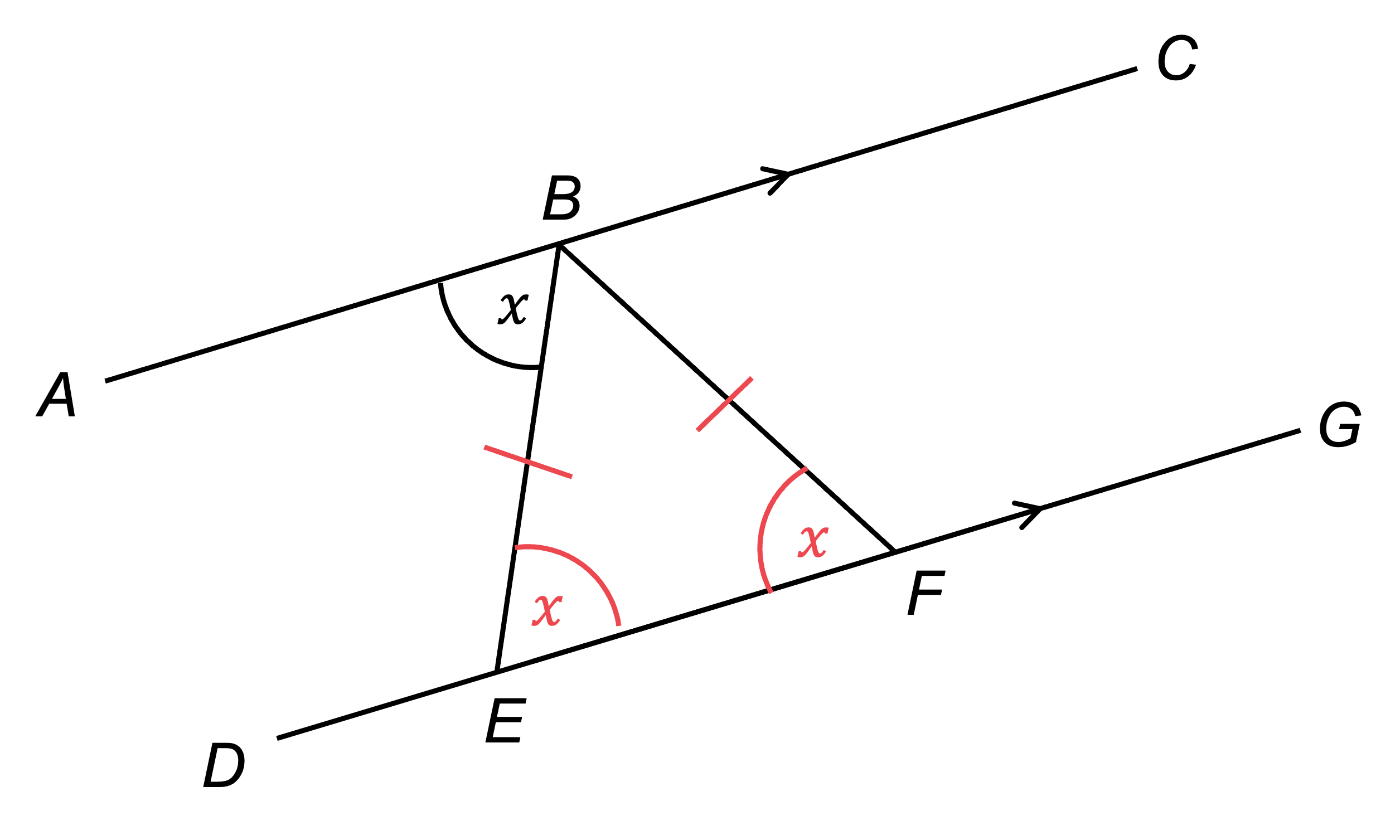
angle BFE = , isosceles triangle
is the last remaining angle in a triangle; the angle sum of a triangle is 180°, so
Write the fact and reason as the last step of your proof
, triangle angle sum is 180°
Algebraic Circle Theorems
What are algebraic circle theorems?
This part of geometric proof focuses on using circle theorems
Here's a reminder of them
the top-right diagram is also called the "Alternate Segment Theorem"
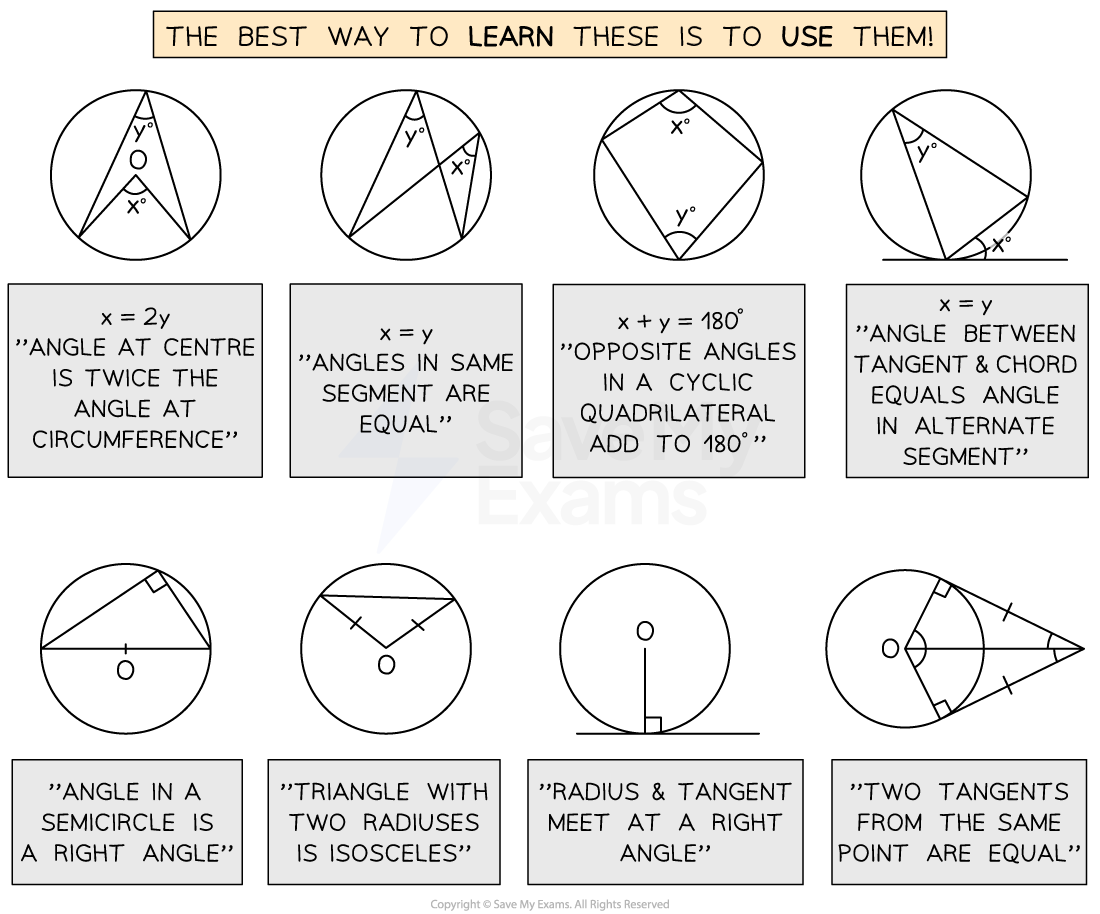
Rather than finding the values of missing angles you may have to
prove/show a result that links two or more unknowns (letters)
e.g. show that "
"
there is no requirement to find the actual values of
and
separately
just that they sum to 90
How do I prove or show a result using circle theorems?
Other skills beyond circle theorems may be involved
angles in basic shapes, parallel lines, congruence, Pythagoras' Theorem, etc
Have in the back of your mind the result you are aiming for
This will help stop you from trying to find values for particular unknowns
which may be impossible
Use angle facts alongside circle theorems to find a relationship between the the unknowns
e.g. if the three angles in a triangle are 65°,
and
, then the fact is
and the reason is that angles in a triangle sum to 180°
You may have to use some basic algebra skills to get the required result
simplifying, factorising, expanding, ...
e.g. if the two non-right angle angles in a triangle in a semi circle are
and
then
but we can then simplify by dividing through by 5 to give
You may be given extra information in later parts of a question that do allow the unknowns to be found
e.g. Having shown
, if we are then told that
then we can find both
and
using simultaneous equations
Examiner Tips and Tricks
You may find it helpful to jot the required result down at the side of your page/working area or next to a diagram
This can act as a reminder to not try to find particular values
Remember to write a "fact" and "reason" for each step of your proof
Read the language of the question carefully
If the question says 'Prove...' then you definitely need to explain your reasoning at each step to get full marks
If the question only says 'Work out...' then the marks will be for correct arithmetic workings using relevant geometric facts
Where allowed, your calculator may have the ability to solve simultaneous equations
Whilst you should write working down, you can use your calculator to check or give you answer(s) to aim for
Worked Example
The diagram below shows a circle with centre O.
ABCD is a cyclic quadrilateral. The line PDQ is tangent to the circle at D.
Angle ABC is , angle CDQ is
and angle ACD is
.
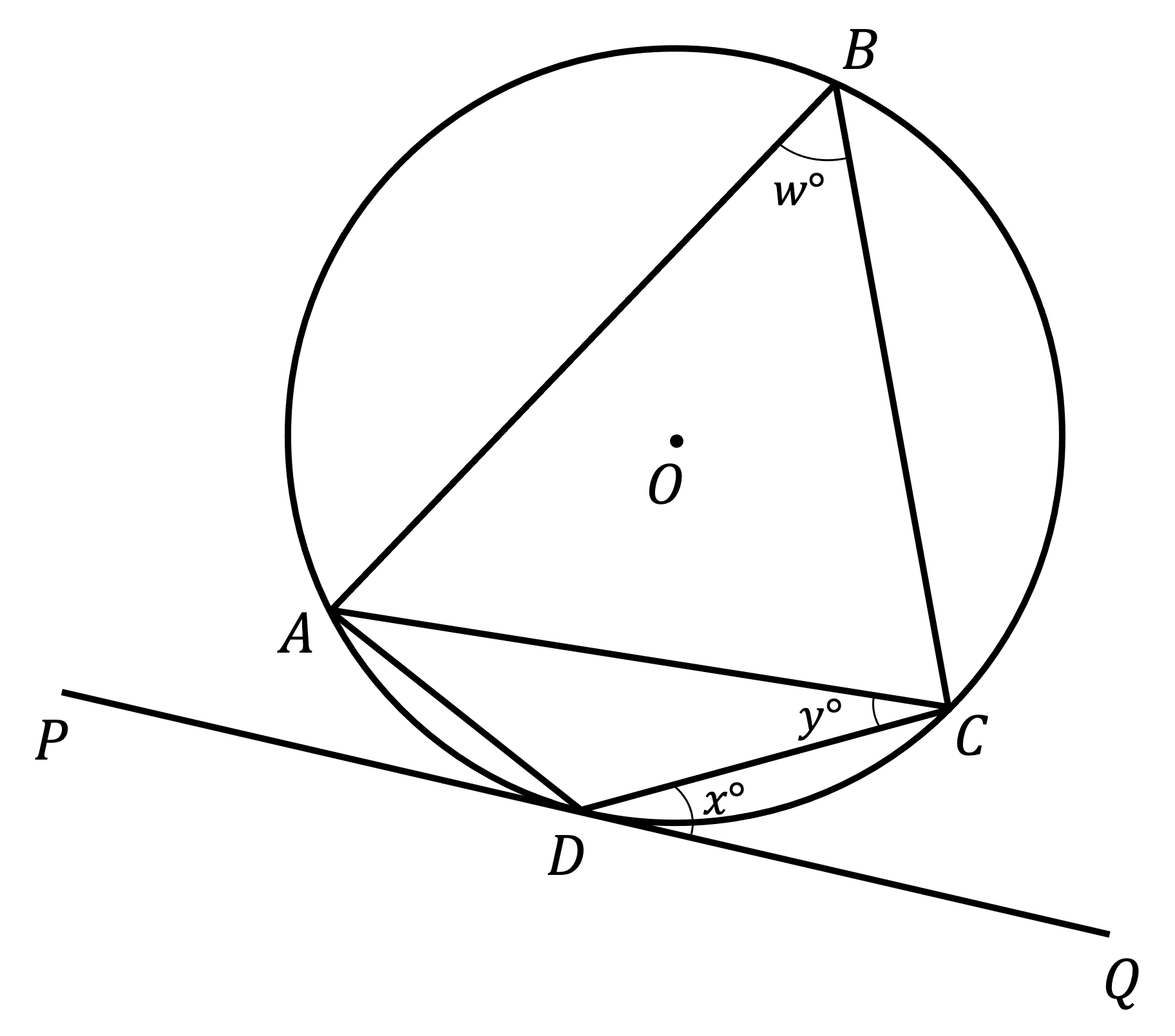
Prove that , giving reasons for each stage of your answer.
BADC is a cyclic quadrilateral
Use this to find angle ADC
angle ADC = 180° - w
opposite angles in a cyclic quadrilateral sum to 180°
Find angle DAC using the Alternate Segment Theorem
angle DAC = x
Alternate Segment Theorem
Use the sum of angles in triangle ADC to form an equation
180° - w + x + y = 180°
angles in a triangle sum to 180°
Rearrange the equation
x + y = w
Present the geometric proof (as "facts" with "reasons")
angle ADC = 180° - w
opposite angles in a cyclic quadrilateral sum to 180°
angle DAC = x
Alternate Segment Theorem
x + y = w
angles in a triangle sum to 180°

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?

