Finding Vector Paths (Edexcel GCSE Maths)

Finding Vector Paths

How do I find the vector between two points?

• A vector path is a path of vectors taking you from a start point to an end point

• The following grid is made up entirely of parallelograms

  • The vectors a and b defined as marked in the diagram:

    • Any vector that goes horizontally to the right along a side of a parallelogram will be equal to a

    • Any vector that goes up diagonally to the right along a side of a parallelogram will be equal to b

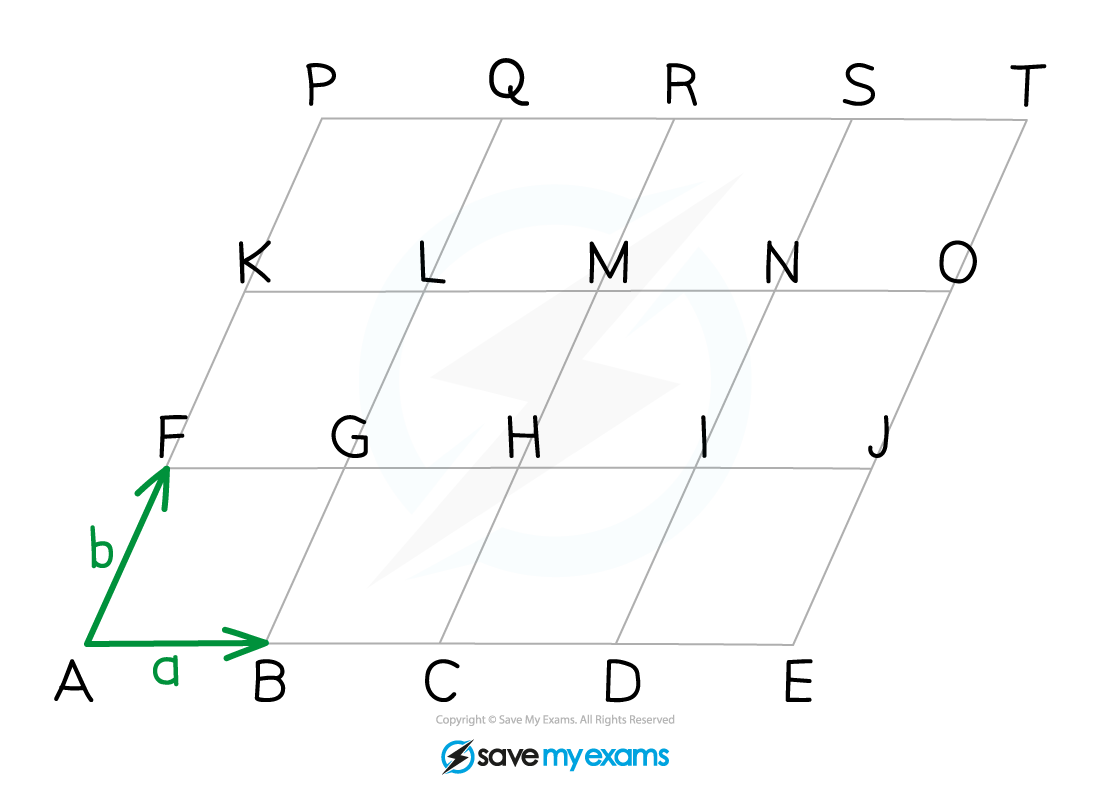
• To find the vector between two points

  • Count how many times you need to go horizontally to the right

    • This will tell you how many a's are in your answer

  • Count how many times you need to go up diagonally to the right

    • This will tell you how many b's are in your answer

  • Add the a's and b's together

    • E.g. 

• You will have to put a negative in front of the vector if it goes in the opposite direction

  • -a is one length horizontally to the left

  • -b is one length down diagonally to the left

    • E.g.  or

    • Likewise,

• It is possible to describe any vector that goes from one point to another in the above diagram in terms of a and b