Revision Notes Exam Questions Past Papers Mock Exams

A LevelMathsCambridge (CIE)Pure 3Revision NotesLogarithms & ExponentialsLaws of LogarithmsLaws of Logarithms

Laws of Logarithms (Cambridge (CIE) A Level Maths) : Revision Note

Last updated

17 January 2025

Did this video help you?

Laws of Logarithms

What are the laws of logarithms?

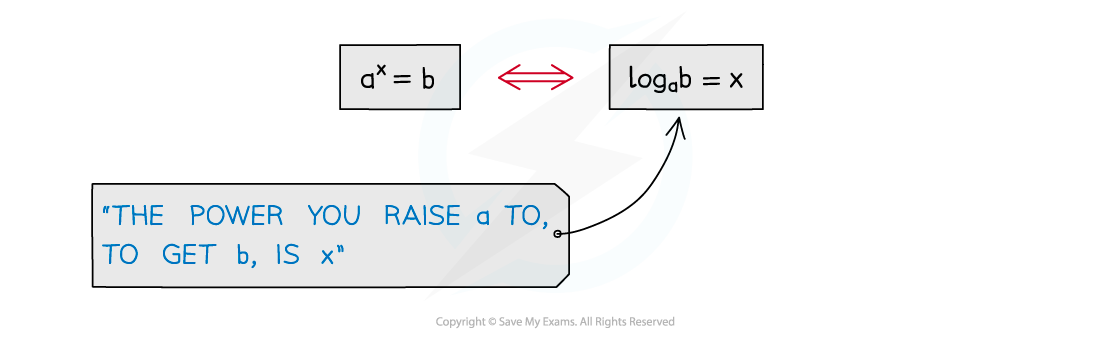
Laws of Logarithms Notes fig1, A Level & AS Maths: Pure revision notes

There are many laws or rules of indices, for example
- a^m x aⁿ = a^m+n
- (a^m)ⁿ = a^mn
There are equivalent laws of logarithms (for a > 0)
- $\log_{a} x y = \log_{a} x + \log_{a} y$
- $\log_{a} (\frac{x}{y}) = \log_{a} x - \log_{a} y$
- $\log_{a} x^{k} = k \log_{a} x$

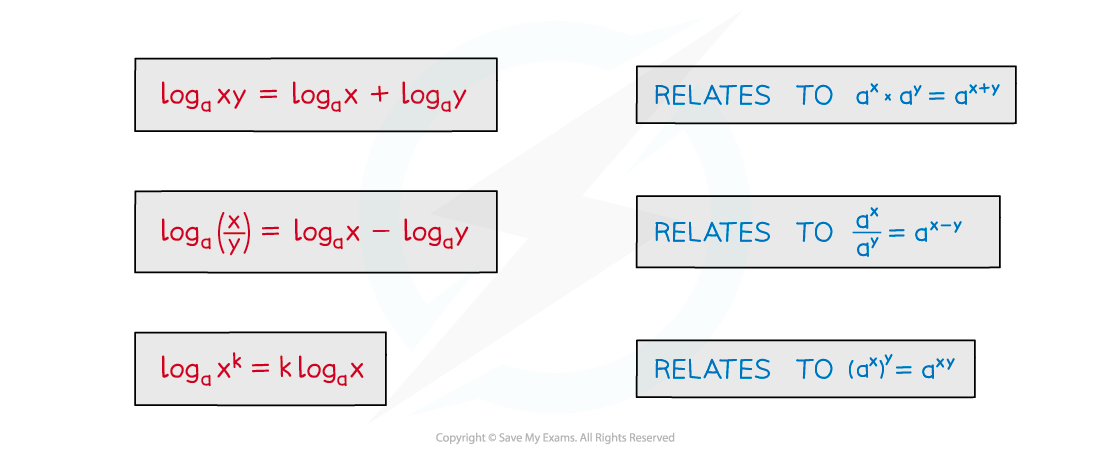
Laws of Logarithms Notes fig2, A Level & AS Level Pure Maths Revision Notes

There are also some particular results these lead to
- $\log_{a} a = 1$
- $\log_{a} a^{x} = x$
- $a^{\log_{a} x} = x$
- $\log_{a} 1 = 0$
- $\log_{a} (\frac{1}{x}) = - \log_{a} x$

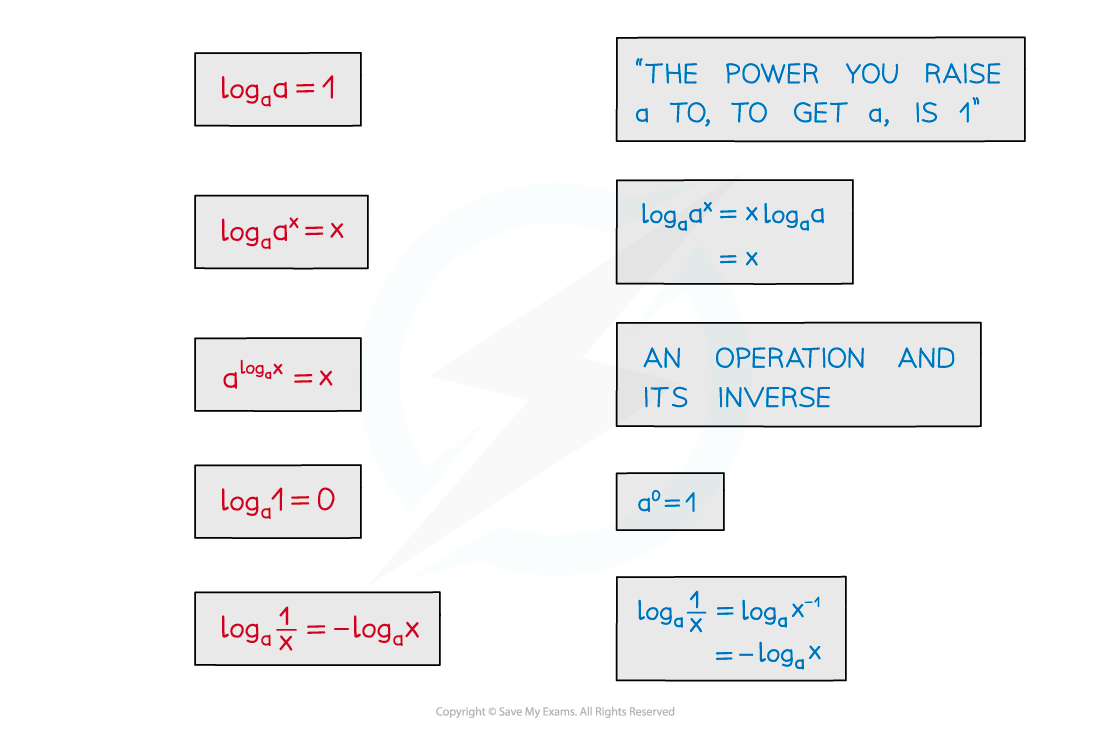
Laws of Logarithms Notes fig3, A Level & AS Level Pure Maths Revision Notes

Two of these were seen in the notes Logarithmic Functions
Beware …
- … log (x + y) ≠ log x + log y
Results apply to ln too
- $\ln x \equiv \log_{e} x$
- In particular $e^{\ln x} = x$ and $\ln (e^{x}) = x$

How do I use the laws of logarithms?

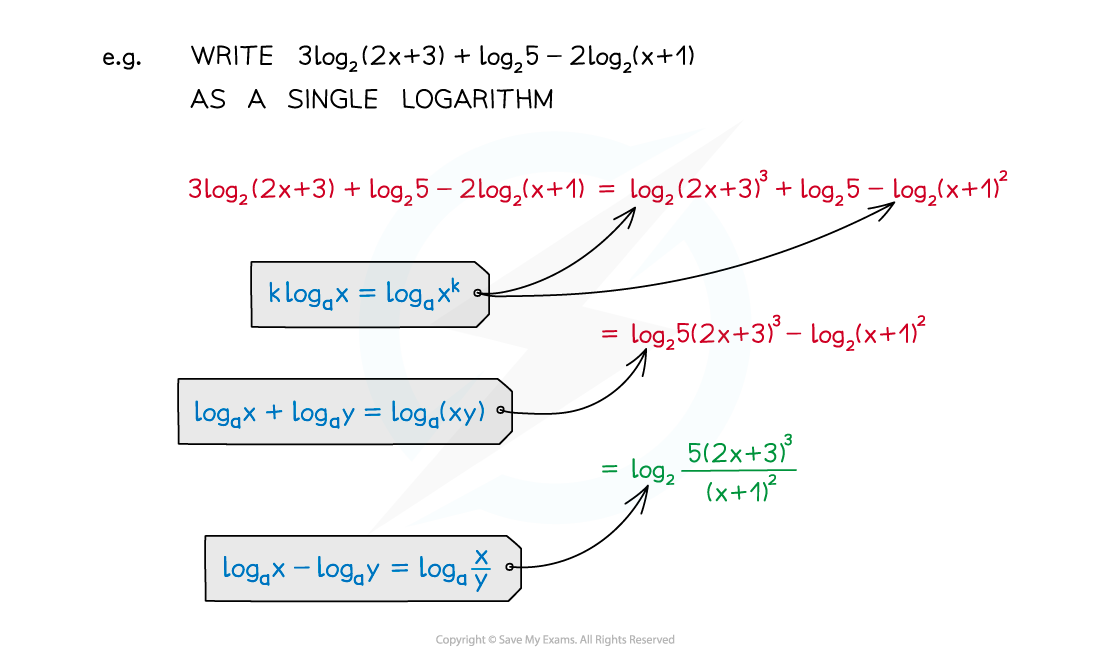
Laws of logarithms can be used to …
- … simplify expressions
- … solve logarithmic equations
- … solve exponential equations

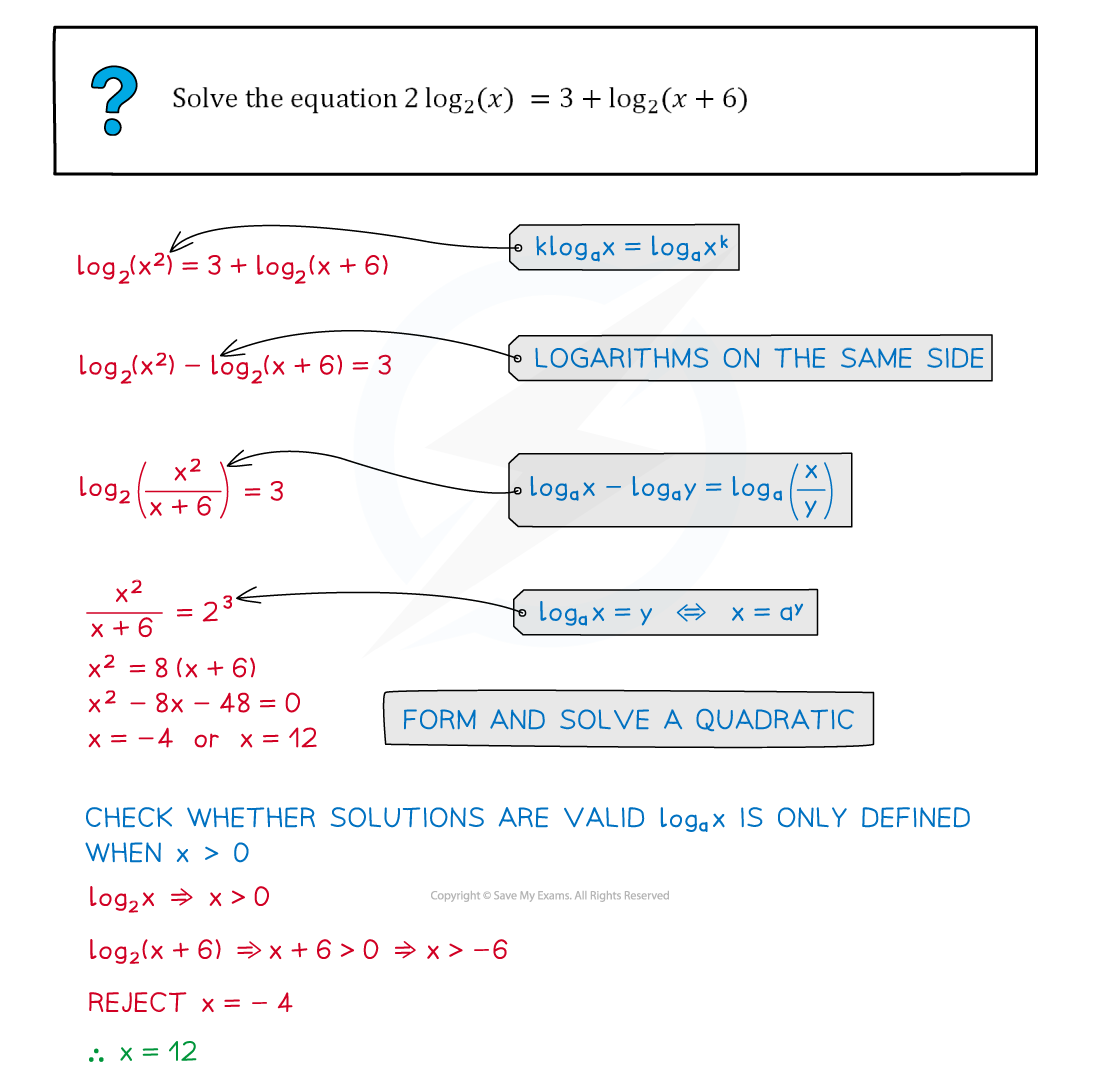
Examiner Tips and Tricks

Remember to check whether your solutions are valid. log (x+k) is only defined if x > -k.
You will lose marks if you forget to reject invalid solutions.

Worked Example

2-2-1-laws-of-logs-we-solution-1

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Did this page help you?

Previous:Derivatives of Exponential FunctionsNext:Exponential Equations