Derivatives of Exponential Functions (Cambridge (CIE) A Level Maths): Revision Note
Exam code: 9709
Did this video help you?
Derivatives of exponential functions
What is the derivative of ex?
y = ex has the particular property that
i.e. for every real number x, the gradient of y = ex is also equal to ex (see Derivatives of Exponential Functions)


e ≈ 2.718 (see "e")
Recall that the derivative is the gradient function for a curve (see First Principles Differentiation)
What is the derivative of y = ekx and y=e-kx?

The derivative of y = ekx is
The derivative of y = e-kx is
Examiner Tips and Tricks
Remember that (like π) e is a number.
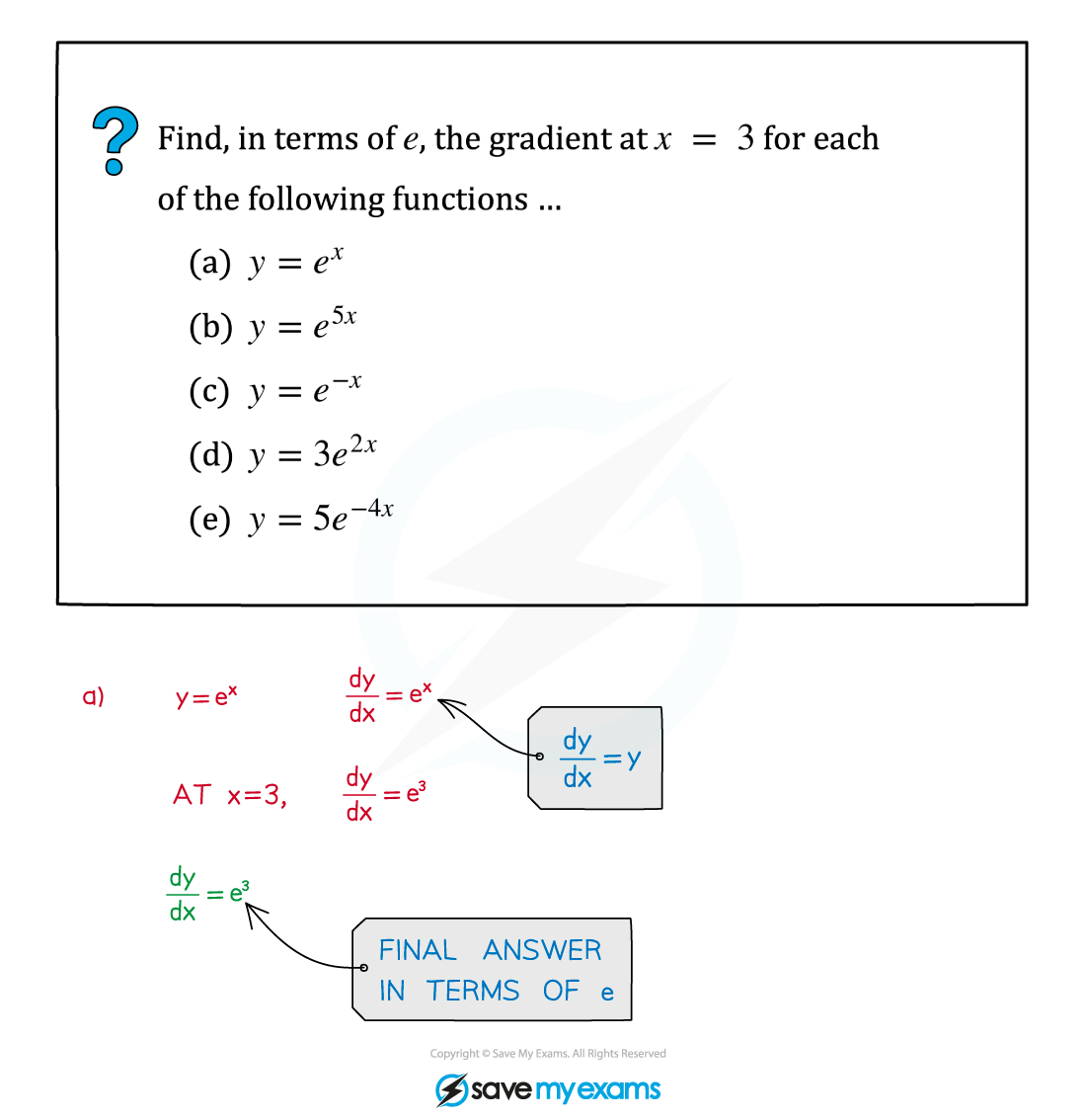
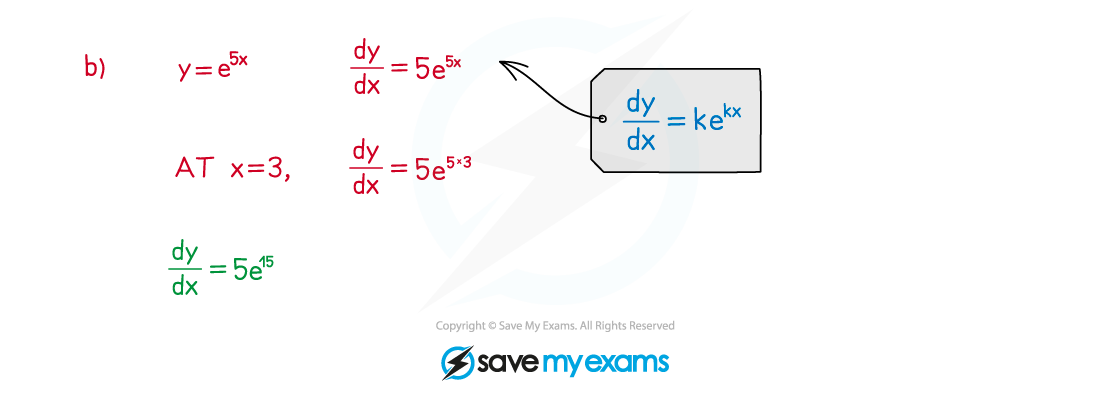
Exam questions can ask for answers to be given as exact values in terms of e (see the Worked Example below).
Worked Example


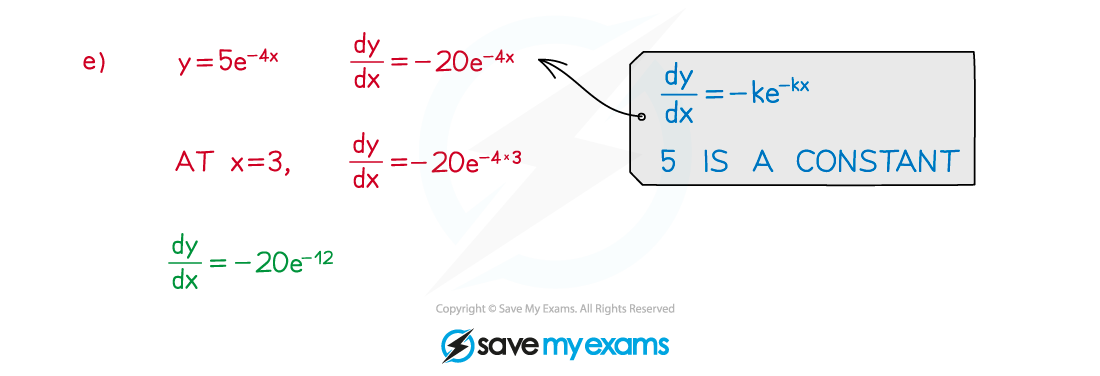

Unlock more, it's free!
Did this page help you?