Logarithmic Functions (Cambridge (CIE) A Level Maths): Revision Note
Exam code: 9709
Did this video help you?
Logarithmic functions
What are logarithmic functions?
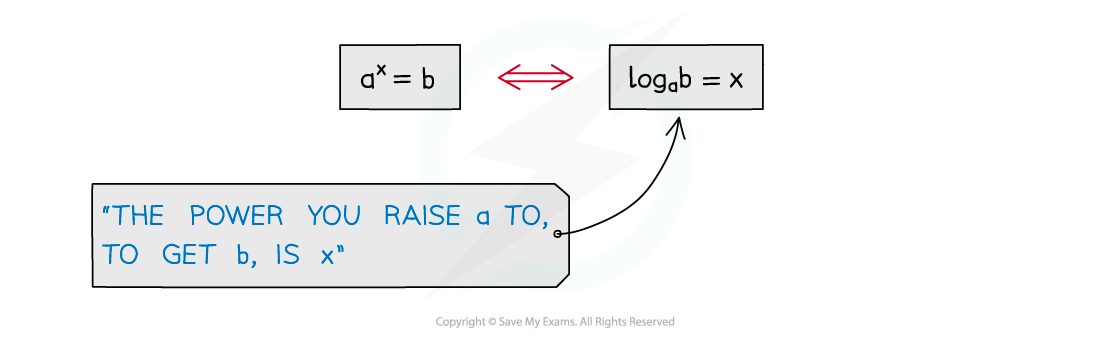
and
are equivalent statements
a > 0
a is called the base
Every time you write a logarithm statement say to yourself what it means
log3 81 = 4
“the power you raise 3 to, to get 81, is 4”
logp q = r
“the power you raise p to, to get q, is r”
How are logarithms and powers inverses of each other?
A logarithm is the inverse of raising to a power so we can use rules to simplify logarithmic functions

How do I use the inverse property of logs and powers?
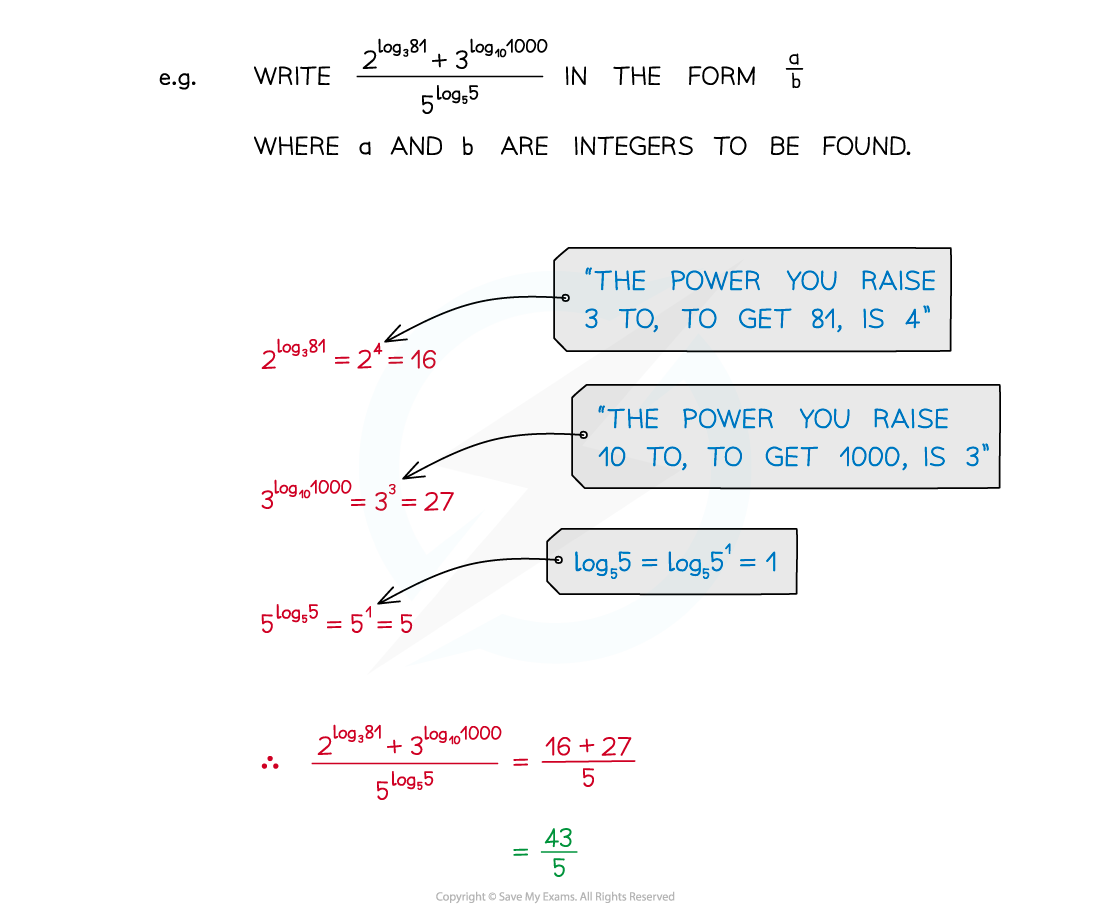
Recognising the rules of logarithms allows expressions to be simplified
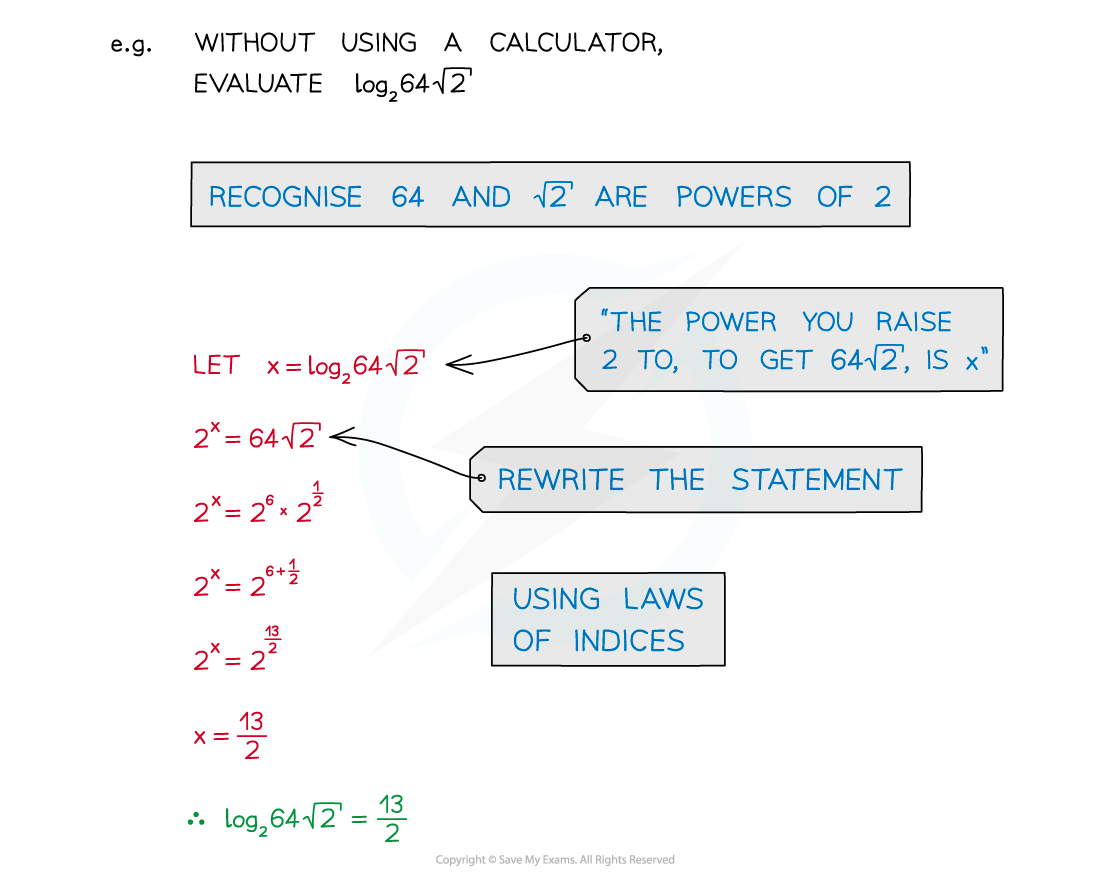
Recognition of common powers helps in simple cases
Powers of 2: 20 = 1, 21 = 2, 22 = 4, 23 = 8, 24 =16, …
Powers of 3: 30 = 1, 31 = 3, 32 = 9, 33 = 27, 34 = 81, …
The first few powers of 4, 5 and 10 should also be familiar
For more awkward cases a calculator is needed

Calculators can have, possibly, three different logarithm buttons

This button allows you to type in any number for the base

Natural logarithms (see “e”)

Shortcut for base 10 although SHIFT button needed
Before calculators, logarithmic values had to be looked up in printed tables
What notation is used with logarithms?
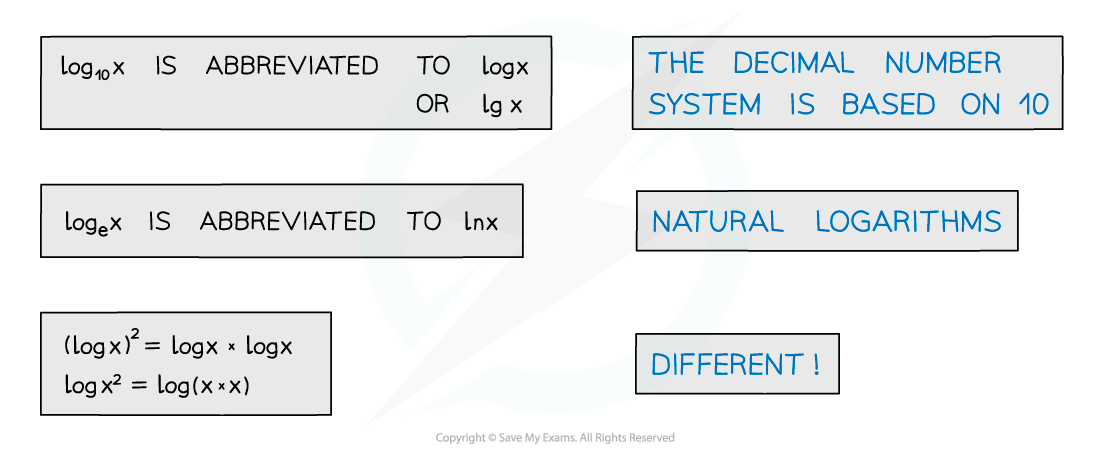
10 is a common base
log10 x is abbreviated to log x or lg x
The value e is another common base
loge x is abbreviated to ln x
(log x)2 ≠ log x2
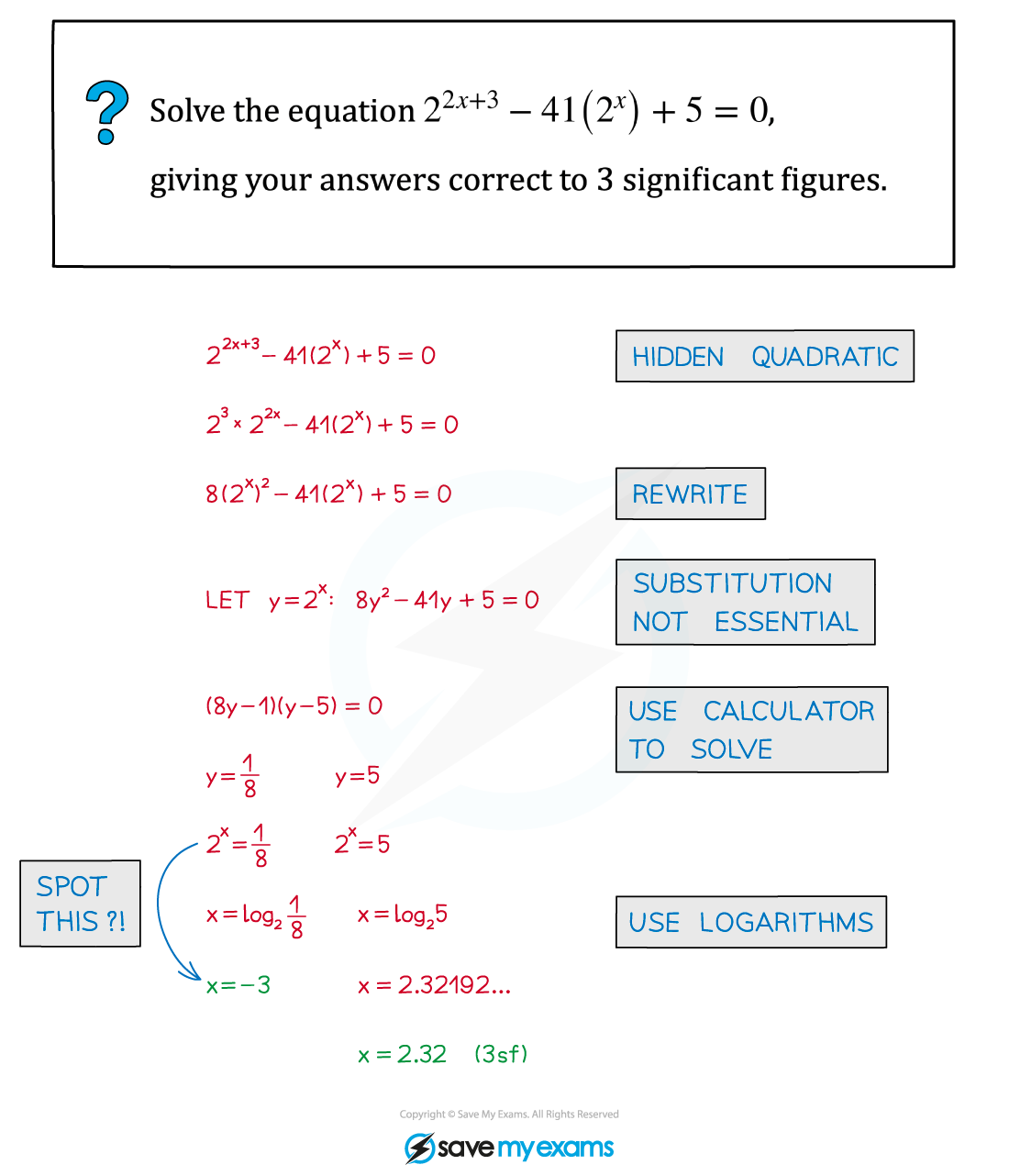
Worked Example

Unlock more, it's free!
Did this page help you?