A LevelMathsCambridge (CIE)Pure 3Revision NotesTrigonometryCompound & Double Angle FormulaeCompound Angle Formulae

Compound Angle Formulae (Cambridge (CIE) A Level Maths): Revision Note

Exam code: 9709

Roger B

Author

Roger B

Last updated

Cambridge (CIE) Maths: Pure 3OCR Maths A: PureAQA Maths: PureEdexcel Maths: Pure

Compound angle formulae

What are the compound angle formulae?

  • There are six compound angle formulae (also known as addition formulae), two each for sin, cos and tan:

  • For sin the +/- sign on the left-hand side matches the one on the right-hand side

sin left parenthesis A plus B right parenthesis identical to sin A cos B plus cos A sin B sin left parenthesis A minus B right parenthesis identical to sin A cos B minus cos A sin B

  • For cos the +/- sign on the left-hand side is opposite to the one on the right-hand side

cos left parenthesis A plus B right parenthesis identical to cos A cos B minus sin A sin B cos left parenthesis A minus B right parenthesis identical to cos A cos B plus sin A sin B

  • For tan the +/- sign on the left-hand side matches the one in the numerator on the right-hand side, and is opposite to the one in the denominator

tan left parenthesis A plus B right parenthesis identical to fraction numerator tan A plus tan B over denominator 1 minus tan A tan B end fraction tan left parenthesis A minus B right parenthesis identical to fraction numerator tan A minus tan B over denominator 1 plus tan A tan B end fraction

  • You can derive the tan identity by:

    • Writing tan left parenthesis A plus B right parenthesis identical to fraction numerator sin left parenthesis A plus B right parenthesis over denominator cos left parenthesis A plus B right parenthesis end fraction

    • Dividing the numerator and denominator by cos A cos B

Examiner Tips and Tricks

  • All these formulae are in the formulae booklet – you don't have to memorise them.

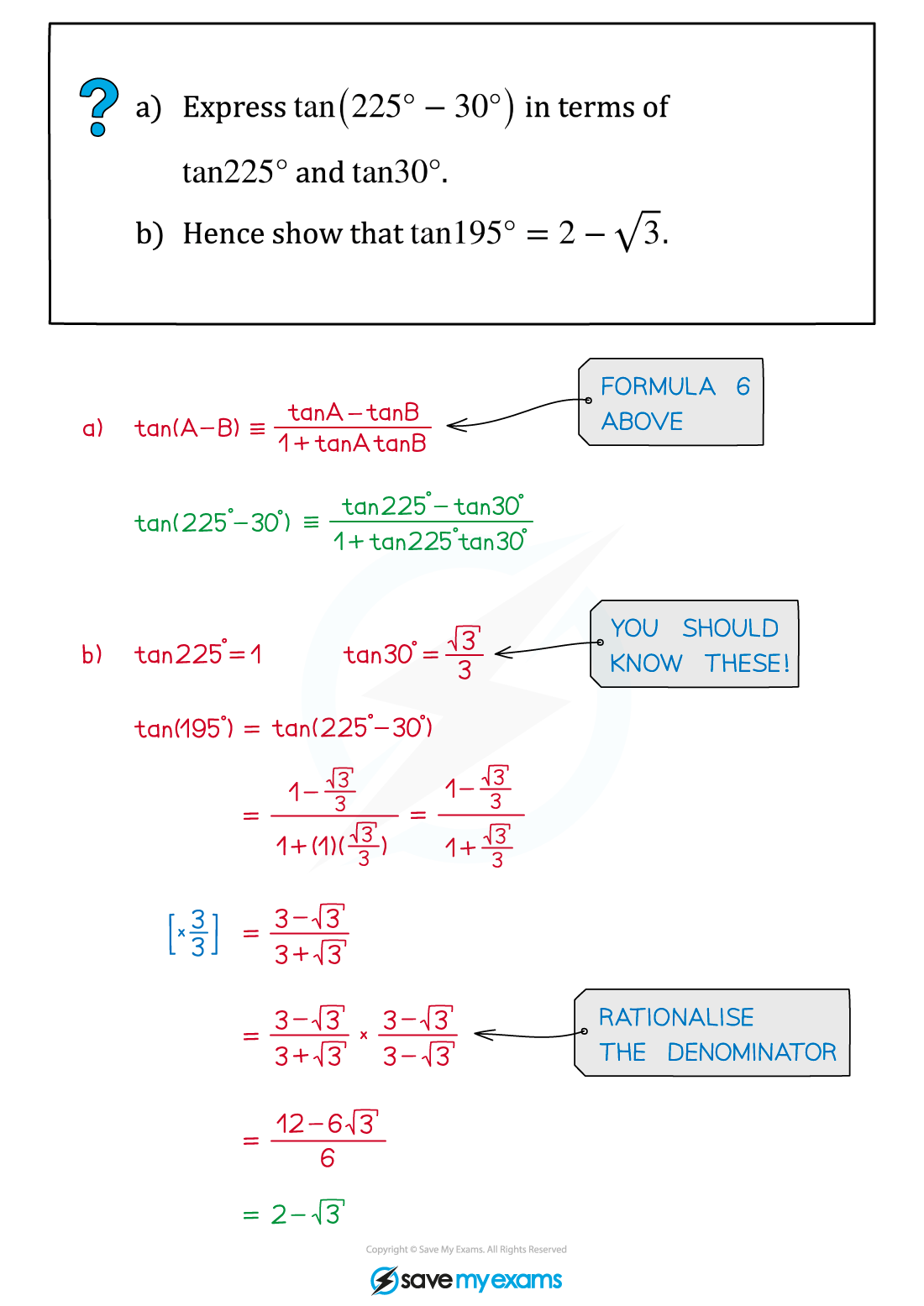
Worked Example

Comp Angle Forms Example, A Level & AS Maths: Pure revision notes
👀 You've read 1 of your 5 free revision notes this week
An illustration of students holding their exam resultsUnlock more revision notes. It’s free!

By signing up you agree to our Terms and Privacy Policy.

Already have an account? Log in

Test yourself
Previous:Identities with Reciprocal Trigonometric FunctionsNext:Double Angle Formulae
Roger B

Author: Roger B

Expertise: Maths Content Creator

Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

Download notes on Compound Angle Formulae