Rate Equation (HL) (DP IB Chemistry): Revision Note

Rate equation

• The rate of reaction can be found by measuring the:

  • Decrease in reactant concentration over time

  • Increase in product concentration over time

• The units for rate of reaction are mol dm^-3 s^-1

Rate of reaction

• The following general reaction will be used as an example to study the rate of reaction

D (aq) → E (aq) + F (g) 

• The rate of reaction at different concentrations of D is measured and tabulated

• Plotting the results on a graph shows a directly proportional relationship between the rate of reaction and concentration of D:

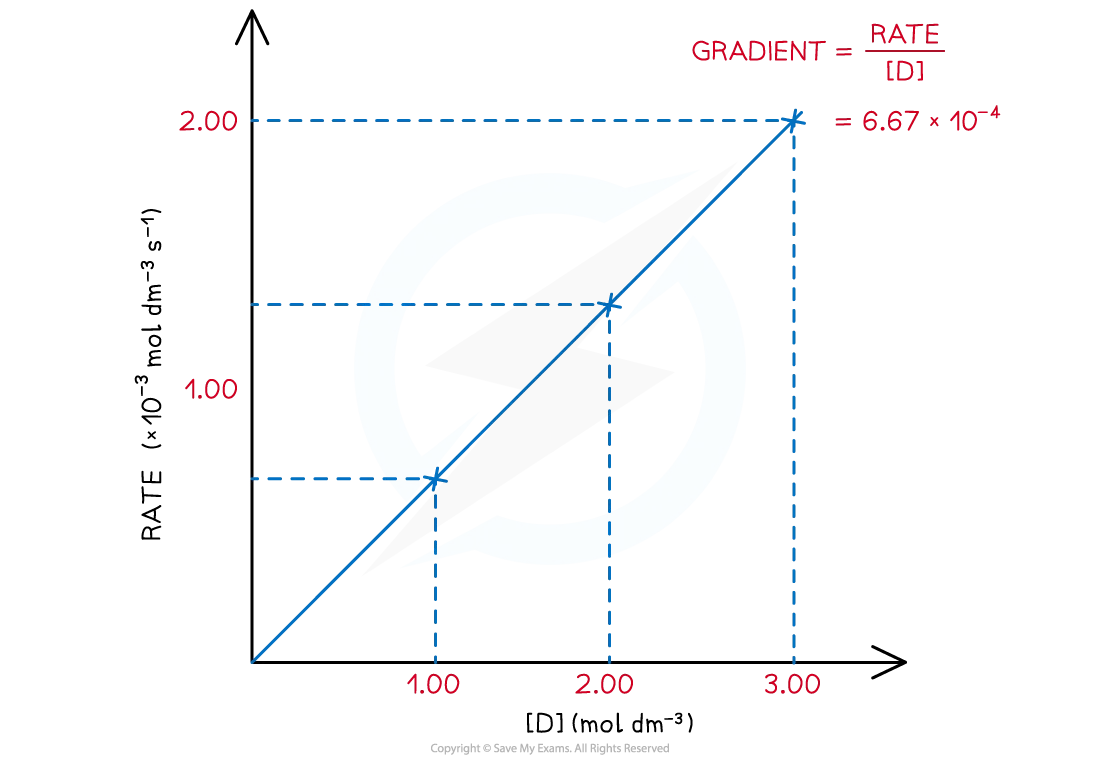
• The value of the gradient is constant as it is a straight line

• The gradient at each concentration is calculated by:

gradient =  

• This leads to the rate expression:

Rate ∝ [D]       or       Rate = k[D]

• This rate expression means that:

  • If the concentration of D doubles, then the rate doubles

  • If the concentration of D halves, then the rate halves

• Not all reactions show this directly proportional relationship between rate and reactant concentration

• The rate equation and orders of reaction help explain how rate is affected by each reactant

What is the rate equation?

• The rate equation expresses the relationship between reaction rate and species concentrations, usually in the form:

Rate = k [species 1] ^m [species 2]ⁿ

• In most reactions:

  • These species are reactants

  • But catalysts or products may also appear

  • Intermediates do not appear

• The following reaction will be used to discuss rate equations:

A (aq) + B (aq) → C (aq) + D (g) 

• The rate equation for this reaction is:

Rate of reaction = k [A]^m [B]ⁿ

• Where:

  • [A] and [B] are the concentrations of the reactants

  • m and n are orders with respect to each reactant

• Rate equations depend on the reaction mechanism

  • They must be determined experimentally

  • They cannot be found from the stoichiometric equations

What is the order of reaction?

• The order of reaction shows how the rate of a reaction depends on the concentration of a reactant

• It is the power to which the concentration is raised in the rate equation

• The order can be positive, negative, or fractional

  • Fractional orders suggest that the reaction involves multiple steps

Zero order

• When the order of reaction with respect to a reactant is 0:

  • Changing the concentration has no effect on the rate of reaction

  • The reactant does not appear in the rate equation

First order

• When the order of reaction with respect to a reactant is 1:

  • The rate is directly proportional to the concentration

    • Doubling the concentration doubles the rate

  • The reactant is included in the rate equation (no power shown)

Second order

• When the order of reaction with respect to a reactant is 2:

  • The rate is proportional to the square of the concentration

    • Doubling the concentration quadruples the rate

  • The reactant is included in the rate equation, squared

Overall order

• The overall order of reaction is the sum of the powers of the reactants in a rate equation:

Rate of reaction = k [A]^m [B]ⁿ

Overall order of reaction = m + n

How can the rate equation be deduced from experimental data?

• The following reaction will be used to determine the rate equation from experimental concentration and rate data:

(CH₃)₃CBr + OH^- → (CH₃)₃COH + Br^-

• The table below shows the concentrations of reactants and the initial rates of reaction under different conditions:

• To write the rate equation:

  • Determine the order with respect to each reactant

    • This can be done by analysing the table of concentration and rate data

  • Use the reaction equation to write an initial rate equation

  • Apply the orders of reactant to the initial rate equation

How to determine order from data

1. Choose two experiments where only one reactant changes in concentration

2. Calculate how the concentration changes

3. Calculate how the rate changes

4. Use this information to deduce the order of reaction with respect to that reactant

5. Repeat for the other reactant(s)

Order with respect to [(CH₃)₃CBr]

1. In experiments 1 and 2:

   • [(CH₃)₃CBr] changes

   • [OH^-] remains constant

2. The [(CH₃)₃CBr] doubles

   • Experiment 1 [(CH₃)₃CBr] = 1.0 x 10^-3 mol dm^-3

   • Experiment 2 [(CH₃)₃CBr] = 2.0 x 10^-3 mol dm^-3

3. The rate of the reaction doubles

   • Experiment 1 rate = 3.0 x 10^-3 mol dm^-3 s^-1

   • Experiment 2 rate = 6.0 x 10^-3 mol dm^-3 s^-1

4. The order with respect to [(CH₃)₃CBr] is 1 / first order

   • [Change in concentration]^order = change in rate

   • [2]^order = 2

   • [2]¹ = 2

Order with respect to [OH^–]

1. In experiments 1 and 3:

   • [OH^–] changes

   • [(CH₃)₃CBr] remains constant

2. The [OH^–] doubles

   • Experiment 1 [OH^–] = 2.0 x 10^-3 mol dm^-3

   • Experiment 3 [OH^–] = 4.0 x 10^-3 mol dm^-3

3. The rate of the reaction increases by a factor of 4

   • Experiment 1 rate = 3.0 x 10^-3 mol dm^-3 s^-1

   • Experiment 3 rate = 1.2 x 10^-2 mol dm^-3 s^-1

4. The order with respect to [OH^–] is 2 / second order

   • [Change in concentration]^order = change in rate

   • [2]^order = 4

   • [2]² = 4

Building the rate equation

• Now that both orders of reaction are known, we can write the full rate equation

• The initial rate equation is:

Rate = k [(CH₃)₃CBr]^(m) [OH^–]⁽ⁿ⁾

• The order with respect to [(CH₃)₃CBr] is 1 / first order

  • First order reactants are written as [X]

• The order with respect to [OH^–] is 2 / second order

  • Second order reactants are written as [X]²

• This gives the final rate equation:

Rate = k [(CH₃)₃CBr] [OH^–]²

• The reaction is:

  • First order with respect to (CH₃)₃CBr

  • Second order with respect to OH^-

  • Third order overall