Scatter Diagrams & Correlation (DP IB Applications & Interpretation (AI)): Revision Note
Did this video help you?
Scatter diagrams
What does bivariate data mean?
Bivariate data is data which is collected on two variables, and it is used to look at how one of the variables affects the other
Each data value from one variable will be paired with a data value from the other variable
The two variables are often related, but do not have to be
What is a scatter diagram?
A scatter diagram is a way of graphing bivariate data
One variable will be on the x axis and the other will be on the y axis
The variable that can be controlled in the data collection is known as the independent or explanatory variable
It is plotted on the x axis
The variable that is measured or discovered in the data collection is known as the dependent or response variable
It is plotted on the y axis
Scatter diagrams can contain outliers that do not follow the trend of the data
Examiner Tips and Tricks
If you use scatter diagrams in your Internal Assessment then be aware that finding outliers for bivariate data is different to finding outliers for univariate data.
(x, y) could be an outlier for the bivariate data even if x and y are not outliers for their separate univariate data sets.
Did this video help you?
Correlation
What is correlation?
Correlation is how the two variables change in relation to each other
Correlation could be the result of a causal relationship but this is not always the case
Linear correlation is when the changes are proportional to each other
Perfect linear correlation means that the bivariate data will all lie on a straight line on a scatter diagram
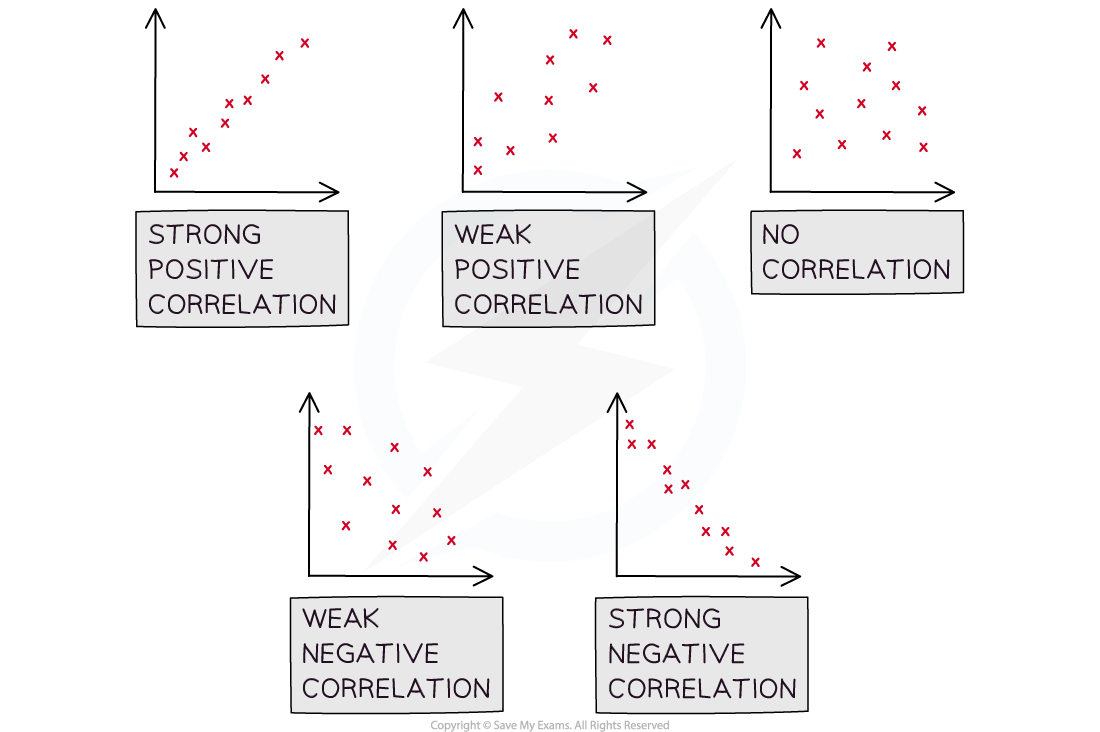
When describing correlation mention
The type of the correlation
Positive correlation is when an increase in one variable results in the other variable increasing
Negative correlation is when an increase in one variable results in the other variable decreasing
No linear correlation is when the data points don’t appear to follow a trend
The strength of the correlation
Strong linear correlation is when the data points lie close to a straight line
Weak linear correlation is when the data points are not close to a straight line
If there is strong linear correlation you can draw a line of best fit (by eye)
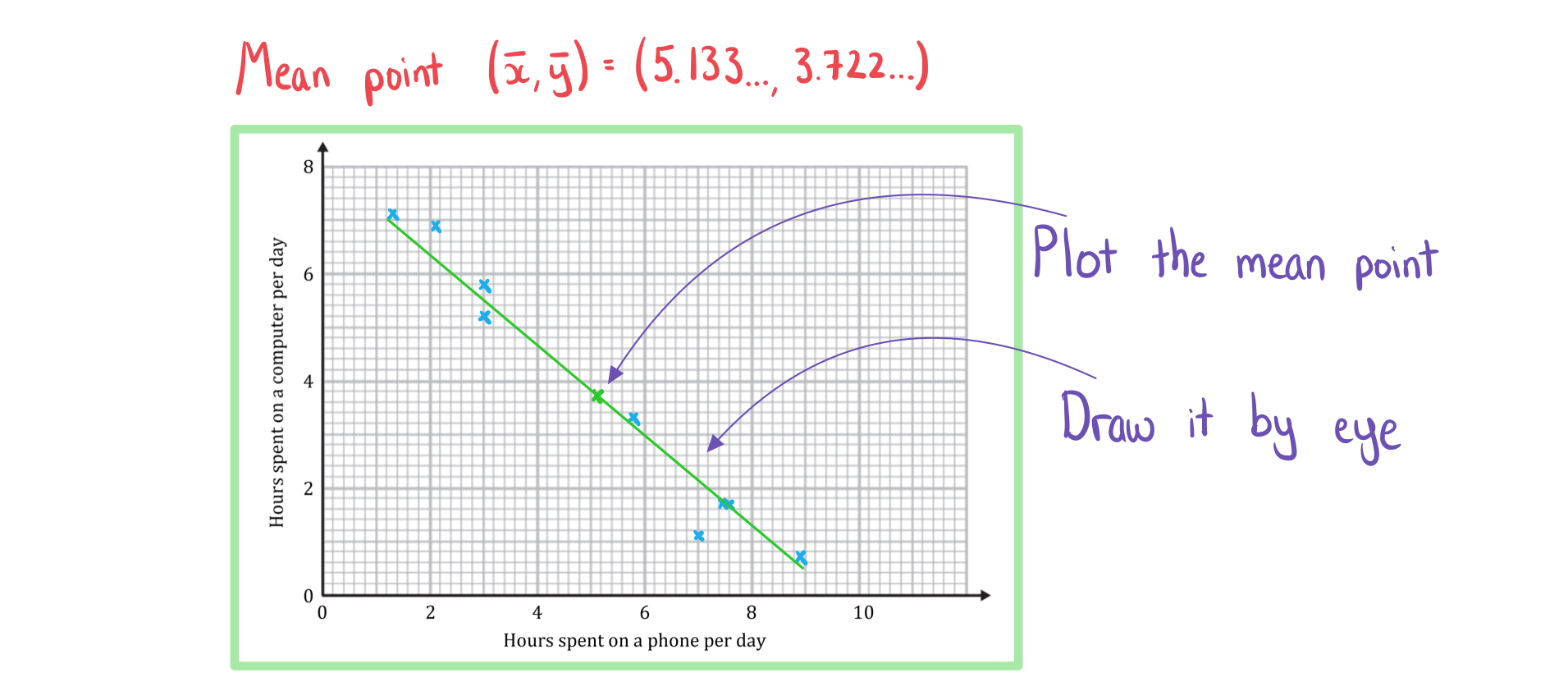
The line of best fit will pass through the mean point
is the mean of the set of
data values
is the mean of the set of
data values
If you are asked to draw a line of best fit
Plot the mean point
Draw a line going through it that follows the trend of the data
What is the difference between correlation and causation?
It is important to be aware that just because correlation exists, it does not mean that the change in one of the variables is causing the change in the other variable
Correlation does not imply causation!
If a change in one variable causes a change in the other then the two variables are said to have a causal relationship
Observing correlation between two variables does not always mean that there is a causal relationship
There could be underlying factors which is causing the correlation
Look at the two variables in question and consider the context of the question to decide if there could be a causal relationship
If the two variables are temperature and number of ice creams sold at a park then it is likely to be a causal relationship
Correlation may exist between global temperatures and the number of monkeys kept as pets in the UK but they are unlikely to have a causal relationship
Worked Example
A teacher is interested in the relationship between the number of hours her students spend on a phone per day and the number of hours they spend on a computer. She takes a sample of nine students and records the results in the table below.
Hours spent on a phone per day | 7.6 | 7.0 | 8.9 | 3.0 | 3.0 | 7.5 | 2.1 | 1.3 | 5.8 |
Hours spent on a computer per day | 1.7 | 1.1 | 0.7 | 5.8 | 5.2 | 1.7 | 6.9 | 7.1 | 3.3 |
a) Draw a scatter diagram for the data.
Answer:
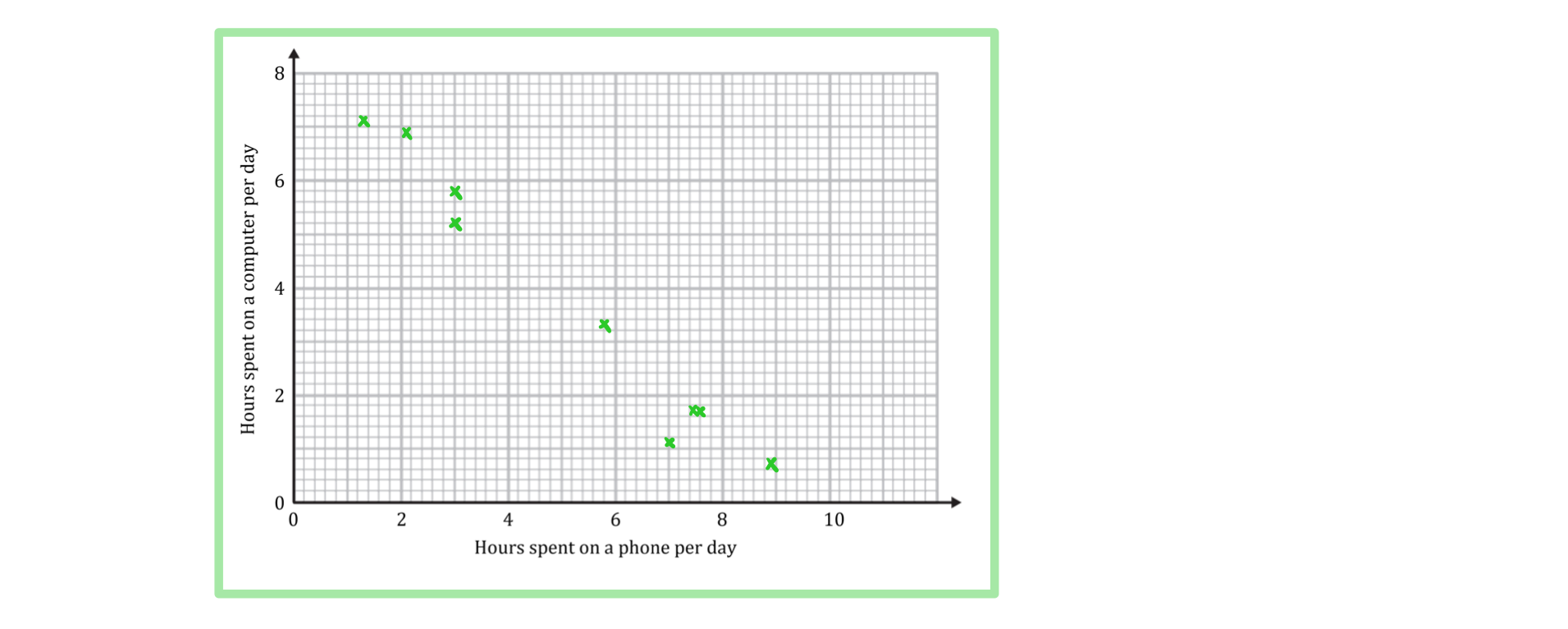
b) Describe the correlation.
Answer:

c) Draw a line of best fit.
Answer:

Unlock more, it's free!
Did this page help you?