Discriminants (DP IB Analysis & Approaches (AA)): Revision Note
Did this video help you?
Discriminants
What is the discriminant of a quadratic function?
The discriminant of a quadratic is denoted by the Greek letter
(upper case delta)
For the quadratic function
the discriminant is given by
This is given in the formula booklet
The discriminant is the expression that is square rooted in the quadratic formula
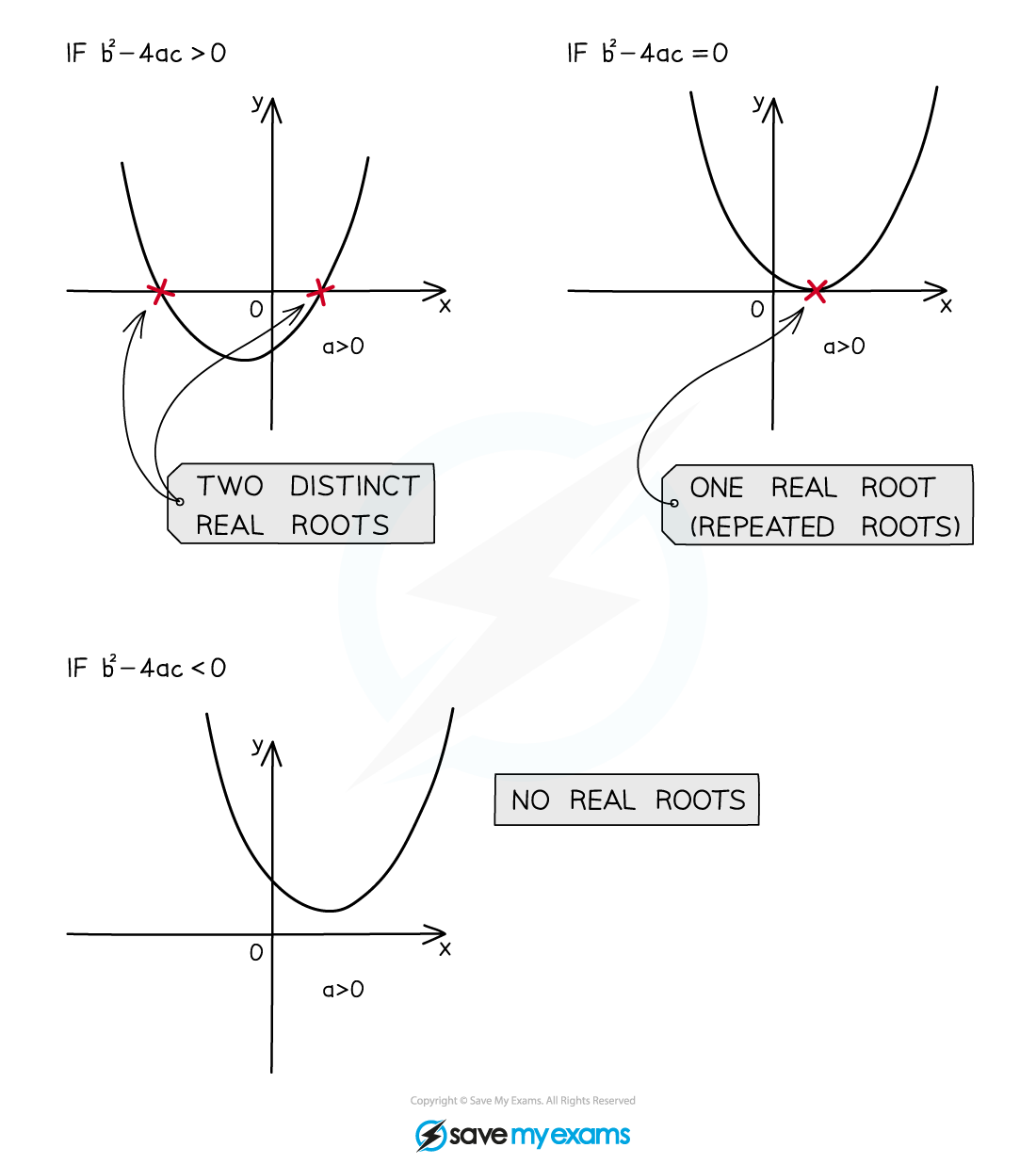
How does the discriminant of a quadratic function affect its graph and roots?
If
then
and
are two distinct values
The equation
has two distinct real solutions
The graph of
has two distinct real roots
This means the graph crosses the
-axis twice
If
then
and
are both zero
The equation
has one repeated real solution
The graph of
has one repeated real root
This means the graph touches the
-axis at exactly one point
This means that the
-axis is a tangent to the graph
If
then
and
are both undefined
The equation
has no real solutions
The graph of
has no real roots
This means the graph never touches the x-axis
This means that graph is wholly above (or wholly below) the
-axis
Forming equations and inequalities using the discriminant
A common question is to find an unknown coefficient in a quadratic
Questions usually use the letter
for the unknown constant
You will be given a fact about the quadratic such as:
The number of solutions of the equation
The number of roots of the graph
To find the value or range of values of
Find an expression for the discriminant using
Decide whether
,
or
If the question says there are real roots but does not specify how many then use
Solve the resulting equation or inequality to find the value(s) of
Examiner Tips and Tricks
Questions will rarely use the word discriminant so it is important to recognise when its use is required.
Look for a number of roots or solutions being stated, or how many times the graph of a quadratic function intercepts the -axis.
Be careful setting up inequalities that concern "two real roots" () as opposed to "two real distinct roots" (
).
Worked Example
A function is given by , where
is a constant. The graph of
has two distinct real roots.
(a) Show that .

(b) Hence find the set of possible values of .
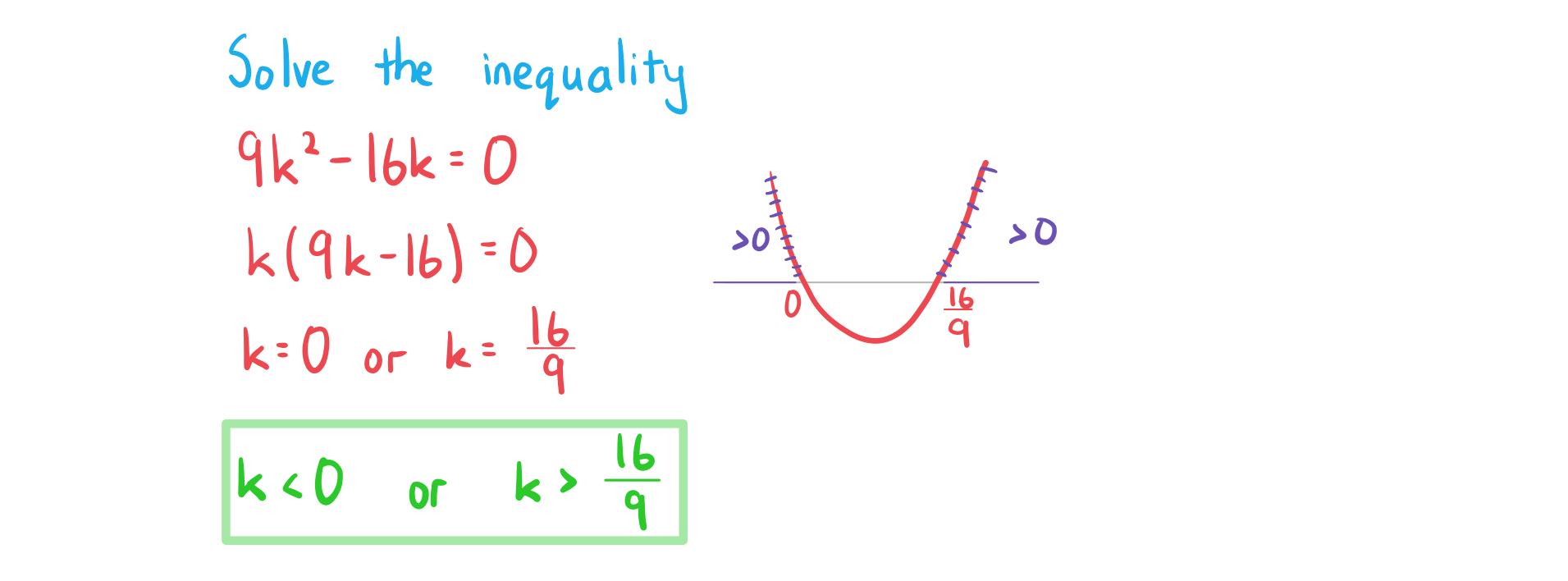

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?

