Revision NotesExam QuestionsFlashcardsPast PapersMock Exams
IBMathsDPApplications & Interpretation (AI)HLRevision Notes2. FunctionsTransformations of GraphsReflections of Graphs

Reflections of Graphs (DP IB Applications & Interpretation (AI)): Revision Note

Dan Finlay

Written by: Dan Finlay

Reviewed by: Mark Curtis

Updated on

DP Applications & Interpretation (AI): HLDP Analysis & Approaches (AA): HLDP Analysis & Approaches (AA): SL

Reflections of graphs

What are reflections of graphs?

  • A reflection is when

    • the graph is flipped about one of the coordinate axes

      • Its orientation changes

    • The size of the graph remains unchanged

  • A particular reflection is specified by an axis of symmetry about which you reflect

    • space y equals 0

      • This is the x-axis

    • space x equals 0

      • This is the y-axis

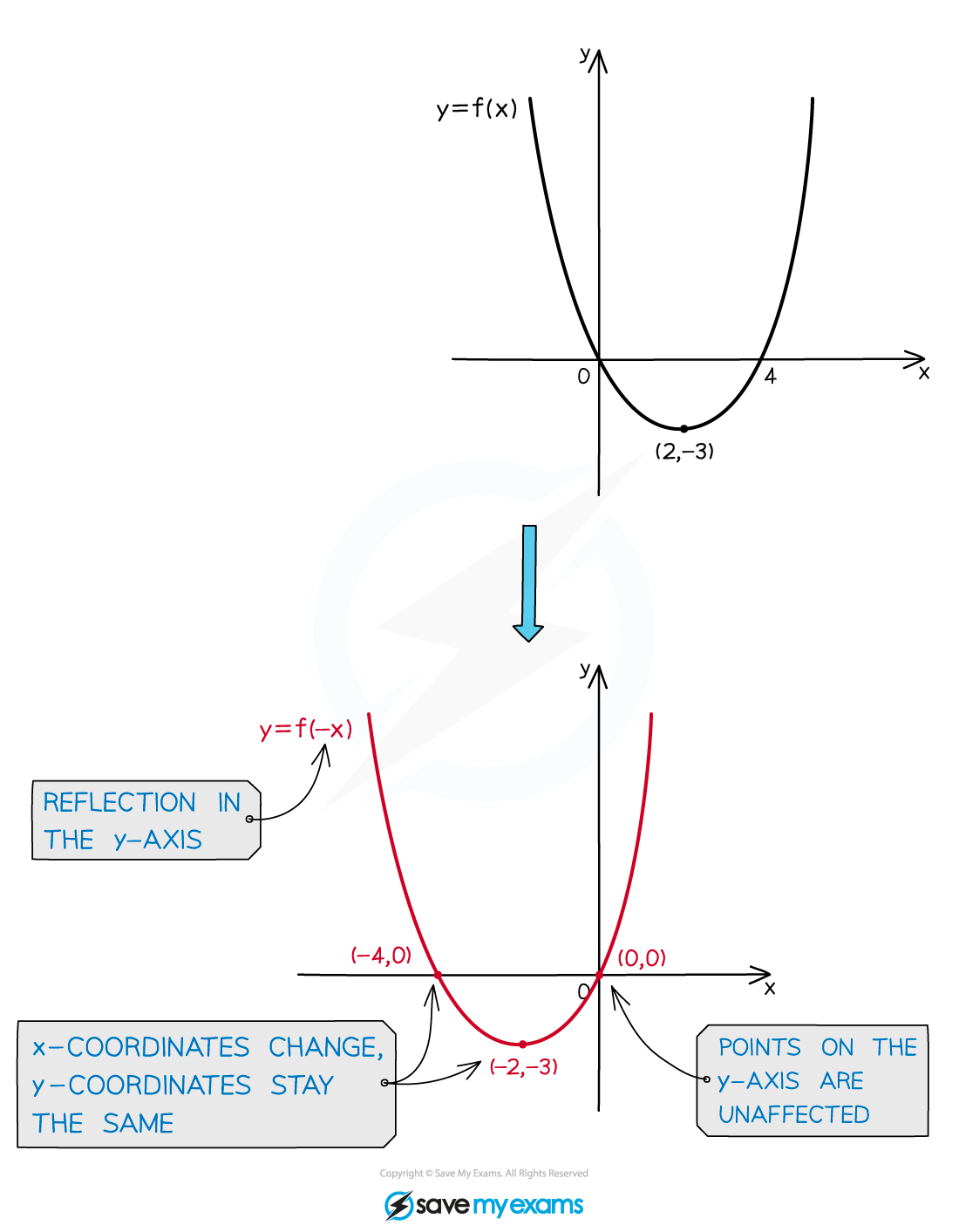
A graph showing a function reflected in the y-axis, where x-coordinates change, but y-coordinates remain the same.

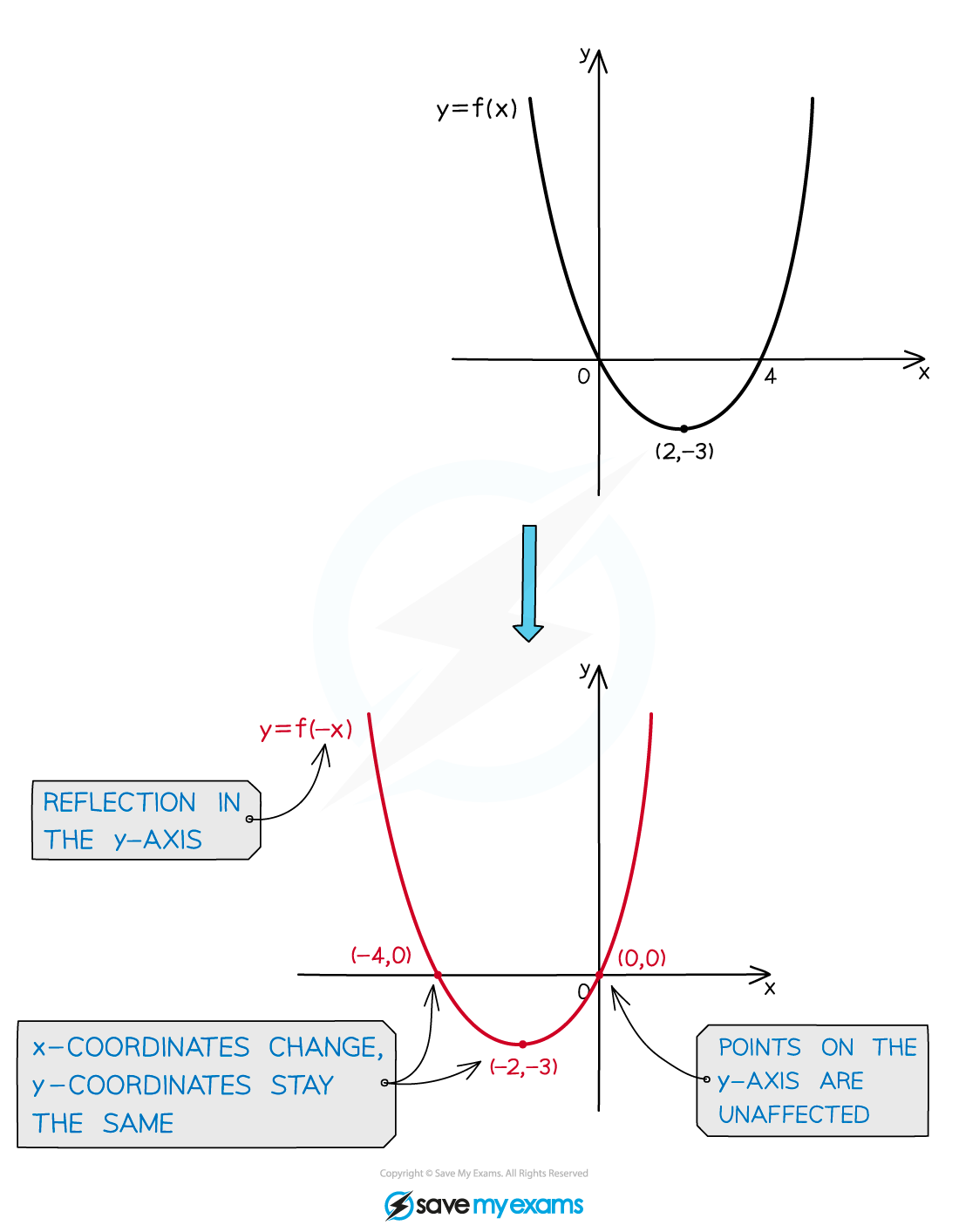
How do I find the graph equation after a reflection in the y-axis?

  • A horizontal reflection of the graph y equals f left parenthesis x right parenthesis about the y-axis is represented by the equation

    • y equals f left parenthesis negative x right parenthesis

    • Any vertical asymptotes change

      • x equals k becomes x equals negative k

      • Horizontal asymptotes stay the same

Graph showing function y=f(x) reflected in the y-axis to y=f(-x) with x-coordinates reflected and y-coordinates unchanged.

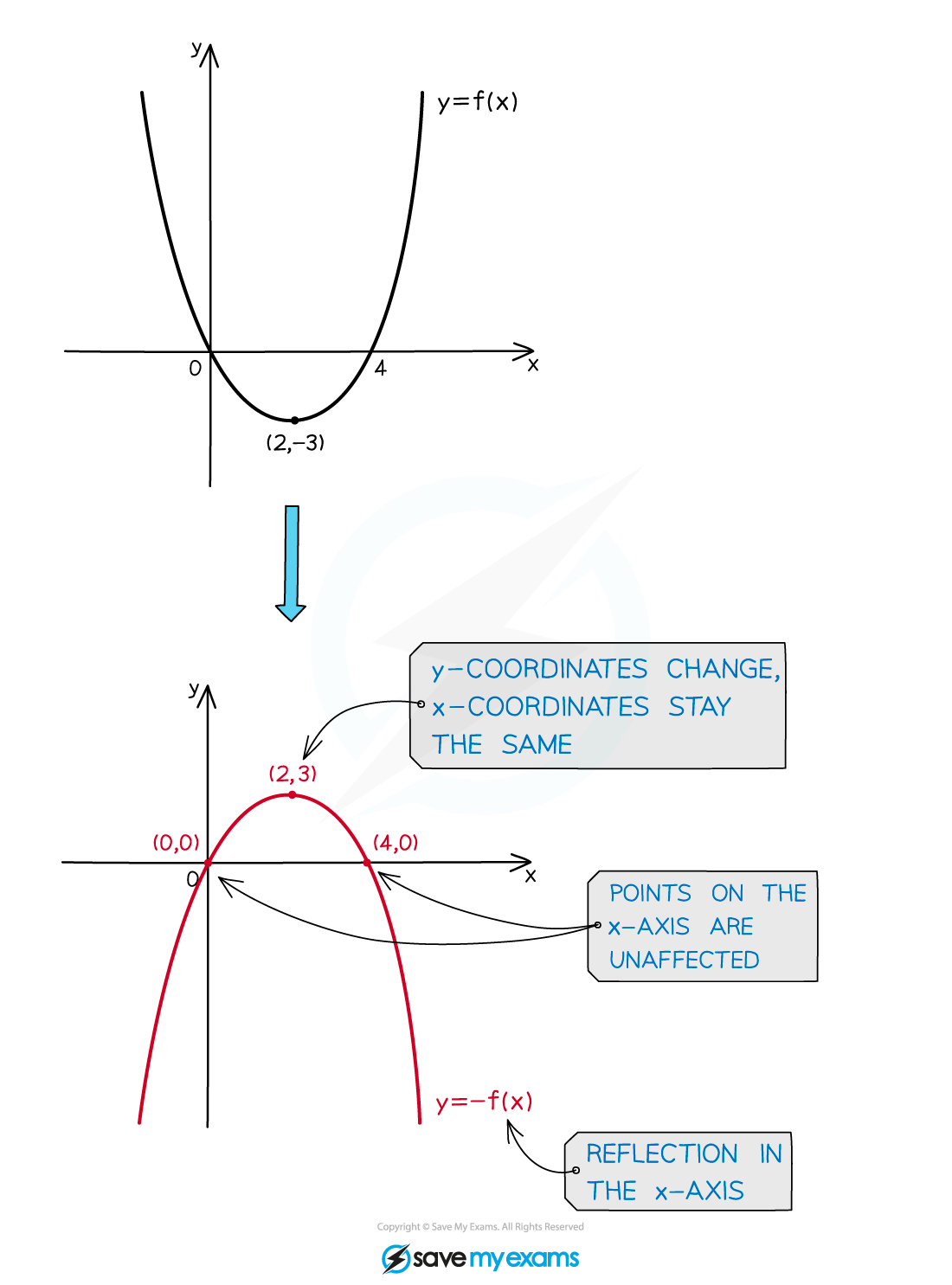
How do I find the graph equation after a reflection in the x-axis?

  • A vertical reflection of the graph y equals f left parenthesis x right parenthesis about the x-axis is represented by the equation

    • y equals negative f left parenthesis x right parenthesis

    • Any horizontal asymptotes change

      • space y equals k becomes space y equals negative k

      • Vertical asymptotes stay the same

Graph showing function y=f(x) reflected in the x-axis to y=-f(x), highlighting changes in y-coordinates, unchanged x-coordinates, and unaffected x-axis intercepts.

Worked Example

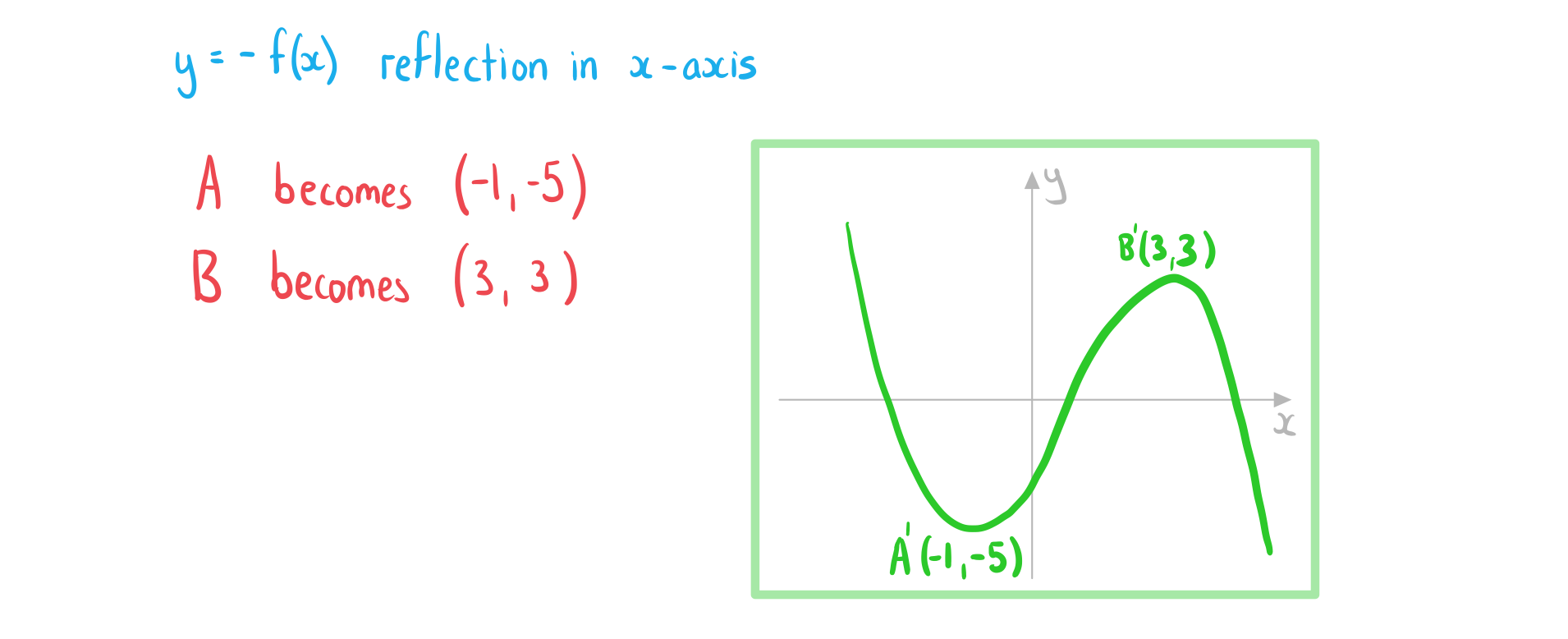
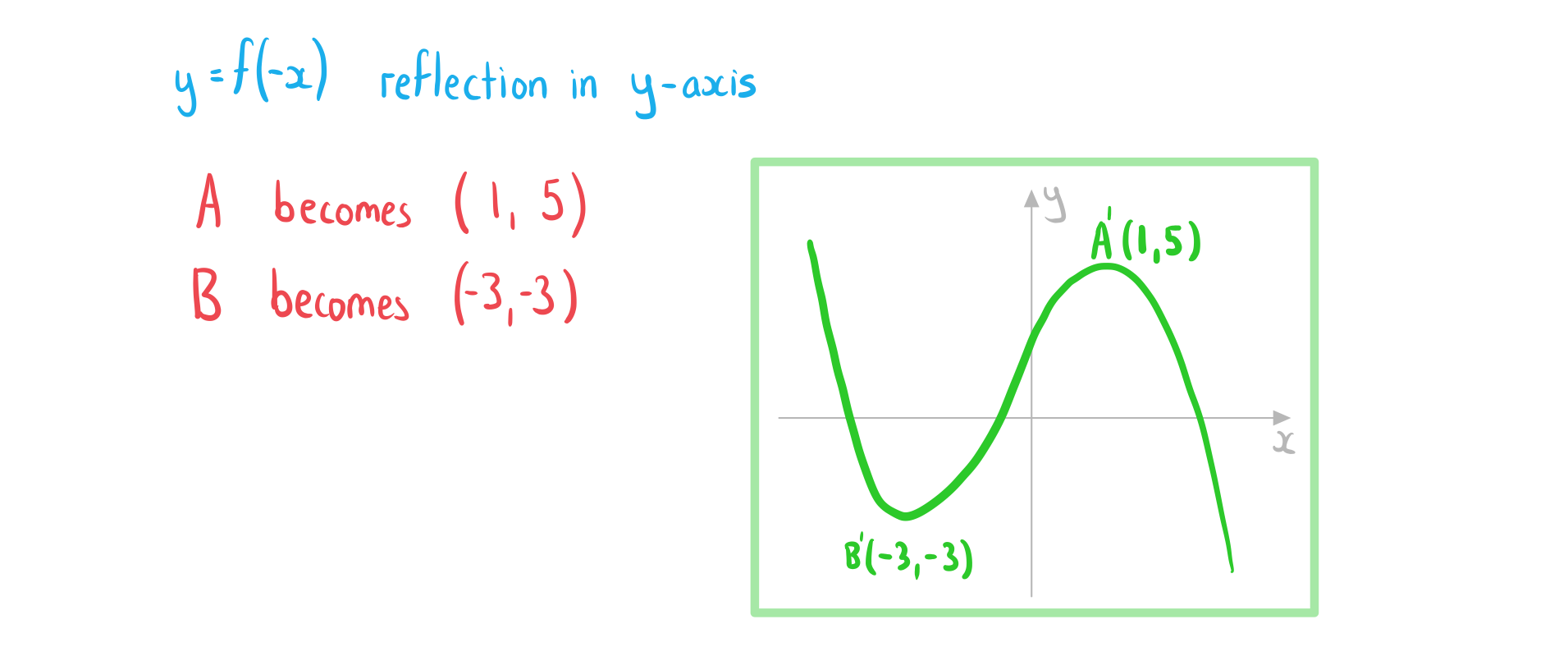
The diagram below shows the graph of y equals f left parenthesis x right parenthesis.

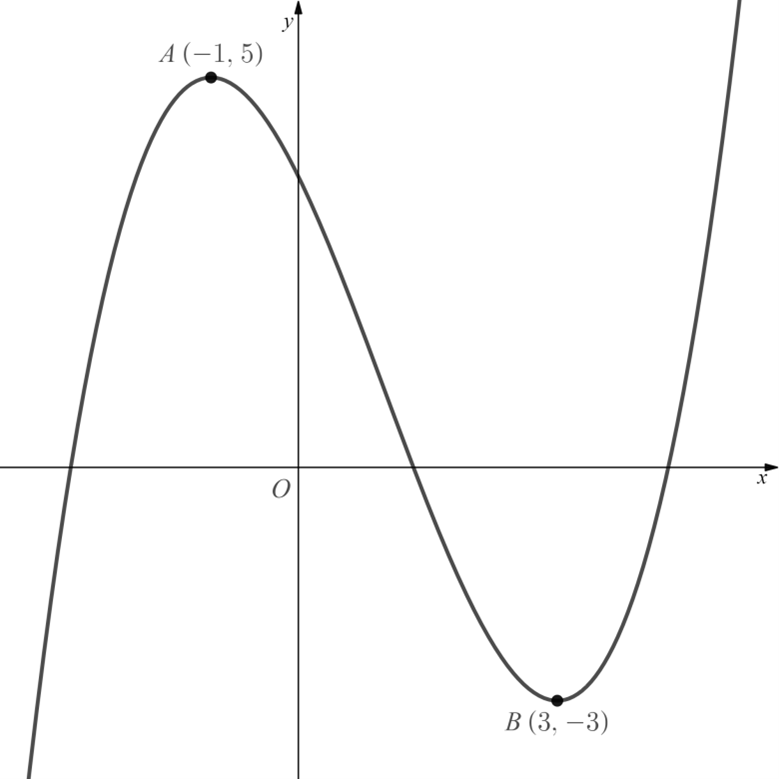
we-image

(a) Sketch the graph of y equals negative f left parenthesis x right parenthesis.

2-5-2-ib-aa-sl-reflect-graph-a-we-solution

(b) Sketch the graph of y equals f left parenthesis negative x right parenthesis.

2-5-2-ib-aa-sl-reflect-graph-b-we-solution

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards
    Previous:Translations of GraphsNext:Stretches of Graphs
    Author
    Reviewer
    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

    Mark Curtis

    Reviewer: Mark Curtis

    Expertise: Maths Content Creator

    Mark graduated twice from the University of Oxford: once in 2009 with a First in Mathematics, then again in 2013 with a PhD (DPhil) in Mathematics. He has had nine successful years as a secondary school teacher, specialising in A-Level Further Maths and running extension classes for Oxbridge Maths applicants. Alongside his teaching, he has written five internal textbooks, introduced new spiralling school curriculums and trained other Maths teachers through outreach programmes.