Graphs of Trigonometric Functions (DP IB Applications & Interpretation (AI)): Revision Note
Did this video help you?
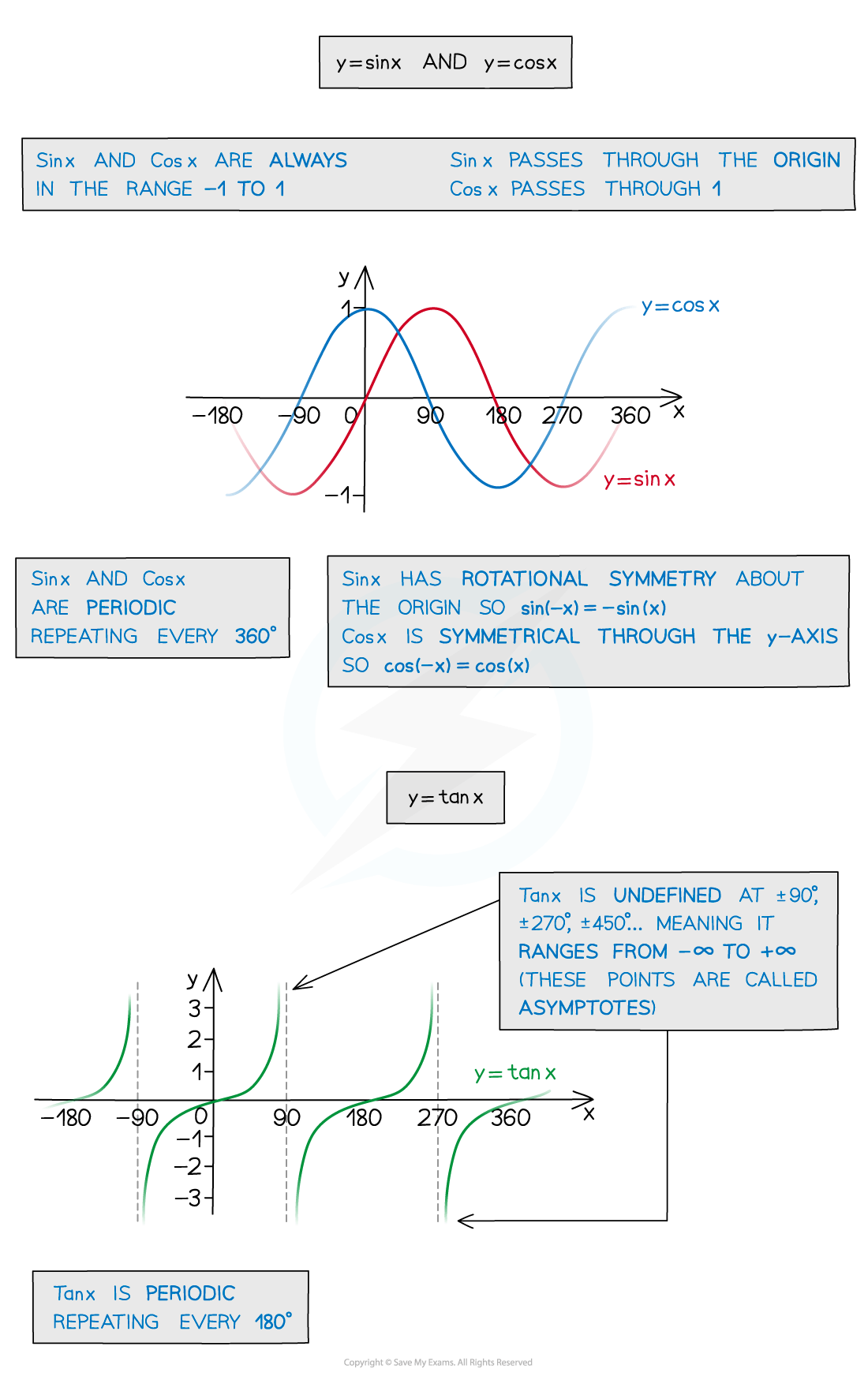
Graphs of trigonometric functions
What are the properties of the graphs of y = sin x and y = cos x?
The graphs of sin x and cos x are very similar
They are transformations of each other
They intersect the y-axis at different places
sin x passes through the origin
cos x passes through (0, 1)
Both graphs have the same domain and range
Domain:
Range:
The graphs are both periodic
They repeat every 360° (2π radians)
The amplitude of the graphs of sin x and cos x is 1
What are the properties of the graph of y = tan x?
The graph of tan x intersects the y-axis at the origin
The graph is undefined at the points ± 90°, ± 270° etc
There are asymptotes at these points on the graph
In radians this is at the points ±
, ±
etc
The domain and range of the graph is
Domain:
Range:
The graph of tan x is periodic
It repeats every 180° (π radians)
How do I sketch trigonometric graphs?
STEP 1
Check whether you are working in degrees or radiansCheck the domain given for this
STEP 2
Label the x-axis in multiples of 90° (or)
Make sure you cover the whole domain on the x-axis
STEP 3
Label the y-axisUse – 1 ≤ y ≤ 1 for sin or cos
Use the whole y-axis for tan
STEP 4
Identify what happens at each multiple of 90° (or)
sin0=0, cos0=1, tan0=0
sin90=1, cos90=0, tan90 is undefined
etc
STEP 5
Draw the graph using the general shape
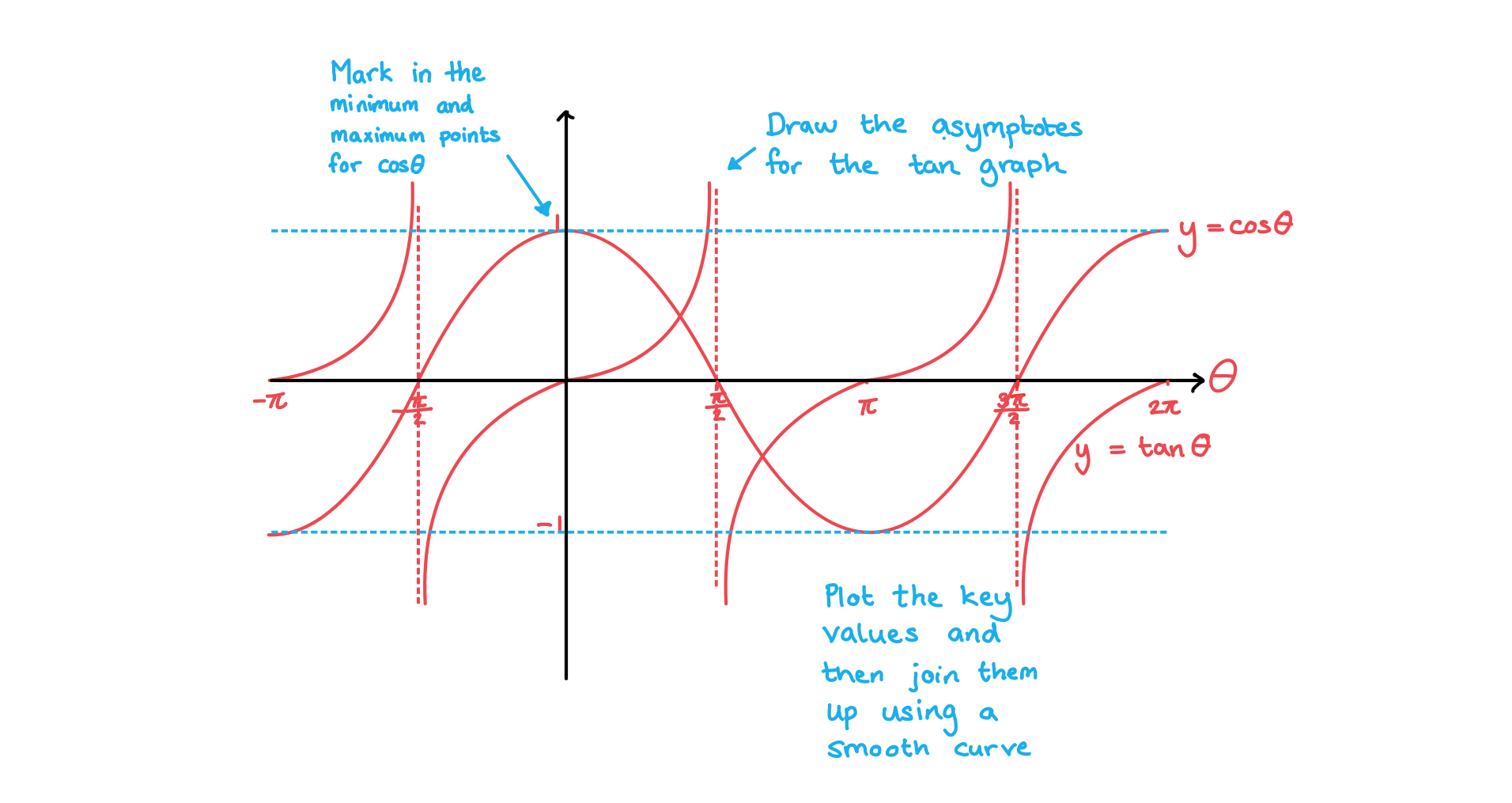
Worked Example
Sketch the graphs of and
on the same set of axes in the interval
. Clearly mark the key features of both graphs.
Answer:

Unlock more, it's free!
Was this revision note helpful?