Spearman's Rank Correlation Coefficient (DP IB Applications & Interpretation (AI)): Revision Note
Did this video help you?
Spearman’s rank
What is Spearman’s rank correlation coefficient?
Spearman's rank correlation coefficient is a measure of how well the relationship between two variables can be described using a monotonic function
A function is monotonic if it is either always increasing or always decreasing
i.e. if the
values are always increasing or always decreasing as the
values increase
This can be used as a way to measure correlation in linear models
Though Spearman's Rank correlation coefficient can also be used to assess a non-linear relationship
Each data is ranked, from biggest to smallest or from smallest to biggest
For n data values, they are ranked from 1 to n
It doesn't matter whether variables are ranked from biggest to smallest or smallest to biggest, but they must be ranked in the same order for both variables
Spearman’s rank of a sample is denoted by
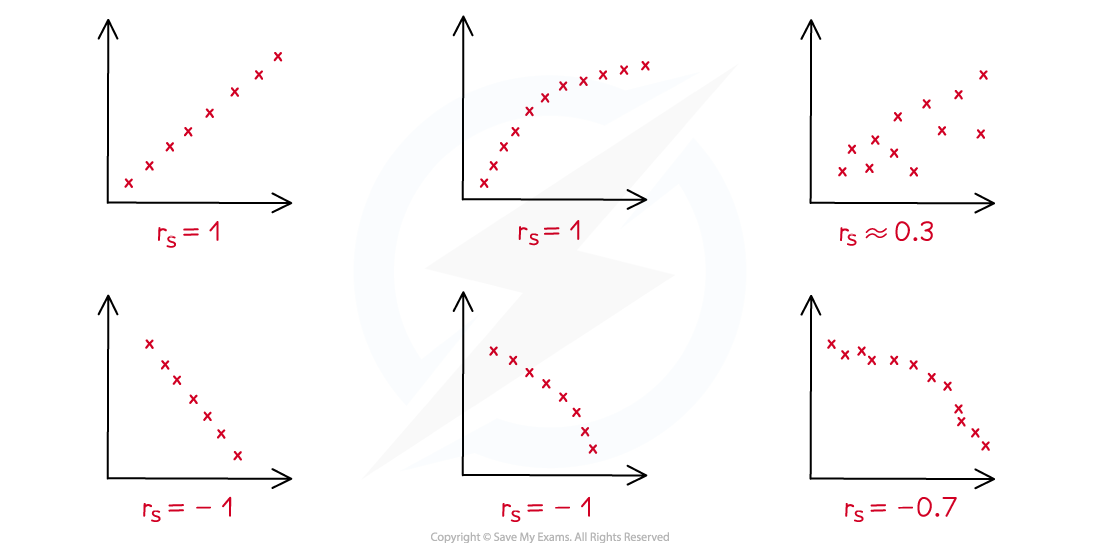
rs can take any value in the interval
A positive value of rs describes a degree of agreement between the rankings
A negative value of rs describes a degree of disagreement between the rankings
rs = 0 means the data shows no monotonic behaviour
rs = 1 means the rankings are in complete agreement: the data is strictly increasing
An increase in one variable always means an increase in the other
rs = -1 means the rankings are in complete disagreement: the data is strictly decreasing
An increase in one variable always means a decrease in the other
The closer to 1 or -1 the stronger the correlation of the rankings
How do I calculate Spearman’s rank correlation coefficient (PMCC)?
Rank each set of data independently
1 to n for the x-values
1 to n for the y-values
If some values are equal then give each the average of the ranks they would occupy
For example: if the 3rd, 4th and 5th highest values are equal then give each the ranking of 4
Calculate the PMCC of the rankings using your GDC
This value is Spearman's rank correlation coefficient
Worked Example
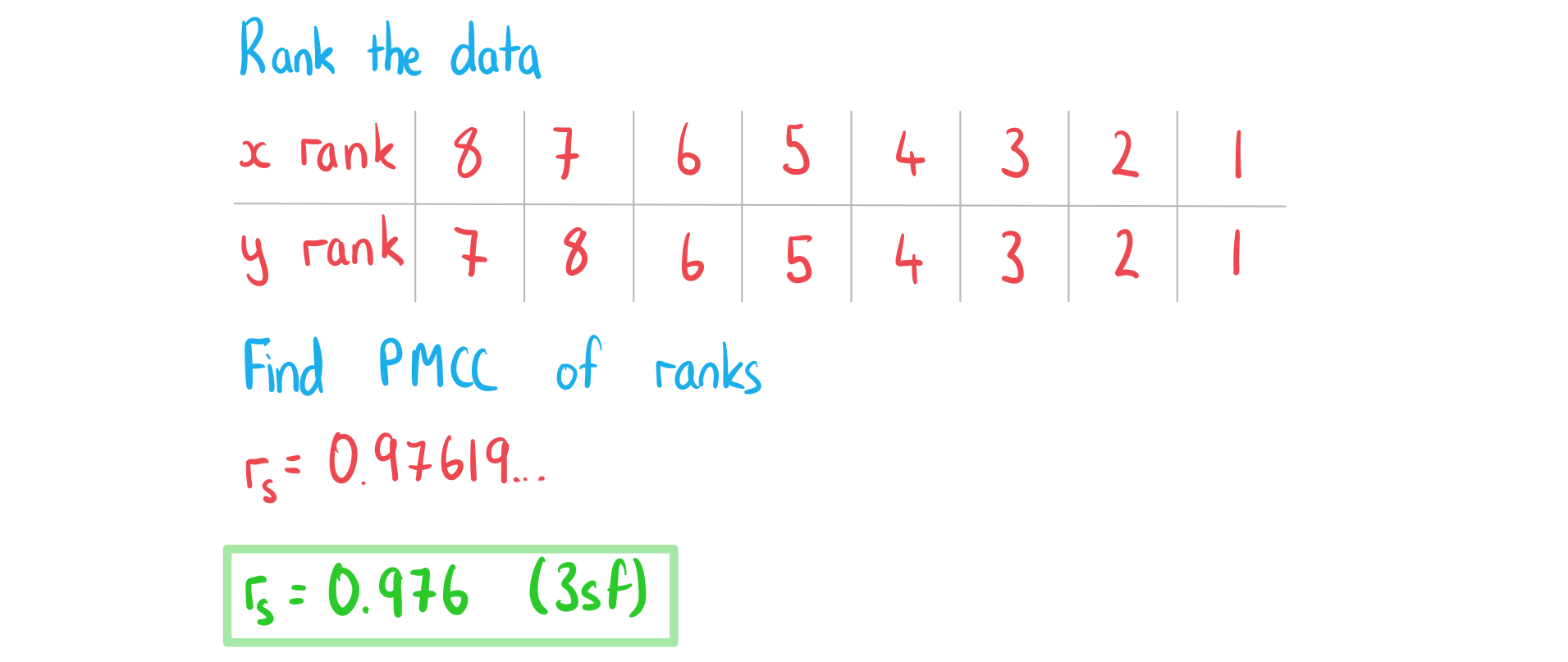
The table below shows the scores of eight students for a maths test and an English test.
Maths | 7 | 18 | 37 | 52 | 61 | 68 | 75 | 82 |
English | 5 | 3 | 9 | 12 | 17 | 41 | 49 | 97 |
a) Write down the value of Pearson’s product-moment correlation coefficient, .
Answer:

b) Find the value of Spearman’s rank correlation coefficient, .
Answer:
c) Comment on the values of the two correlation coefficients.
Answer:


Unlock more, it's free!
Was this revision note helpful?