Revision NotesExam QuestionsFlashcardsPast PapersMock Exams
IBMathsDPApplications & Interpretation (AI)HLRevision Notes4. Statistics & ProbabilityProbabilityTree Diagrams

Tree Diagrams (DP IB Applications & Interpretation (AI)): Revision Note

Dan Finlay

Written by: Dan Finlay

Reviewed by: Roger B

Updated on

DP Applications & Interpretation (AI): HLDP Analysis & Approaches (AA): HLDP Analysis & Approaches (AA): SLDP Applications & Interpretation (AI): SLDP Applications & Interpretation (AI): HLDP Applications & Interpretation (AI): SLDP Analysis & Approaches (AA): HLDP Analysis & Approaches (AA): SL

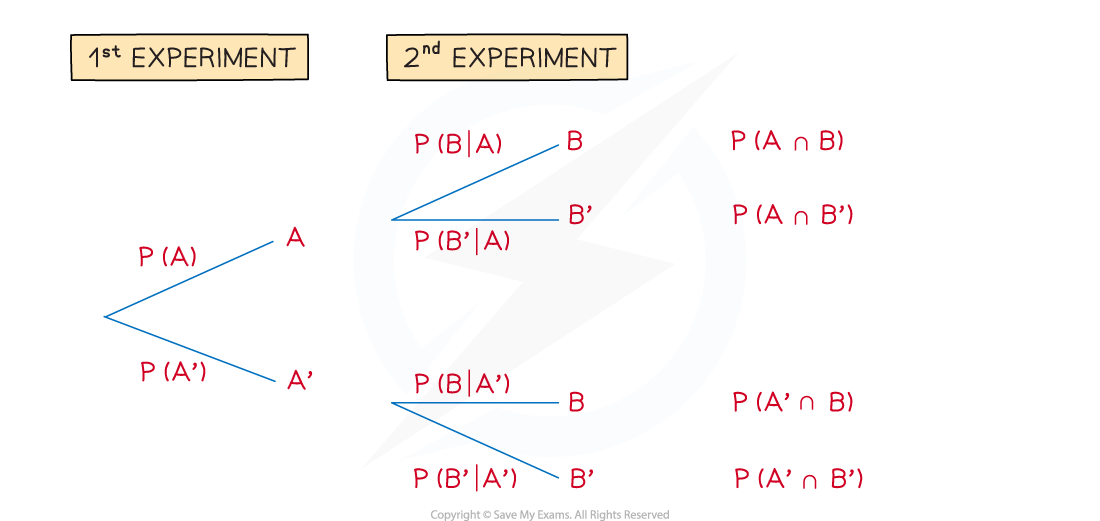
Tree diagrams

What is a tree diagram?

  • A tree diagram is another way to show the outcomes of combined events

    • They are very useful for intersections of events

  • The events on the branches must be mutually exclusive

    • Usually they are an event and its complement

  • The probabilities on the second sets of branches can depend on the outcome of the first event

    • These are conditional probabilities

  • When selecting the items from a bag:

    • The second set of branches will be the same as the first if the items are replaced

    • The second set of branches will be the different to the first if the items are not replaced

How are probabilities calculated using a tree diagram?

  • To find the probability that two events happen together you multiply the corresponding probabilities on their branches

    • It is helpful to find the probability of all combined outcomes once you have drawn the tree

  • To find the probability of an event you can:

    • add together the probabilities of the combined outcomes that are part of that event

      • For example: straight P left parenthesis A union B right parenthesis equals straight P left parenthesis A intersection B right parenthesis plus straight P left parenthesis A intersection B apostrophe right parenthesis plus straight P left parenthesis A apostrophe intersection B right parenthesis

    • subtract the probabilities of the combined outcomes that are not part of that event from 1

      • For example: straight P left parenthesis A union B right parenthesis equals 1 minus straight P left parenthesis A apostrophe intersection B apostrophe right parenthesis

Probability tree diagram showing two experiments with branches for events and probabilities. P(A) and P(A') are labelled along the first set of branches, and P(B|A), P(B'|A), P(B|A') and P(B'|A') are labelled along the second set of branches. Final combined probabilities P(A∩B), P(A∩B'), P(A'∩B) and P(A'∩B') are indicated at the far right.

Do I have to use a tree diagram?

  • If there are multiple events or trials then a tree diagram can get big

  • You can break down the problem by using the words AND/OR/NOT to help you find probabilities without a tree

  • You can speed up the process by only drawing parts of the tree that you are interested in

Which events do I put on the first branch?

  • If the events A and B are independent then the order does not matter

  • If the events A and B are not independent then the order does matter

    • If you have the probability of A given B then put B on the first set of branches

    • If you have the probability of B given A then put A on the first set of branches

Examiner Tips and Tricks

In an exam do not waste time drawing a full tree diagram for scenarios with lots of events unless the question asks you to. Only draw the parts that you are interested in.

For example, consider tokens drawn from a bag with red, purple, green, blue and yellow tokens in it. If you are only interested in the probabilities of drawing red tokens, then only draw branches for 'red' and 'not red', instead of branches for every single colour.

Worked Example

20% of people in a company wear glasses. 40% of people in the company who wear glasses are right-handed. 50% of people in the company who don’t wear glasses are right-handed.

a) Draw a tree diagram to represent the information.

4-3-3-ib-ai-aa-sl-tree-diagram-a-we-solution

b) One of the people in the company is randomly selected. Find the probability that the person is right-handed.

4-3-3-ib-ai-aa-sl-tree-diagram-b-we-solution

c) Given that a person who is right-handed is selected at random, find the probability that the person wears glasses.

4-3-3-ib-ai-aa-sl-tree-diagram-c-we-solution

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself
    Previous:Venn DiagramsNext:Discrete Probability Distributions
    Author
    Reviewer
    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

    Roger B

    Reviewer: Roger B

    Expertise: Maths Content Creator

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.