Probability & Types of Events (DP IB Applications & Interpretation (AI)): Revision Note
Did this video help you?
Probability basics
What key words and terminology are used with probability?
An experiment is a repeatable activity that has a result that can be observed or recorded
Trials are what we call the repeats of the experiment
An outcome is a possible result of a trial
An event is an outcome or a collection of outcomes
Events are usually denoted with capital letters: A, B, etc
n(A) is the number of outcomes that are included in event A
An event can have one or more than one outcome
A sample space is the set of all possible outcomes of an experiment
This is denoted by U
n(U) is the total number of outcomes
It can be represented as a list or a table
How do I calculate basic probabilities?
If all outcomes are equally likely then probability for each outcome is the same
Probability for each outcome is
Theoretical probability of an event can be calculated without using an experiment by dividing the number of outcomes of that event by the total number of outcomes
This is given in the formula booklet
Identifying all possible outcomes either as a list or a table can help
Experimental probability (also known as relative frequency) of an outcome can be calculated using results from an experiment by dividing its frequency by the number of trials
Relative frequency of an outcome is
How do I calculate the expected number of occurrences of an outcome?
Theoretical probability can be used to calculate the expected number of occurrences of an outcome from n trials
If the probability of an outcome is p and there are n trials then:
The expected number of occurrences is np
This does not mean that there will exactly np occurrences
If the experiment is repeated multiple times then we expect the number of occurrences to average out to be np
What is the complement of an event?
The probabilities of all the outcomes add up to 1
Complementary events are when there are two events and exactly one of them will occur
One event has to occur but both events can not occur at the same time
The complement of event A is the event where event A does not happen
This can be thought of as not A
This is denoted A'
This is in the formula booklet
It is commonly written as
What are different types of combined events?
The intersection of two events (A and B) is the event where both A and B occur
This can be thought of as A and B
This is denoted as
The union of two events (A and B) is the event where A or B or both occur
This can be thought of as A or B
This is denoted
The event where A occurs given that event B has occurred is called conditional probability
This can be thought as A given B
This is denoted
How do I find the probability of combined events?
The probability of A or B (or both) occurring can be found using the formula
This is given in the formula booklet
You subtract the probability of A and B both occurring because it has been included twice (once in P(A) and once in P(B) )
The probability of A and B occurring can be found using the formula
A rearranged version is given in the formula booklet
Basically you multiply the probability of A by the probability of B then happening
Examiner Tips and Tricks
In an exam drawing a Venn diagram or tree diagram can help even if the question does not ask you to
Worked Example
Dave has two fair spinners, A and B. Spinner A has three sides numbered 1, 4, 9 and spinner B has four sides numbered 2, 3, 5, 7. Dave spins both spinners and forms a two-digit number by using the spinner A for the first digit and spinner B for the second digit.
is the event that the two-digit number is a multiple of 3.
a) List all the possible two-digit numbers.
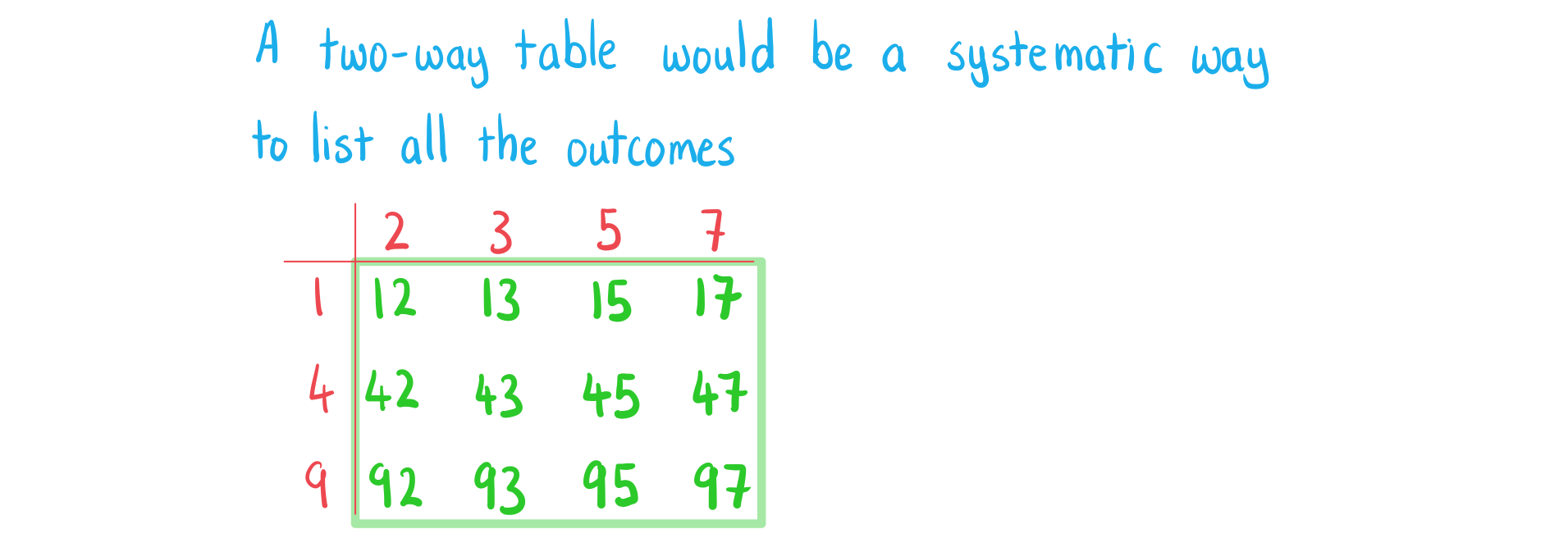
b) Find .
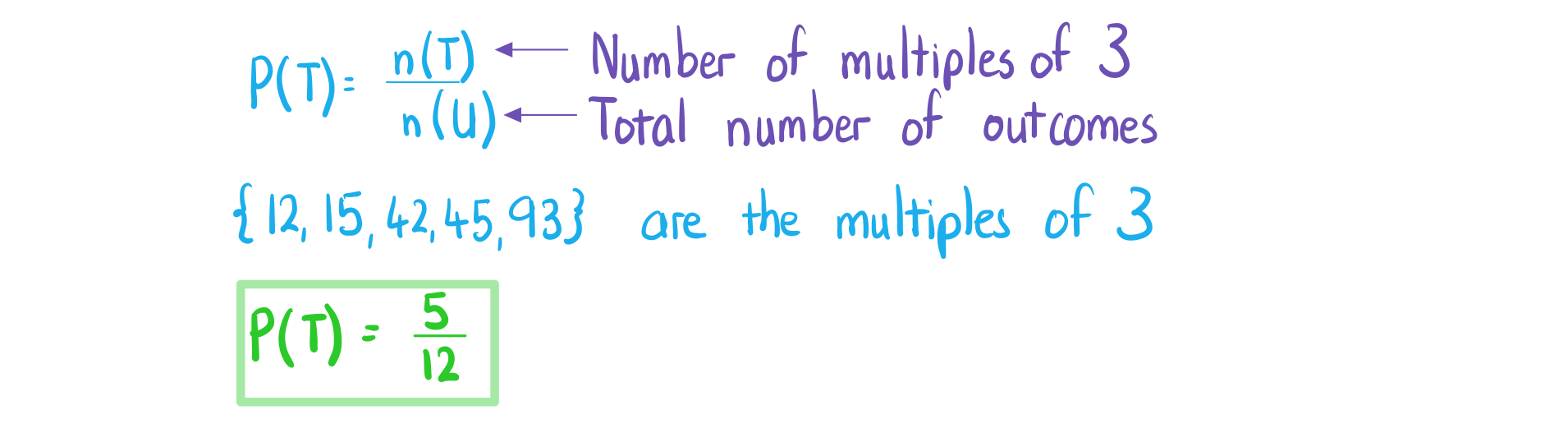
c) Find .
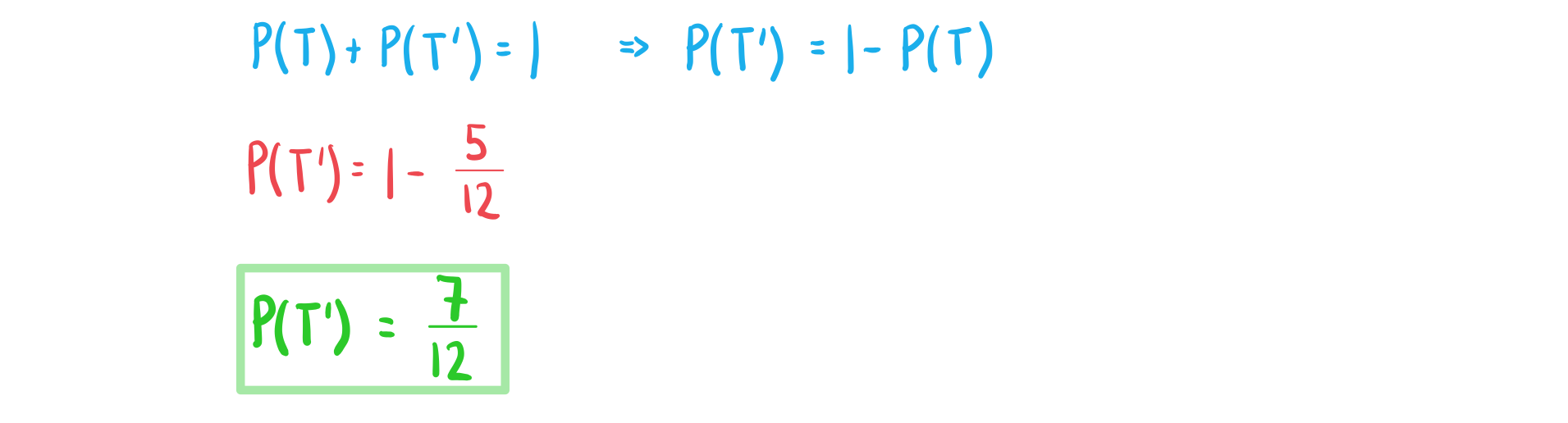

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?