Revision NotesExam QuestionsFlashcardsPast PapersMock Exams
IBMathsDPApplications & Interpretation (AI)HLRevision Notes5. CalculusFurther DifferentiationDifferentiating Special Functions

Differentiating Special Functions (DP IB Applications & Interpretation (AI)): Revision Note

Paul

Author

Paul

Last updated

DP Applications & Interpretation (AI): HLDP Analysis & Approaches (AA): HL

Did this video help you?

Differentiating Trig Functions

How do I differentiate sin, cos and tan?

  • The derivative ofspace bold italic y equals bold sin space bold italic x isspace fraction numerator bold d bold italic y over denominator bold d bold italic x end fraction equals bold cos space bold italic x   

  • The derivative ofbold space bold italic y equals bold cos space bold italic x isspace fraction numerator bold d bold italic y over denominator bold d bold italic x end fraction equals negative bold sin space bold italic x

  • The derivative ofbold space bold italic y bold equals bold tan bold space bold italic x isbold space fraction numerator bold d bold italic y over denominator bold d bold italic x end fraction bold equals fraction numerator bold 1 over denominator bold cos to the power of bold 2 bold space bold italic x end fraction

    • This result can be derived using quotient rule

  • All three of these derivatives are given in the formula booklet

  • For the linear functionbold space bold italic a bold italic x bold plus bold italic b, where bold italic a and bold italic b are constants,

    • the derivative ofbold space bold italic y bold equals bold sin bold left parenthesis bold italic a bold italic x bold plus bold italic b bold right parenthesis isspace fraction numerator bold d bold italic y over denominator bold d bold italic x end fraction bold equals bold italic a bold cos bold left parenthesis bold italic a bold italic x bold plus bold italic b bold right parenthesis 

    • the derivative ofbold space bold italic y bold equals bold cos bold left parenthesis bold italic a bold italic x bold plus bold italic b bold right parenthesis isbold space fraction numerator bold d bold italic y over denominator bold d bold italic x end fraction bold equals bold minus bold italic a bold sin bold left parenthesis bold italic a bold italic x bold plus bold italic b bold right parenthesis

    • the derivative ofbold space bold italic y bold equals bold tan bold left parenthesis bold italic a bold italic x bold plus bold italic b bold right parenthesis isbold space fraction numerator bold d bold italic y over denominator bold d bold italic x end fraction bold equals fraction numerator bold italic a over denominator bold cos to the power of bold 2 bold space bold left parenthesis bold italic a bold italic x bold italic plus bold italic b bold right parenthesis end fraction

  • For the general functionbold space bold italic f bold left parenthesis bold italic x bold right parenthesis,

    • the derivative ofbold space bold italic y equals bold sin stretchy left parenthesis bold italic f left parenthesis bold italic x right parenthesis stretchy right parenthesis isbold space fraction numerator bold d bold italic y over denominator bold d bold italic x end fraction bold equals bold italic f to the power of bold apostrophe bold left parenthesis bold italic x bold right parenthesis bold cos stretchy left parenthesis bold italic f open parentheses x close parentheses stretchy right parenthesis

    • the derivative ofbold space bold italic y equals bold cos stretchy left parenthesis bold italic f left parenthesis bold italic x right parenthesis stretchy right parenthesis isbold space fraction numerator bold d bold italic y over denominator bold d bold italic x end fraction bold equals bold minus bold italic f bold apostrophe bold left parenthesis bold italic x bold right parenthesis bold sin stretchy left parenthesis bold italic f left parenthesis x right parenthesis stretchy right parenthesis

    • the derivative ofbold space bold italic y bold equals bold tan bold left parenthesis bold italic f bold left parenthesis bold italic x bold right parenthesis bold right parenthesis isbold space fraction numerator bold d bold italic y over denominator bold d bold italic x end fraction bold equals fraction numerator bold italic f bold apostrophe bold left parenthesis bold italic x bold right parenthesis over denominator bold cos to the power of bold 2 bold space bold left parenthesis bold italic f bold left parenthesis bold italic x bold right parenthesis bold right parenthesis end fraction

  • These last three results can be derived using the chain rule

  • For calculus with trigonometric functions angles must be measured in radians

    • Ensure you know how to change the angle mode on your GDC

Examiner Tips and Tricks

  • As soon as you see a question involving differentiation and trigonometry put your GDC into radians mode

Worked Example

a) Find space f apostrophe left parenthesis x right parenthesis for the functions

 

  1. space f left parenthesis x right parenthesis equals sin space x

  2. space f left parenthesis x right parenthesis equals cos left parenthesis 5 x plus 1 right parenthesis

5-2-1-ib-hl-ai-aa-extraaa-we1a-soltn

b)       A curve has equationspace y equals tan space stretchy left parenthesis 6 x squared minus straight pi over 4 stretchy right parenthesis space.

Find the gradient of the tangent to the curve at the point where x equals fraction numerator square root of straight pi over denominator 2 end fraction.

Give your answer as an exact value.

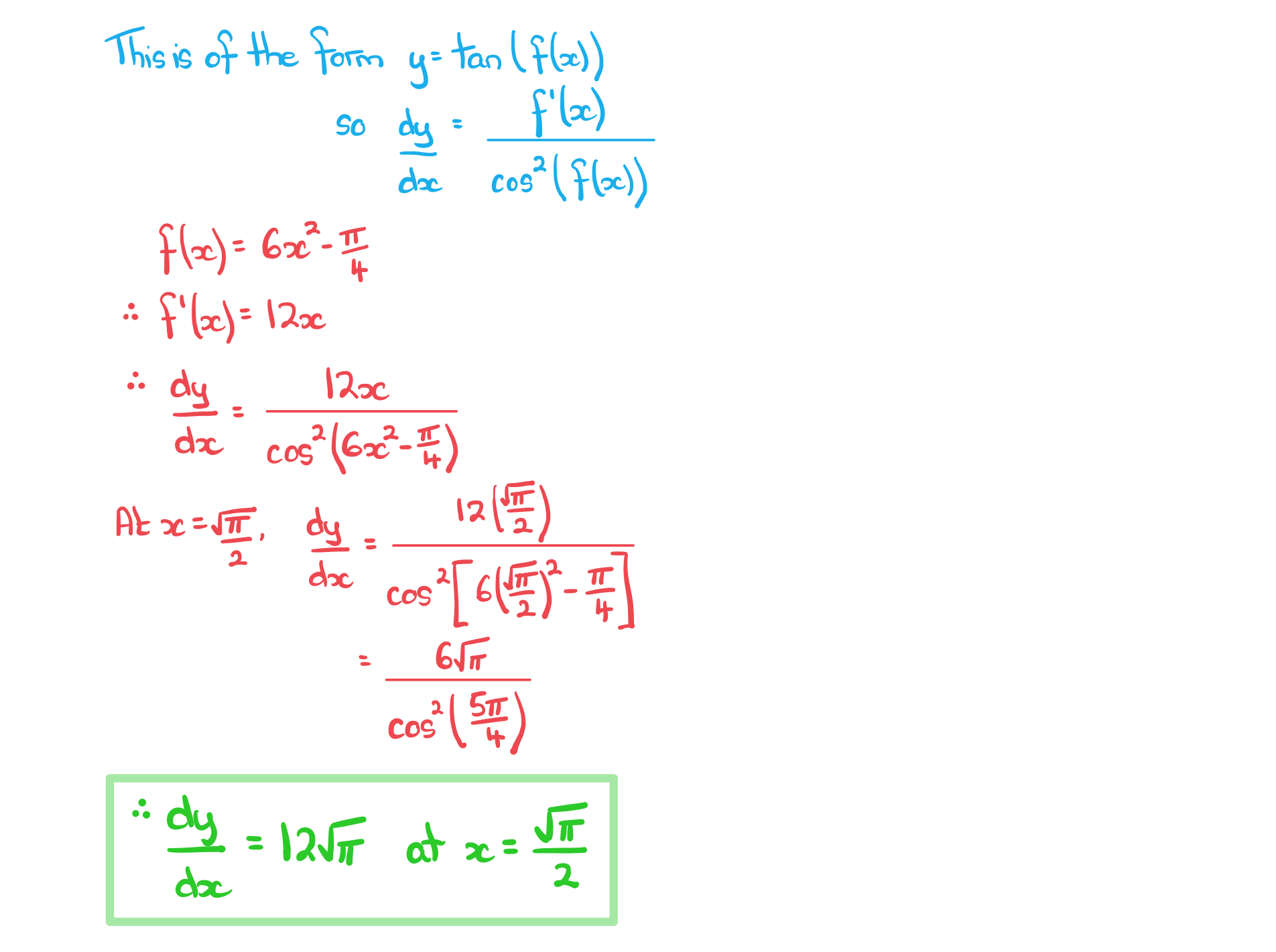
5-2-1-ib-hl-ai-aa-extraaa-ai-we1b-soltn

Did this video help you?

Differentiating e^x & lnx

How do I differentiate exponentials and logarithms?

  • The derivative of bold space bold italic y bold equals bold e to the power of bold italic x is bold space fraction numerator bold d bold italic y over denominator bold d bold italic x end fraction bold equals bold e to the power of bold italic x where x element of straight real numbers

  • The derivative of bold space bold italic y bold equals bold ln bold space bold italic x is bold space fraction numerator bold d bold italic y over denominator bold d bold italic x end fraction bold equals bold 1 over bold italic x where space x greater than 0

  • For the linear function bold space bold italic a bold italic x bold plus bold italic b, where a and b are constants,

    • the derivative of bold space bold italic y bold equals bold e to the power of bold left parenthesis bold italic a bold italic x bold plus bold italic b bold right parenthesis end exponent is text bold end text fraction numerator bold d bold italic y over denominator bold d bold italic x end fraction bold equals bold italic a bold e to the power of bold left parenthesis bold italic a bold italic x bold plus bold italic b bold right parenthesis end exponent

    • the derivative of bold space bold italic y equals bold ln stretchy left parenthesis bold italic a bold italic x plus bold italic b stretchy right parenthesis is Error converting from MathML to accessible text.

      • in the special case space b equals 0, bold space fraction numerator bold d bold italic y over denominator bold d bold italic x end fraction bold equals bold 1 over bold italic x     (a's cancel)

  • For the general function bold space bold f bold left parenthesis bold italic x bold right parenthesis,

    • the derivative of  is 

    • the derivative of  is 

  • The last two sets of results can be derived using the chain rule

Examiner Tips and Tricks

  • Remember to avoid the common mistakes:

    • the derivative ofspace ln space k x with respect to x isspace 1 over x, NOTspace k over x

    • the derivative of straight e to the power of k x end exponent with respect to x is k straight e to the power of k x end exponent, NOT k x straight e to the power of k x minus 1 end exponent

Worked Example

A curve has the equationsize 16px space size 16px y size 16px equals size 16px e to the power of size 16px minus size 16px 3 size 16px x size 16px plus size 16px 1 end exponent size 16px plus size 16px 2 size 16px ln size 16px space size 16px 5 size 16px x.

Find the gradient of the curve at the point wherespace x equals 2 gving your answer in the form y equals a plus b e to the power of c, where a comma space b and c are integers to be found.

5-2-1-ib-sl-aa-only-we2-soltn

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:Modelling with DifferentiationNext:Techniques of Differentiation
    Paul

    Author: Paul

    Expertise: Maths Content Creator

    Paul has taught mathematics for 20 years and has been an examiner for Edexcel for over a decade. GCSE, A level, pure, mechanics, statistics, discrete – if it’s in a Maths exam, Paul will know about it. Paul is a passionate fan of clear and colourful notes with fascinating diagrams.