IGCSEFurther MathsCambridge (CIE)Additional MathsRevision NotesAlgebra & FunctionsFunctionsInverse Functions

Inverse Functions (Cambridge (CIE) IGCSE Additional Maths) : Revision Note

Paul

Author

Paul

Last updated

Inverse Functions

What is an inverse function?

  • An inverse function does the exact opposite of the function it came from

    • For example, if the function “doubles the number and adds 1” then its inverse is

    • “subtract 1 and halve the result”

  • It is the inverse operations in the reverse order

How do I write inverse functions?

  • An inverse function f-1 can be written as space straight f to the power of negative 1 end exponent left parenthesis x right parenthesis space equals space horizontal ellipsis space space or  straight f to the power of negative 1 end exponent space colon space x space rightwards arrow from bar space horizontal ellipsis

    • For example, if straight f left parenthesis x right parenthesis space equals space 2 x space plus space 1 its inverse can be written as

    • straight f to the power of negative 1 end exponent left parenthesis x right parenthesis space equals space fraction numerator left parenthesis x space – space 1 right parenthesis space over denominator 2 end fraction  or   straight f to the power of negative 1 end exponent colon space x space rightwards arrow from bar space fraction numerator left parenthesis x space – space 1 right parenthesis over denominator 2 end fraction

How do I find an inverse function?

  • The easiest way to find an inverse function is to 'cheat' and swap the x and y variables

    • Note that this is a useful method but you MUST remember not to do this in any other circumstances in maths

  • STEP 1 Write the function in the formspace y space equals space horizontal ellipsis e.g.   y space equals space 2 x space plus space 1

  • STEP 2 Swap the x's andspace y's to get x space equals space horizontal ellipsis e.g.  x space equals space 2 y space plus space 1

  • STEP 3 Rearrange the expression to make y the subject again table row cell x space minus space 1 space end cell equals cell space 2 y end cell row cell fraction numerator x space minus space 1 over denominator 2 end fraction space end cell equals cell space y space space space space space space rightwards arrow space space space y space equals space fraction numerator x space minus space 1 over denominator 2 end fraction end cell end table

  • STEP 4 Rewrite using the correct notation for an inverse function

    • either as f-1(x) = … or f-1 : x ↦ …

    • yshould not exist in the final answer

      • e.g.  straight f to the power of negative 1 end exponent open parentheses x close parentheses space equals space fraction numerator space x italic space minus space 1 over denominator 2 end fraction

How does a function relate to its inverse?

  • If straight f open parentheses 3 close parentheses equals 10 then the input of 3 gives an output of 10

    • The inverse function undoes f(x)

    • An input of 10 into the inverse function gives an output of 3

      • If straight f open parentheses 3 close parentheses equals 10 then straight f to the power of negative 1 end exponent open parentheses 10 close parentheses equals 3

  • ff to the power of negative 1 end exponent open parentheses x close parentheses equals straight f to the power of negative 1 end exponent straight f open parentheses x close parentheses equals x

    • If you apply a function to x, then immediately apply its inverse function, you get x

      • Whatever happened to x gets undone

    • f and f-1 cancel each other out when applied together

  • If straight f open parentheses x close parentheses space equals space 2 to the power of x and you want to solve straight f to the power of negative 1 end exponent open parentheses x close parentheses space equals space 5

    • Finding the inverse function straight f to the power of negative 1 end exponent open parentheses x close parentheses in this case is tricky (impossible if you haven't studied logarithms)

    • instead, take f of both sides and use that ff to the power of negative 1 end exponent cancel each other out:

table row cell ff to the power of negative 1 end exponent open parentheses x close parentheses end cell equals cell straight f open parentheses 5 close parentheses end cell row x equals cell straight f open parentheses 5 close parentheses end cell row x equals cell 2 to the power of 5 equals 32 end cell end table

Worked Example

Find the inverse of the function straight f open parentheses x close parentheses space equals space 5 space minus space 3 x.

Write the function in the form y space equals space 5 space minus space 3 x and then swap the x and y.  

y space equals space 5 space minus space 3 x x space equals space 5 space minus space 3 y

Rearrange the expression to make y the subject again.

table row cell x space end cell equals cell space 5 space minus space 3 y end cell row cell space x space plus space 3 y space end cell equals cell space 5 end cell row cell 3 y space end cell equals cell space 5 space minus space x end cell row cell y space end cell equals cell space fraction numerator 5 space minus space x over denominator 3 end fraction end cell end table

  Rewrite using the correct notation for an inverse function.

Domain & Range of Inverse Functions

How do I find the domain and range of inverse functions?

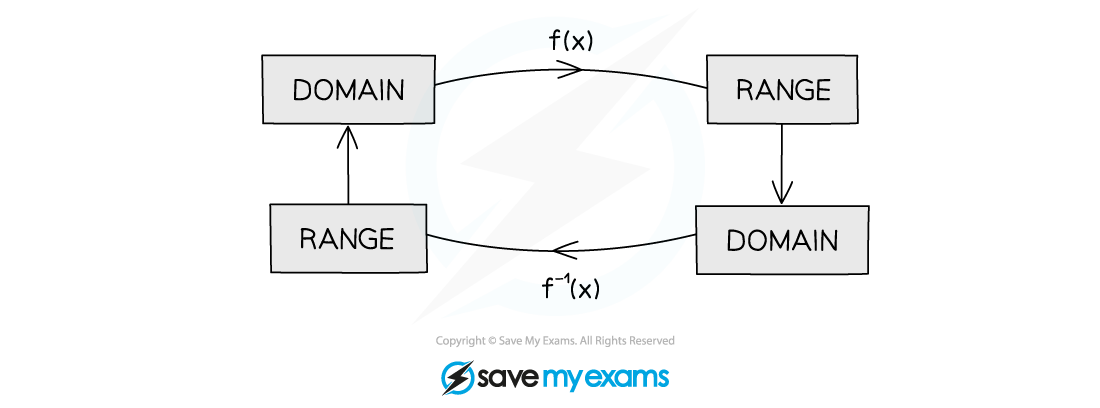
Domain and range of a function swap for its inverse

 

  • The range of a function will be the domain of its inverse function

  • The domain of a function will be the range of its inverse function

Worked Example

A function is defined as straight f stretchy left parenthesis x stretchy right parenthesis equals square root of 3 x minus 2 end root comma space space x greater than fraction numerator 3 over denominator 2 space end fraction.

Write down the domain and range of straight f to the power of negative 1 end exponent stretchy left parenthesis x stretchy right parenthesis.

The domain of an inverse function is the range of the function.

The range of straight f open parentheses x close parentheses is

straight f greater than 0

therefore The domain of  is bold italic x bold greater than bold 0

The range of an inverse function is the domain of the function.

therefore The range of is bold f to the power of bold minus bold 1 end exponent bold greater than bold 3 over bold 2

Graphs of Inverse Functions

  • The graph of an inverse function, y equals straight f to the power of negative 1 end exponent open parentheses x close parentheses, is a reflection of the graph of the function, y equals straight f open parentheses x close parentheses, in the line y equals x

  • Key features of the graph of y equals straight f open parentheses x close parentheses will be reflected, such as

    • x and y axes intercepts

    • turning points

    • asymptotes

How do I sketch the graph of an inverse function?

  • STEP 1

    • Sketch the line y equals x, and if need be, the graph of y equals straight f open parentheses x close parentheses

  • STEP 2

    • Reflect the graph of y equals straight f open parentheses x close parentheses in the line y equals x

      • Remember it is a sketch, but the graphs together should look like reflections

    • Consider points where the reflected graph will intersect the x and y axes

      • e.g.  The point open parentheses 4 comma space 0 close parentheses will be reflected to the point open parentheses 0 comma space 4 close parentheses

    • Consider any asymptotes on the graph of y equals straight f open parentheses x close parentheses - these will also be need reflecting

      • e.g.  The asymptote (line) x equals negative 2 will be reflected to the line y equals negative 2

    • Consider any restrictions on the domain and range of straight f open parentheses x close parentheses

      • e.g.  If the domain is x greater than 0 only sketch the graph for positive values of x

  • STEP 3

    • Label key points on the sketch of y equals straight f to the power of negative 1 end exponent open parentheses x close parentheses and state the equations of any asymptotes

  • This process works the other way round - the graph of y equals straight f open parentheses x close parentheses can be sketched from the graph of y equals straight f to the power of negative 1 end exponent open parentheses x close parentheses

Examiner Tips and Tricks

  • If not given, sketch the graphs of y equals straight f open parentheses x close parentheses and y equals x to help sketch the graph of the inverse, y equals straight f to the power of negative 1 end exponent open parentheses x close parentheses

  • If the graph of y equals straight f open parentheses x close parentheses is given you do not need to know the expression for straight f open parentheses x close parentheses to sketch y equals straight f to the power of negative 1 end exponent open parentheses x close parentheses

    • Just reflect whatever is given in the line y equals x

Worked Example

The diagram below shows the graph of y equals straight f open parentheses x close parentheses, where straight f open parentheses x close parentheses equals 4 minus 4 over x comma space space x greater than 0.

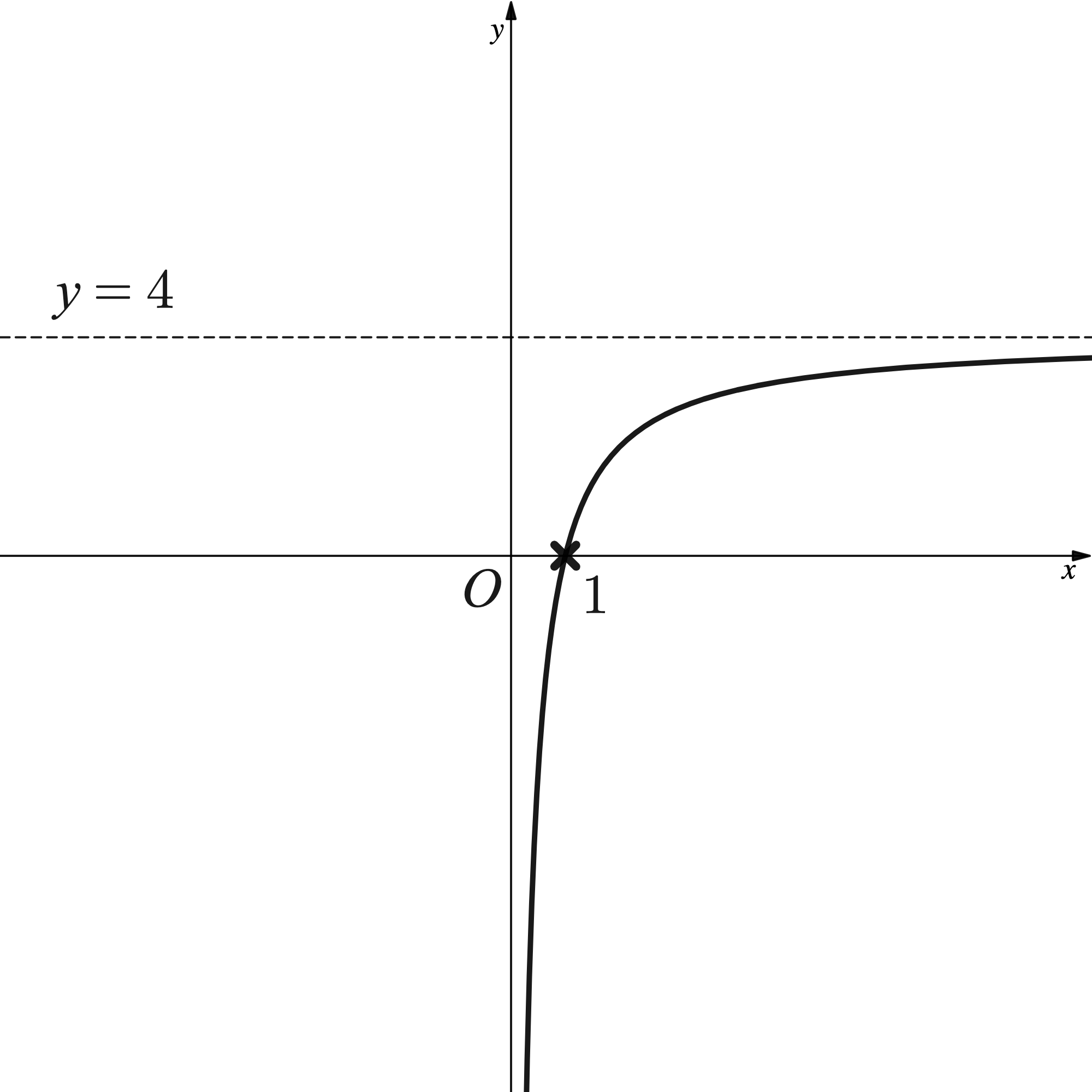
desmos-graph-6

a)On a copy of the diagram, sketch the graph of y equals straight f to the power of negative 1 end exponent open parentheses x close parentheses. Label the point where the graph crosses the y-axis and write down the equation of the asymptote.

The graph of an inverse function is the reflection of the graph of that function in the line y equals x.

Draw the line y equals x to help sketch the inverse function.

The x-axis intercept open parentheses 1 comma space 0 close parentheses becomes the y-axis intercept, open parentheses 0 comma space 1 close parentheses.

The (horizontal) asymptote y equals 4 will. become the (vertical) asymptote x equals 4.

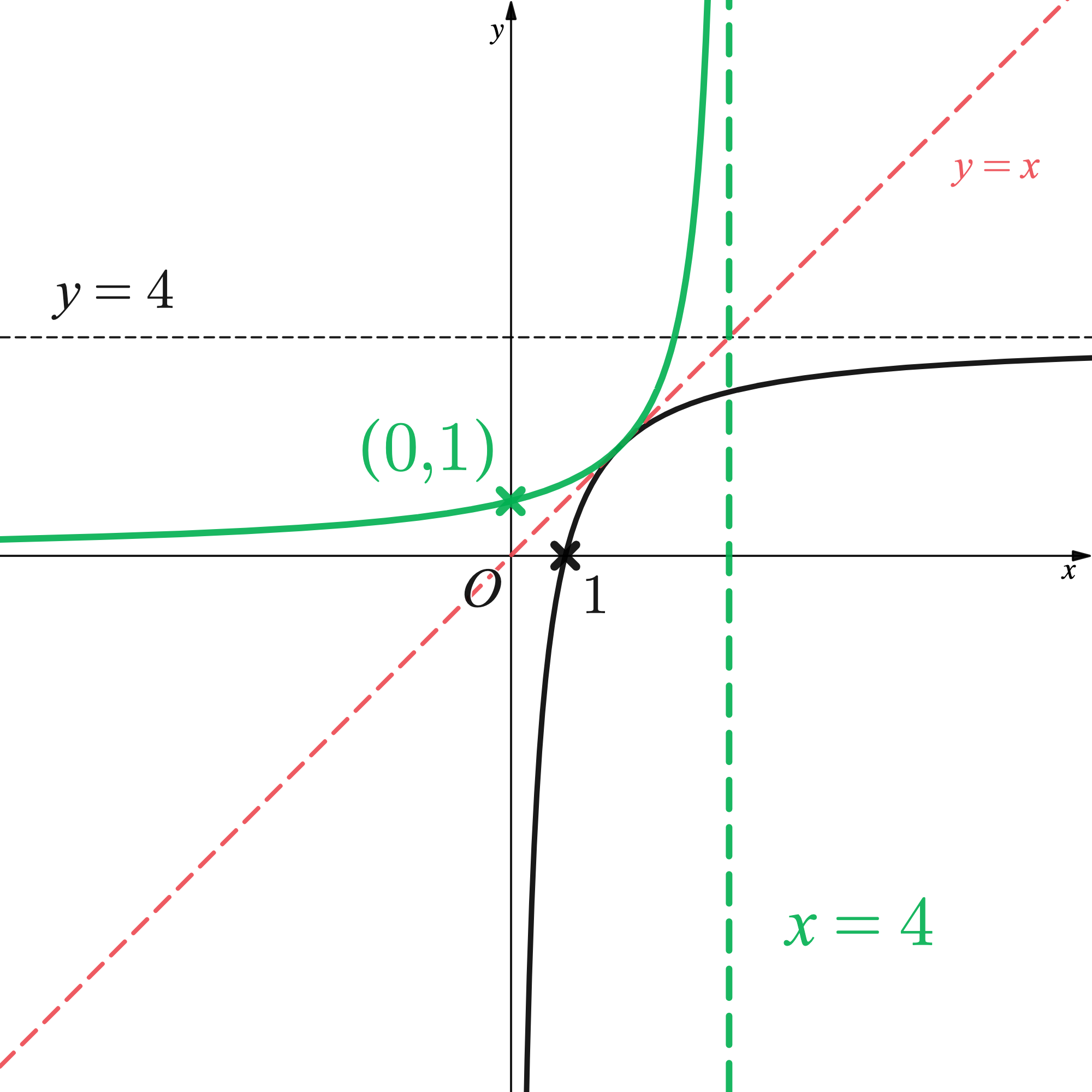
desmos-graph-5

b) Use your sketch, or otherwise, to write down the value of x such that straight f open parentheses x close parentheses equals straight f to the power of negative 1 space end exponent open parentheses x close parentheses.

This will be the point at which the two graphs meet.

The point will be on the line y equals x so there is no need to work out straight f to the power of negative 1 end exponent open parentheses x close parentheses.

By sketching the graph in part (a) this point (with coordinates open parentheses 2 comma space 2 close parentheses) should have already been considered. Only the x value is required.

bold italic x bold equals bold 2

The x value could also be found by solving straight f open parentheses x close parentheses equals x.

👀 You've read 1 of your 5 free revision notes this week
An illustration of students holding their exam resultsUnlock more revision notes. It's free!

By signing up you agree to our Terms and Privacy Policy.

Already have an account? Log in

Test yourself

Did this page help you?

Previous:Language of FunctionsNext:Composite Functions
Paul

Author: Paul

Expertise: Maths Content Creator (Previous)

Paul has taught mathematics for 20 years and has been an examiner for Edexcel for over a decade. GCSE, A level, pure, mechanics, statistics, discrete – if it’s in a Maths exam, Paul will know about it. Paul is a passionate fan of clear and colourful notes with fascinating diagrams.

Download notes on Inverse Functions