Study GuidesExam QuestionsPast PapersMock Exams
AP®PhysicsCollege BoardPhysics 1: Algebra-BasedExam QuestionsUnit 6: Energy & Momentum of Rotating SystemsConservation of Angular Momentum

Conservation of Angular Momentum (College Board AP® Physics 1: Algebra-Based): Exam Questions

27 mins17 questions

Select a download format for Conservation of Angular Momentum

Scroll for more

Select an answer set to view for
Conservation of Angular Momentum

1a
Sme Calculator2 marks
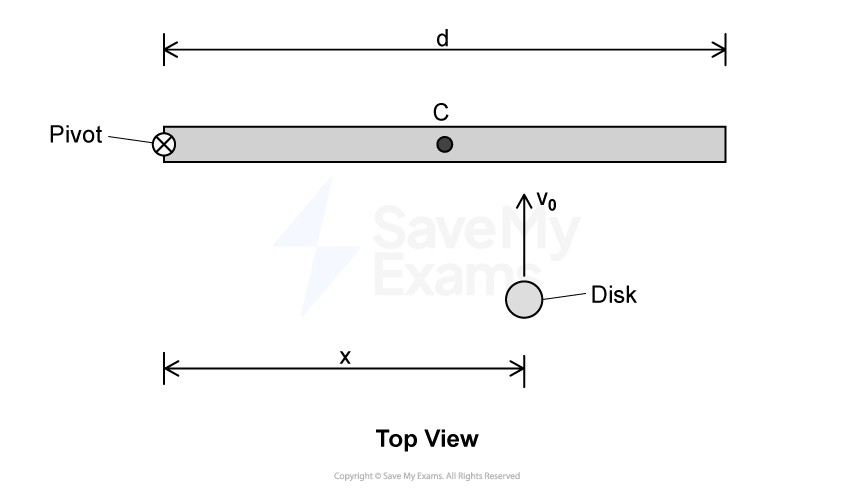
Top view diagram of a rod of length d pivoted at its left end with a disk moving towards it with speed v0. The midpoint of the rod is marked C and the distance from the disk to the pivot is x.

Figure 1

The left end of a rod of length d and rotational inertia I is attached to a frictionless horizontal surface by a frictionless pivot, as shown in Figure 1. Point C marks the center (midpoint) of the rod. The rod is initially at rest but is free to rotate around the pivot. A disk of mass m subscript d i s k end subscript slides towards the rod with velocity v subscript 0 perpendicular to the rod. Following the collision, the disk sticks to the rod a distance x from the pivot.

If the disk is much less massive than the rod, indicate whether the rod would gain the largest angular speed if the disk were to hit the rod to the left of point C, at point C, or to the right of point C.

⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽ To the left of C‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽ At C ‎ ‎ ‎‎ ‎ ‎ ‎ ‎ ‎ ‎ ⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽ To the right of C

Justify your answer using qualitative reasoning beyond referencing equations.

How did you do?

1b
Sme Calculator3 marks

Starting with conservation of angular momentum, derive an equation for omega, the angular speed of the rod after the collision, in terms of d, m subscript d i s k end subscript, I, x, and v subscript 0. Begin your derivation by writing a fundamental physics principle or an equation from the reference book.

How did you do?

1c
Sme Calculator3 marks

The experiment is repeated with a second disk. Following the collision, the second disk bounces backward instead of sticking to the rod. The angular speed of the rod after the second collision is omega apostrophe.

Indicate whether omega apostrophe is greater than, less than, or equal to omega.

⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽ omega apostrophe space greater than space omega‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽ omega apostrophe space equals space omega ‎ ‎ ‎‎ ‎ ‎ ‎ ‎ ‎ ‎ ⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽ omega apostrophe space less than space omega

Justify your reasoning using the equation you derived in part b).

How did you do?

Did this page help you?

2
Sme Calculator4 marks
A ball on the ground just below a pivot connected to a horizontal rod, with a curved dashed line representing the rotational path of the end of the rod once released.

Figure 1

A system consists of a small sphere of mass m and radius R at rest on a horizontal surface and a uniform rod of mass M space equals space 2 m and length l attached at one end to a pivot with negligible friction, where R space much less-than space l. There is negligible friction between the surface and the sphere. The rod is held horizontally as shown in Figure 1, and then is released from rest. The total rotational inertia of the rod about the pivot is 1 third M l squared. After the rod is released, the rod swings down and strikes the sphere head-on. As a result of this collision, the rod is stopped, and the ball initially slides without rolling to the left across the horizontal surface.

i) Starting with conservation of energy, derive an expression for the angular speed of the rod just before striking the sphere in terms of l and physical constants as appropriate. Begin your derivation by writing a fundamental physics principle or an equation from the reference information.

ii) Starting with conservation of angular momentum, derive an expression for the linear speed v subscript 0 of the sphere immediately after colliding with the rod in terms of l and physical constants as appropriate. Begin your derivation by writing a fundamental physics principle or an equation from the reference information.

How did you do?

Did this page help you?