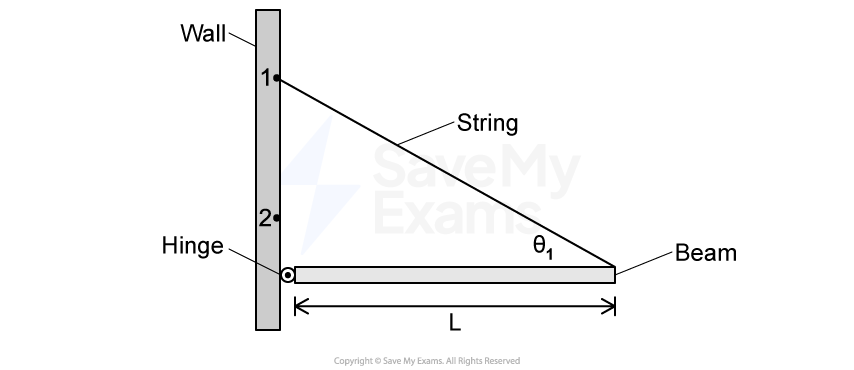
Figure 1
A physics class is asked to design a low-friction slide that will launch a block horizontally from the top of a lab table. Teams 1 and 2 assemble the slides as shown in Figure 1 and use identical blocks 1 and 2, respectively. Both slides start at the same height above the table top. However, Team 2's table is lower than Team 1's table. To compensate for the lower table, Team 2 constructs the right end of the slide to rise above the table top so that the block leaves the slide horizontally at the same height
above the floor as does Team 1's block.
Both blocks are released from rest at the top of their respective slides. Block 1 lands a horizontal distance , and Block 2 lands a horizontal distance
from their respective tables.
Indicate whether is greater than, less than, or equal to
.
⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽ ⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽
⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽
Justify your answer using qualitative reasoning beyond referencing equations.
Derive an expression for the time taken by Block 1 to hit the floor after leaving the slide in terms of ,
,
and physical constants as appropriate. Begin your derivation by writing a fundamental physics principle or an equation from the reference book.
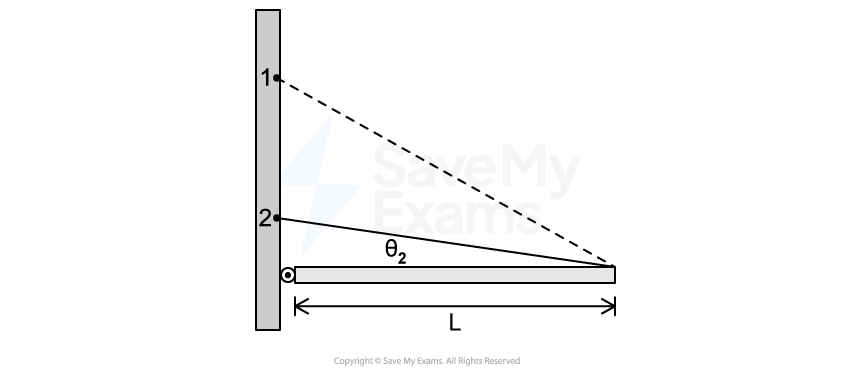
In another experiment, teams 1 and 2 use tables and low friction slides with the same height. However, the two slides have different shapes, as shown in Figure 2.

Figure 2
Both blocks 1 and 2 are released from rest at the top of their respective slides at the same time.
Predict how the time of flight of blocks 1 and 2 would differ. Use the equation derived in part b) to justify your answer.
Did this page help you?