Revision NotesExam QuestionsFlashcardsPast PapersMock Exams
IBMathsDPApplications & Interpretation (AI)HLRevision Notes2. FunctionsFurther Functions & GraphsExponential Functions & Graphs

Exponential Functions & Graphs (DP IB Applications & Interpretation (AI)): Revision Note

Dan Finlay

Written by: Dan Finlay

Reviewed by: Lucy Kirkham

Updated on

DP Applications & Interpretation (AI): HLDP Applications & Interpretation (AI): SLDP Applications & Interpretation (AI): HLDP Applications & Interpretation (AI): SL

Exponential functions & graphs

What are the key features of exponential graphs?

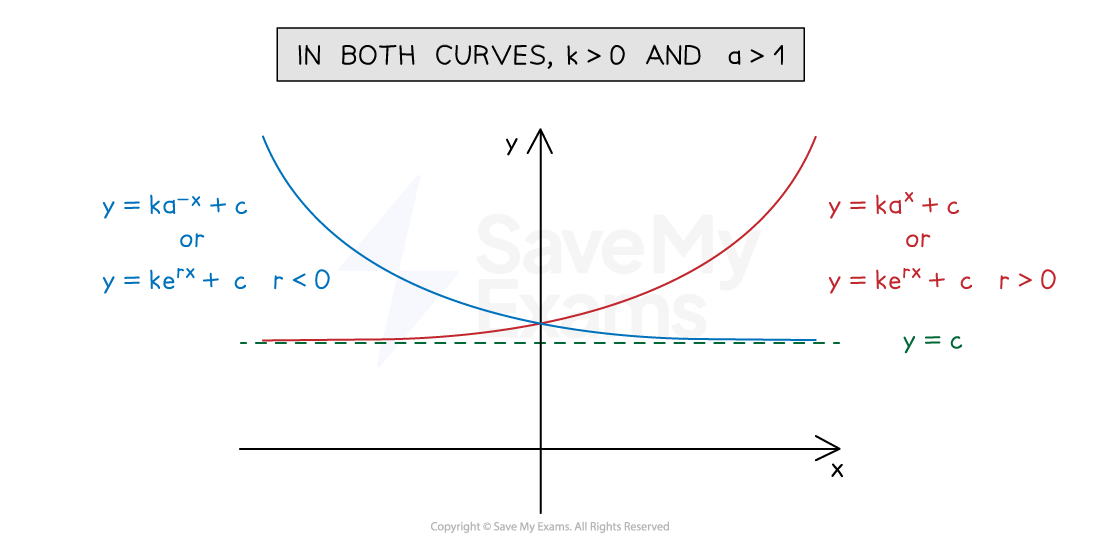
  • An exponential graph is of the form

    • space y equals k a to the power of x plus c or space y equals k a to the power of negative x end exponent plus c where space a greater than 0

    • space y equals k straight e to the power of r x end exponent plus c

      • Where e is the mathematical constant 2.718…

  • The y-intercept is at the point left parenthesis 0 comma space k space plus space c right parenthesis

    • You can find this by substituting x equals 0 into the equation

  • There is a horizontal asymptote at y space equals space c

  • The value of k determines whether the graph is above or below the asymptote

    • If k is positive the graph is above the asymptote

      • So the range is space y greater than c

    • If k is negative the graph is below the asymptote

      • So the range is space y less than c

  • The coefficient of x and the constant k determine whether the graph is increasing or decreasing

    • If the coefficients of x and k have the same sign then graph is increasing

      • e.g. y equals 3 open parentheses 2 close parentheses to the power of x plus 1 and y equals negative 3 straight e to the power of negative 1.5 x end exponent plus 4 are increasing

    • If the coefficients of x and k have different signs then the graph is decreasing

      • e.g. y equals 3 open parentheses 2 close parentheses to the power of negative x end exponent plus 1 and y equals negative 3 straight e to the power of 1.5 x end exponent minus 4 are decreasing

  • There is at most 1 root

    • It can be found using your GDC

Graph showing exponential decay (blue curve) and growth (red curve) with equations. Horizontal line at y = c. Conditions: k > 0, a > 1. Axes labelled x and y.
Examples of exponential graphs and their key features

Examiner Tips and Tricks

You may have to change the viewing window settings on your GDC to make asymptotes clear. A small scale can make it look as though the curve and an asymptote intercept.

Be careful about how two exponential graphs drawn on the same axes look, particularly which one is "on top" either side of the y-axis.

Worked Example

a) On the same set of axes sketch the graphs space y equals 2 to the power of x and space y equals 3 to the power of x. Clearly label each graph.

2-2-3-ib-ai-sl-exp-graphs-a-we-solution

b) Sketch the graph space y equals 2 straight e to the power of negative 3 x end exponent plus 1.

2-2-3-ib-ai-sl-exp-graphs-b-we-solution

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself
    Previous:Cubic Functions & GraphsNext:Sinusoidal Functions & Graphs
    Author
    Reviewer
    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

    Lucy Kirkham

    Reviewer: Lucy Kirkham

    Expertise: Head of Content Creation

    Lucy has been a passionate Maths teacher for over 12 years, teaching maths across the UK and abroad helping to engage, interest and develop confidence in the subject at all levels.Working as a Head of Department and then Director of Maths, Lucy has advised schools and academy trusts in both Scotland and the East Midlands, where her role was to support and coach teachers to improve Maths teaching for all.