Drawing Voronoi Diagrams (DP IB Applications & Interpretation (AI)): Revision Note
Did this video help you?
Drawing Voronoi diagrams
What are Voronoi Diagrams?
Voronoi diagrams are used when you have a fixed number of points and want to find the regions which are closest to specific points
e.g. you might have five parks in a city and want to find the five areas which are closest to each park
A Voronoi diagram splits the area into regions based on sites
A site is located at the coordinates of a specific place of interest
The regions are often called Voronoi cells
Each site has one associated region
e.g, if there are 5 sites then there are 5 regions
The region is the set of all points which are closer to that site than to any other site on the diagram
An edge between two regions is a segment of the perpendicular bisector between the two associated sites
The edges are also called boundaries
The vertices of each region are the intersections of three of these perpendicular bisectors
The vertex is equidistant from the three sites
How do I draw a Voronoi diagram for three sites?
STEP 1
Draw the perpendicular bisector between two of the sites (A and B)Use a dashed line
Label it
STEP 2
Draw the perpendicular bisector between any pair of sites (A and C)Use a dashed line
Label it
STEP 3
Draw the perpendicular bisector between the final pair of sites (B and C)Use a dashed line
Label it
STEP 4
Find the correct boundaries using the intersection of all three linesFor site A:
Draw over the lines
and
Stop at the intersection
The lines should enclose point A
Repeat for sites B and C:
Use
and
for B
Use
and
for C
STEP 5
Erase the remaining parts of the dashed lines
Examiner Tips and Tricks
You will not be expected to draw a Voronoi diagram from scratch, however you should understand how one is constructed.
How do I add a site to a Voronoi diagram?
STEP 1
Draw the perpendicular bisector between the new site and the site in the same cellStop when the line intersects with a current boundary
STEP 2
Draw the perpendicular bisectors between the new site and the site in each of the neighbouring cellsOnly draw parts of the lines which will enclose the new site
These will either stop when they intersect a current boundary
Or join two intersections together
STEP 3
Erase lines and shorten lines to create the cell for the new siteThe new cell should be made up of the new lines
How do I find the equation of an edge?
Each edge is a perpendicular bisector between two sites
To find the equation you first need to find
The midpoint of the two sites
The gradient of the line segment between the two sites
The gradient of the perpendicular line
You can then use the equation of a straight line
How do I find the location of a missing site?
Select an edge around the cell of the missing site
Try to pick an easy edge such as one that is horizontal or vertical
Find the perpendicular distance between a site in a neighbouring cell and the edge
Repeat this distance on the other side of the edge
This is the location of the missing site
Examiner Tips and Tricks
Keep your lines light and dashed until you are confident of your answer.
Worked Example
The Voronoi diagram below shows sites A, B, C and D.
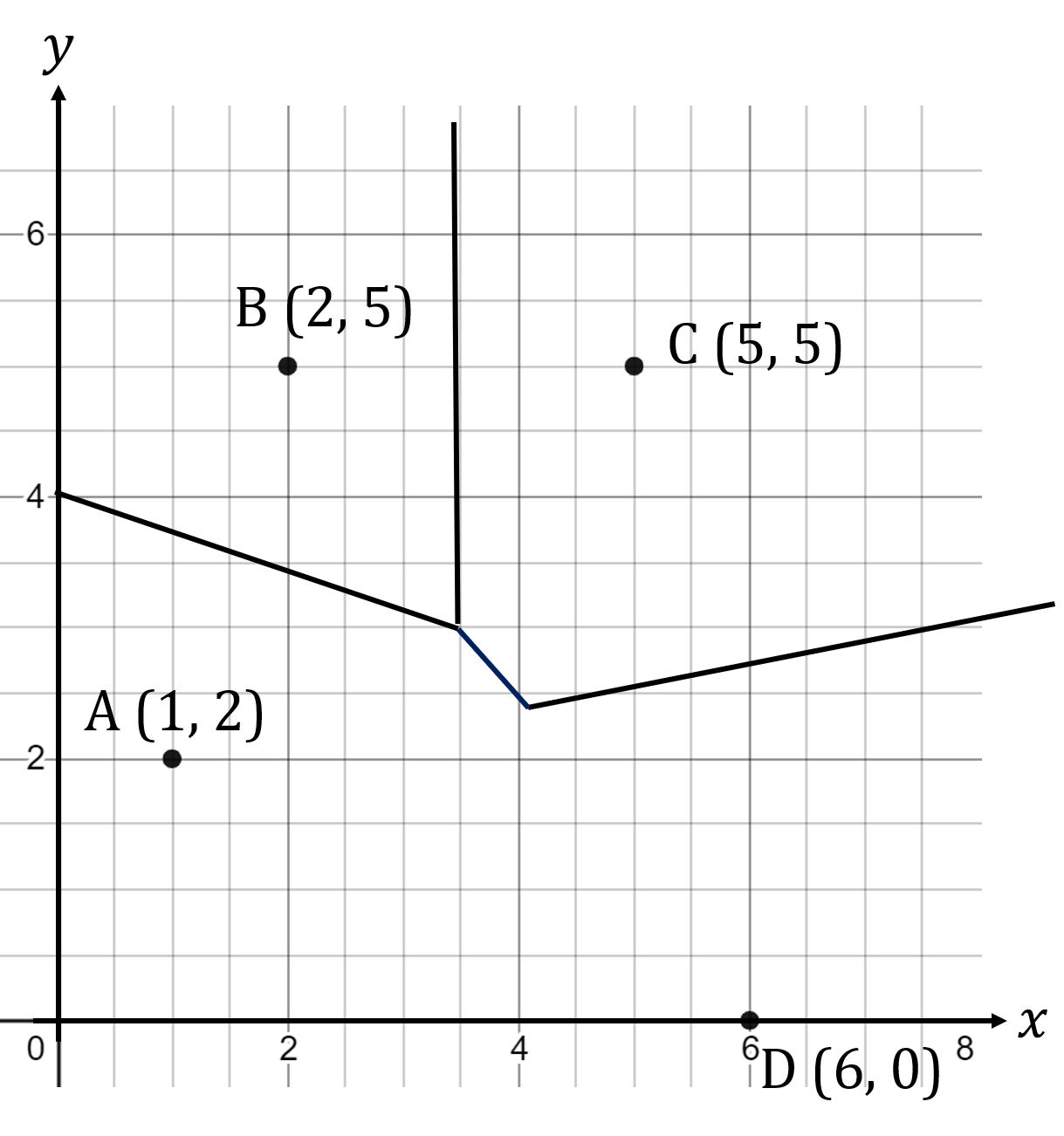
a) Explain how you know that the Voronoi diagram is incomplete.

b) Find the equation of the line which would complete the Voronoi cell containing site A.
Give your answer in the form where
.


Unlock more, it's free!
Did this page help you?