Sigma Notation (DP IB Applications & Interpretation (AI)): Revision Note
Did this video help you?
Sigma notation
What is sigma notation?
Sigma notation shows the sum of a certain number of terms in a sequence
The symbol Σ is the capital Greek letter 'sigma' and stands for 'sum'
e.g. for
The formula after the Σ tells you how to work out each term
It is the nth term formula but written in
instead
The lower limit tells you which term to start on
The upper limit tells you which term to end on
So

The letter
can also be used (instead of
)
Be careful, as not all lower limits start at 1
For example
or
Examiner Tips and Tricks
Your GDC can use sigma notation, which gives you a good way to check your answers to questions involving summing terms!
Worked Example
A sequence is defined by for
.
(a) Write an expression for using sigma notation.
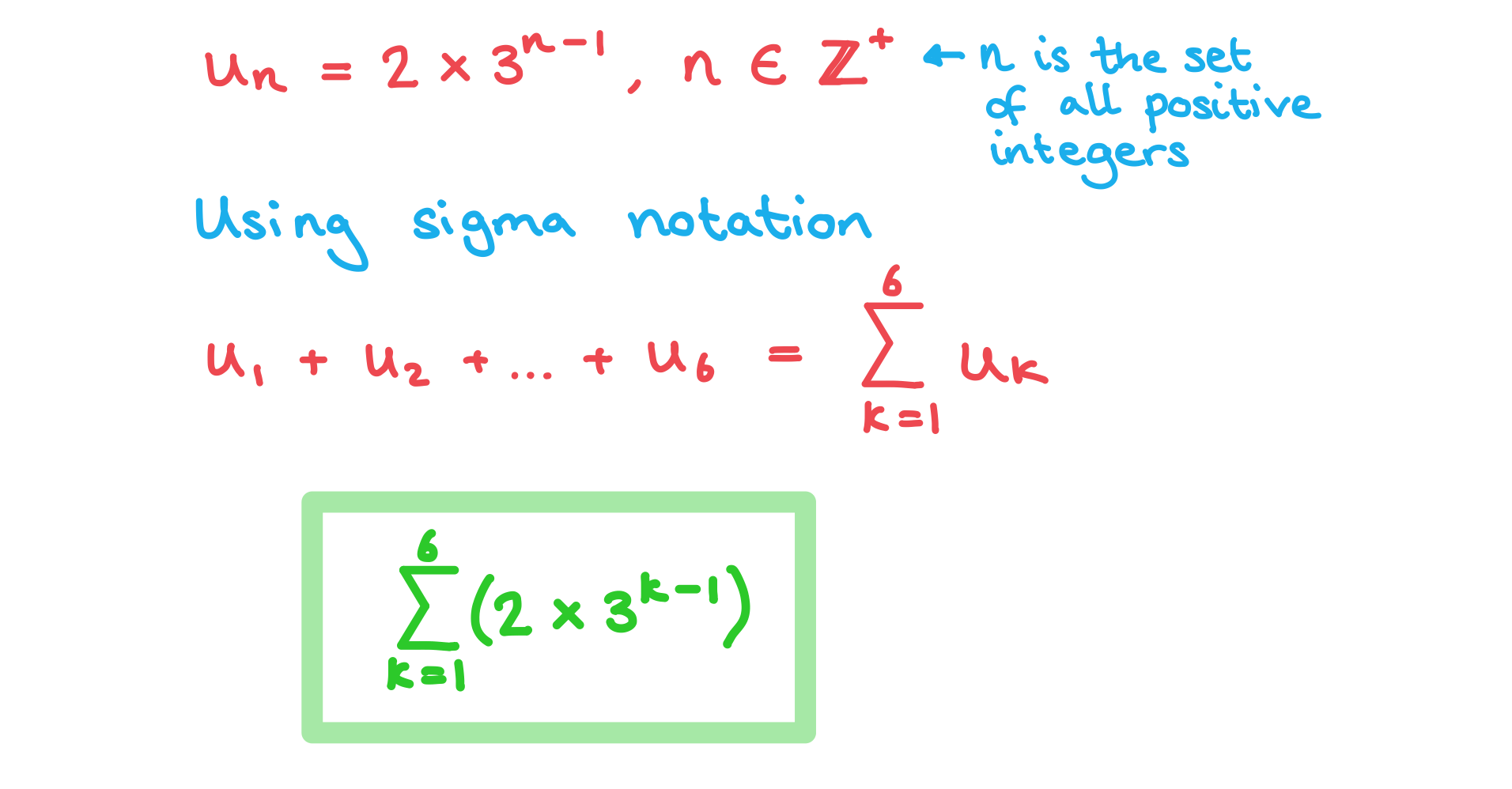
(b) Write an expression for using sigma notation.
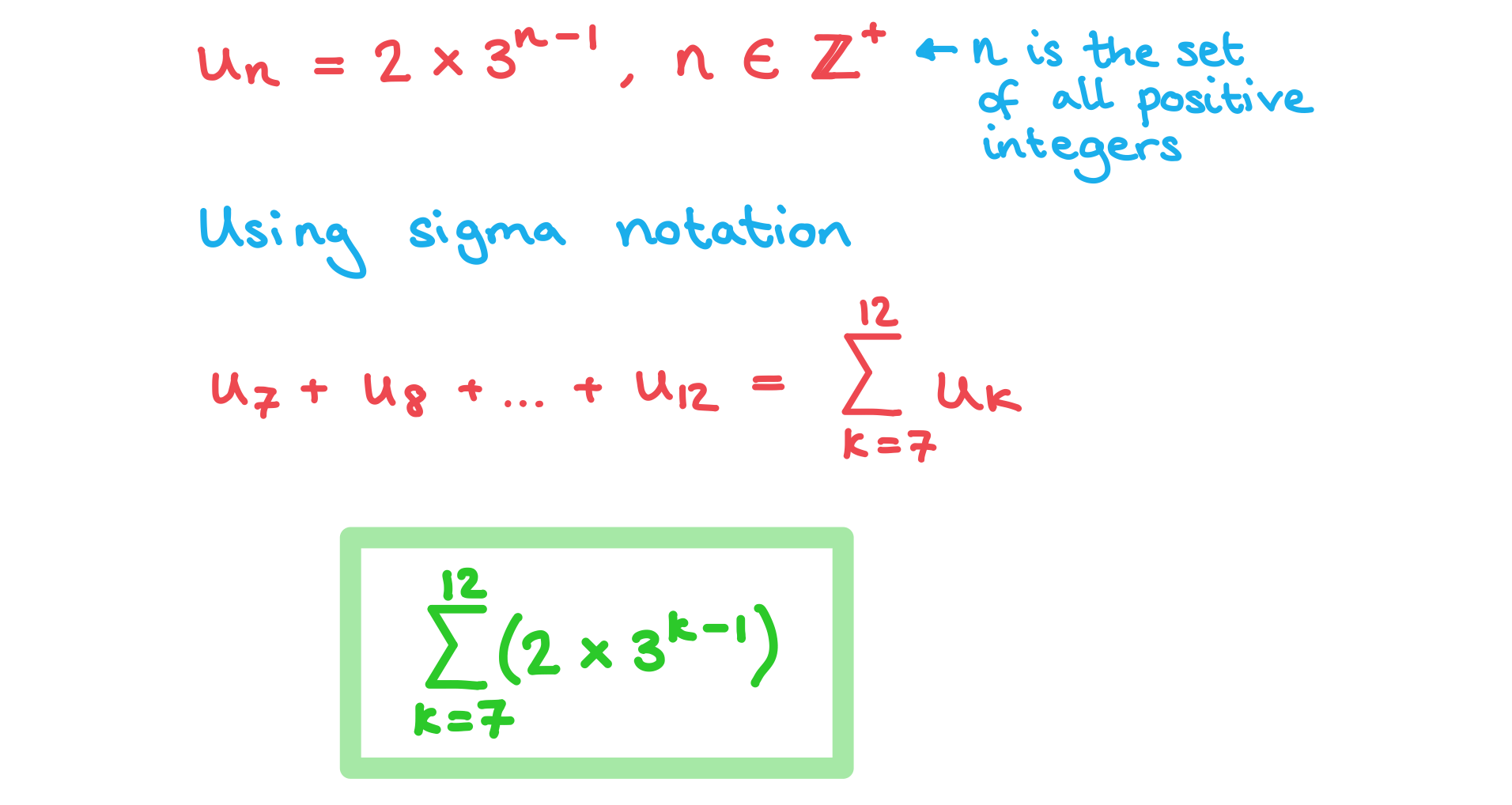

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?