Multiplication & Division (OCR GCSE Maths) : Revision Note

Multiplication

How do I multiply two numbers without a calculator?

• There are a variety of written methods that can be used to add large numbers

  • You only need to know one method, but be able to use it confidently

  • Four common methods are described below, but there are many other valid methods

How do I use the column method?

• This is an efficient method if you are confident with multiplication

• To use the column method:

  • Write one number above the other lining up the digits using place value columns

  • Multiply the first digit (on the right) from the bottom value by each digit in the top value

    • Write the result under the line with the digits in the correct place value columns

  •  Multiply the next digit in the bottom value by each digit in the top value 

    • Always work from right to left

    • Use 0s as place holders when multiplying digits in columns other than the ones column

  • For example, 87 × 426 = 37 062

    

How do I use the lattice method?

• The lattice method is good for numbers with two or more digits

  • This method allows you to work with individual digits

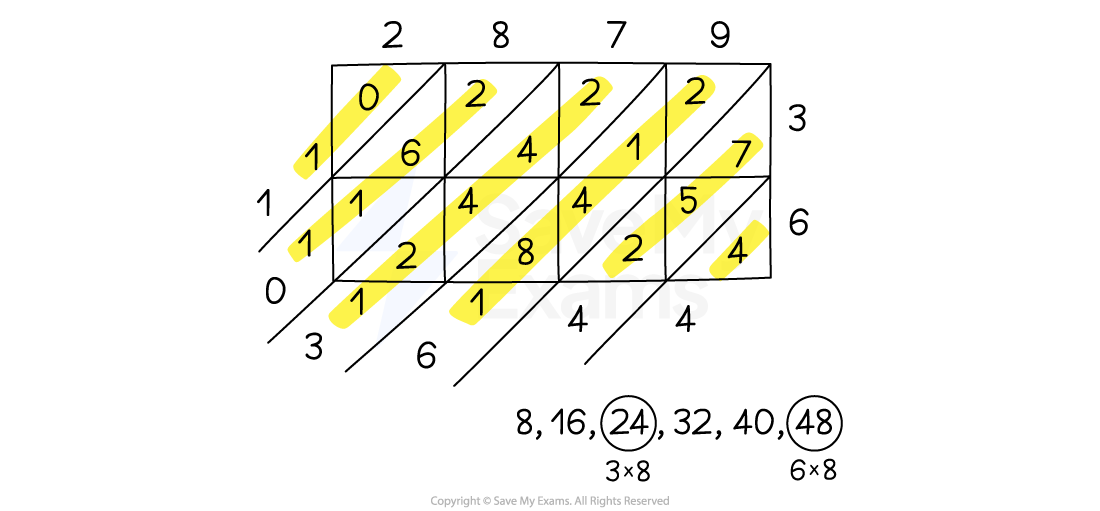
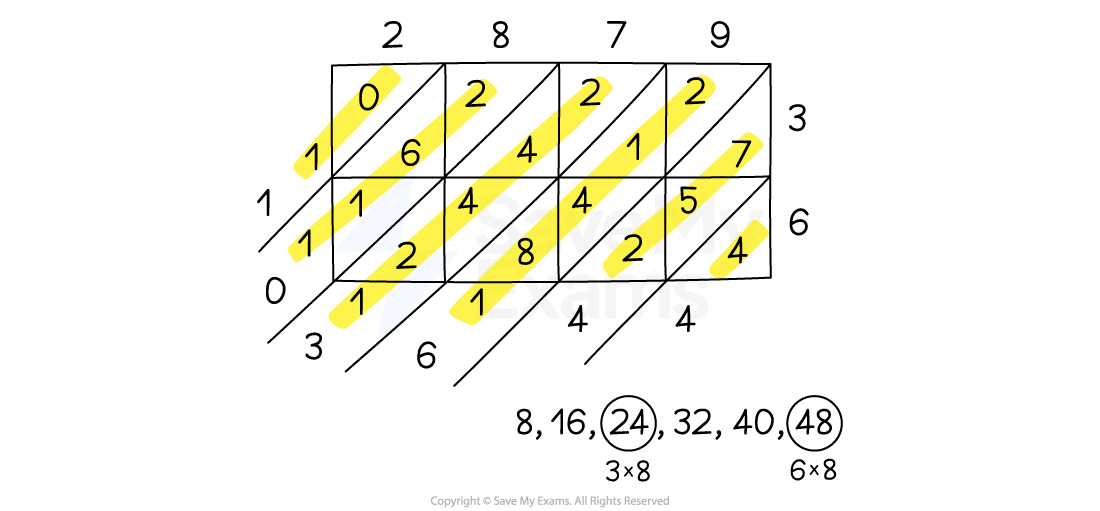
• To use the lattice method:

  • Draw a grid

    • The number of rows should be the same as the number of digits in one number

    • The number of columns should be the same as the number of digits in the other number

    • Draw diagonal lines through the boxes

  • Multiply each pair of digits, writing the result in the relevant box

    • Ones should be written in the bottom half of the box and tens in the top half of the box

  • Add the digits along the diagonals and write the result in the diagonal outside the grid

    • Carry the tens of any 2 digit result into the next diagonal

• For example, 3516 × 23 = 80 868

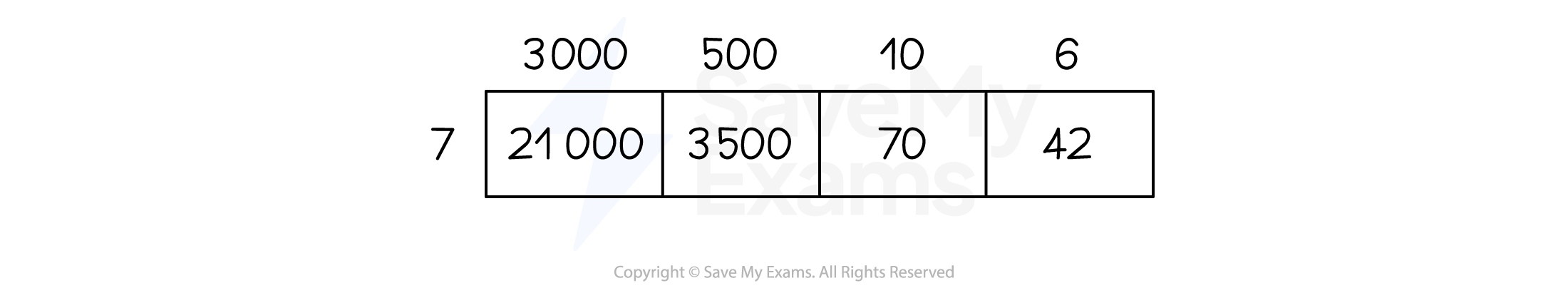
How do I use the grid method?

• This method keeps the value of the larger number intact

  • It may take longer with two larger numbers

  • Be careful lining up numbers with lots of zeros!

• To use the grid method

  • Draw a grid

    • The number of rows should be the same as the number of digits in one number

    • The number of columns should be the same as the number of digits in the other number

  • Label the rows and columns with the values of each digit

    • E.g. For 3516 you would use 3000, 500, 10 and 6

  • Multiply together the relevant values and put the results in the boxes

  • Add up all of the cells in the boxes 

• For example, 3516 × 7 = 24 612

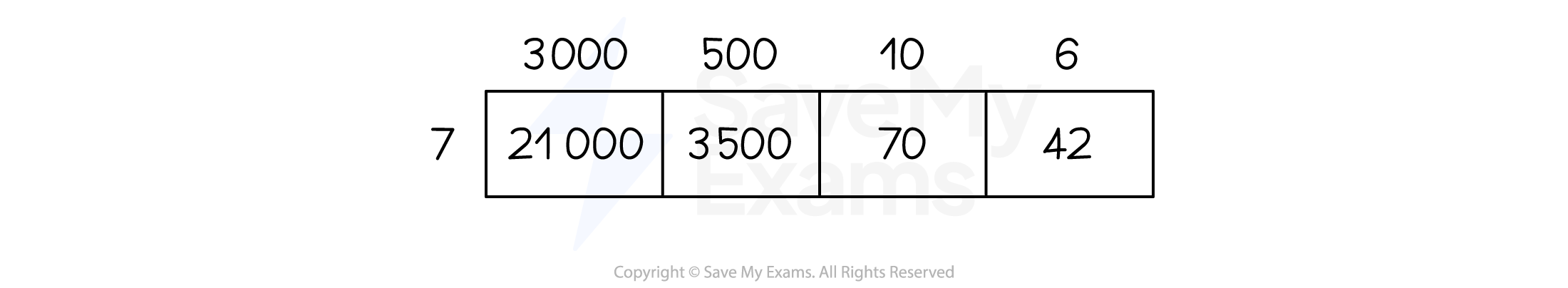
How do I use the repeated addition method?

• This is best for smaller, simpler cases

  • You may have seen this called ‘chunking’

• To use the repeated addition method

  • Build up to the answer using simple multiplication facts that can be worked out easily

  • To find 13 × 23 :
    1 × 23 = 23

    2 × 23 = 46

    4 × 23 = 92

    8 × 23 =184

  • So, 13 × 23 = 1 × 23 + 4 × 23 + 8 × 23 = 23 + 92 + 184 = 299

What words are used for multiplication and division?

• Multiplication may be phrased using the words lots of, times or product

• Division may be phrased using the words quotient, share and per

Division

How do I divide a number by another without a calculator?

• The most common written method for division is short division (or "the bus stop method")

  • There are other methods such as long division, but short division is generally the most efficient

• While short division is best when dividing by a single digit, for bigger numbers you may need a different approach

• You can use other number skills to help

  • eg. cancelling fractions, “shortcuts” for dividing by 2 and 10, and the repeated addition (“chunking”) method covered in Multiplication

Short division (bus stop method)

• Unless you can use simple shortcuts such as dividing by 2 or by 10, this method is best used when dividing by a single digit

• To find 174 ÷ 3

  • Starting from the left; 3 fits into 1, 0 times, with a remainder of 1

    • Carry the remainder of 1 over to the next digit, which forms 17

    • 

  • 3 fits into 17, 5 times, with a remainder of 2

    • Carry the remainder of 2 over to the next digit, which forms 24

    • 

  • 3 fits into 24, 8 times, with no remainder

    • 

  • So, 174 ÷ 3 = 58

Factoring & cancelling

• This involves treating division as you would if you were asked to simplify fractions

  • For example, 1008 ÷ 28 can be written as

  • This can then be simplified

    • 

    • 252 ÷ 7 can then be calculated using short division; the answer is 36

Dividing by 10, 100, 1000, … (Powers of 10)

• This is a case of shifting digits along the place value columns

  For example

  • 380 ÷ 10 = 38.0 (shifts by 1 column)

  • 45 ÷ 100 = 0.45 (shifts by 2 columns)

  • 28 ÷ 1000 = 0.028 (shifts by 3 columns)

    • For cases like this, it can help to add leading zeros

    • 0028 ÷ 1000 may be easier to visualise