Revision NotesExam QuestionsFlashcardsPast PapersMock Exams
IBMathsDPAnalysis & Approaches (AA)SLRevision Notes2. FunctionsQuadratic Functions & GraphsCompleting the Square

Completing the Square (DP IB Analysis & Approaches (AA)): Revision Note

Dan Finlay

Written by: Dan Finlay

Reviewed by: Jamie Wood

Updated on

DP Analysis & Approaches (AA): SLDP Analysis & Approaches (AA): HLDP Analysis & Approaches (AA): HLDP Analysis & Approaches (AA): SL

Did this video help you?

Completing the Square

Why is completing the square for quadratics useful?

  • Completing the square gives the maximum or minimum of a quadratic function

    • This can be used to define the range of the function

  • It gives the vertex when drawing the graph

  • It can be used to solve quadratic equations

  • It can be used to derive the quadratic formula

How do I complete the square for a monic quadratic of the form x2+bx+c?

  • Halve the value of b and write down stretchy left parenthesis x plus b over 2 stretchy right parenthesis squared

    • This is because stretchy left parenthesis x plus b over 2 stretchy right parenthesis squared equals x squared plus b x plus open parentheses b over 2 close parentheses squared, so it is similar to x squared plus b x plus c

  • Subtract the unwanted open parentheses b over 2 close parentheses squared term and add on the constant c

    • stretchy left parenthesis x plus b over 2 stretchy right parenthesis squared minus open parentheses b over 2 close parentheses squared plus c

How do I complete the square for a non-monic quadratic of the form ax2+bx+c?

  • Factorise out the a from the terms involving x

    • a stretchy left parenthesis x squared plus b over a x stretchy right parenthesis plus c 

    • Leaving the c un-factorised will avoid working with lots of fractions

  • Complete the square on the quadratic term inside the bracket

    • Halve b over a and write stretchy left parenthesis x plus fraction numerator b over denominator 2 a end fraction stretchy right parenthesis squared

      • This is because stretchy left parenthesis x plus fraction numerator b over denominator 2 a end fraction stretchy right parenthesis squared equals x squared plus b over a x plus open parentheses fraction numerator b over denominator 2 a end fraction close parentheses squared

    • Subtract the unwanted open parentheses fraction numerator b over denominator 2 a end fraction close parentheses squared term

  • Multiply through by a and add on c

    • a stretchy left square bracket stretchy left parenthesis x plus fraction numerator b over denominator 2 a end fraction stretchy right parenthesis squared minus open parentheses fraction numerator b over denominator 2 a end fraction close parentheses squared stretchy right square bracket plus c

    • a stretchy left parenthesis x plus fraction numerator b over denominator 2 a end fraction stretchy right parenthesis squared minus fraction numerator b squared over denominator 4 a end fraction plus c

Examiner Tips and Tricks

Some questions may not use the phrase "completing the square" so ensure you can recognise a quadratic expression or equation written in the form a left parenthesis x minus h right parenthesis squared plus k space left parenthesis equals 0 right parenthesis

Worked Example

Complete the square on the following expressions.

(i) x squared minus 8 x plus 3.

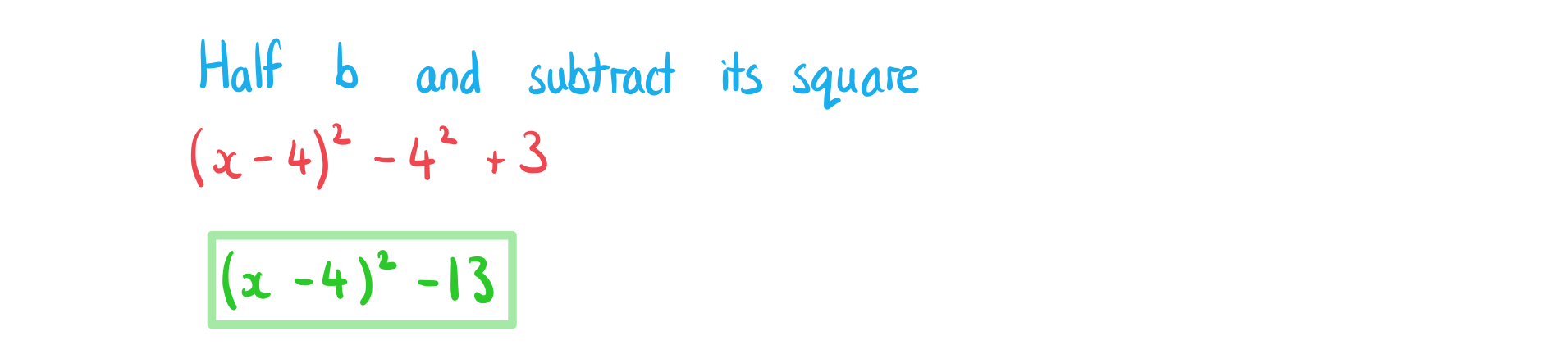
2-2-2-ib-aa-sl-complete-square-a-we-solution

(ii) 3 x squared plus 12 x minus 5.

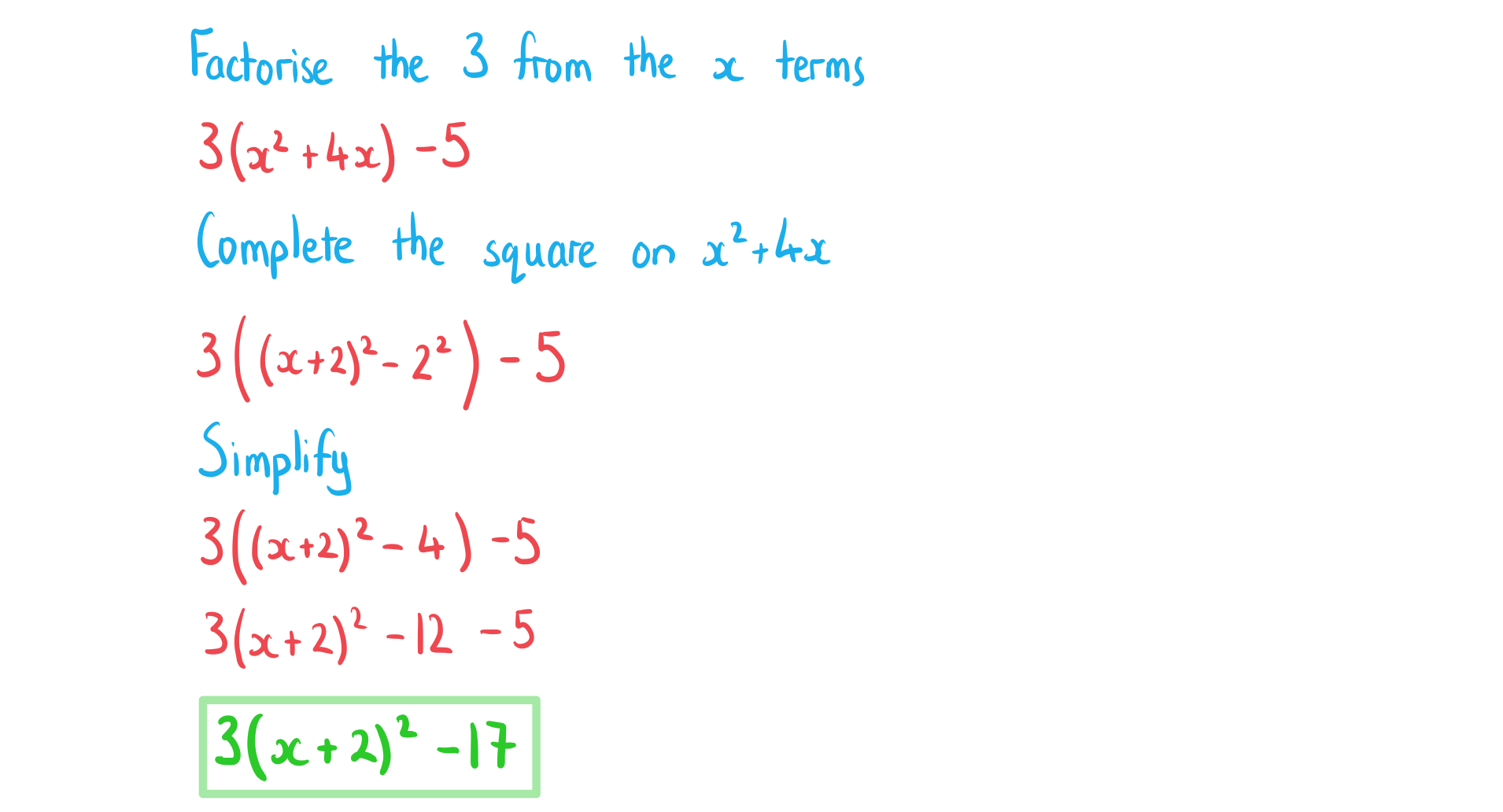
2-2-2-ib-aa-sl-complete-square-b-we-solution

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Factorising QuadraticsNext:Solving Quadratic Equations
    Author
    Reviewer
    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

    Jamie Wood

    Reviewer: Jamie Wood

    Expertise: Maths Content Creator

    Jamie graduated in 2014 from the University of Bristol with a degree in Electronic and Communications Engineering. He has worked as a teacher for 8 years, in secondary schools and in further education; teaching GCSE and A Level. He is passionate about helping students fulfil their potential through easy-to-use resources and high-quality questions and solutions.