GCSEFurther MathsAQARevision Notes6. GeometryTrigonometric Graphs & EquationsSolving Trig Equations

Solving Trig Equations (AQA GCSE Further Maths): Revision Note

Paul

Written by: Paul

Reviewed by: Dan Finlay

Updated on

Solving Basic Trig Equations

What are basic trig equations?

  • The types of equations dealt with here are those of the form

    • sin space x equals k

    • cos space x equals k

    • tan space x equals k

    • where k is a constant

  • (Most) scientific calculators will give you an answer to this type of equation

    • using inverse sin/cos/tan

      • e.g. x equals sin to the power of negative 1 end exponent space open parentheses k close parentheses

    • but trig equations usually have more than one solution

  • For inverse sin (sin-1) and inverse tan (tan-1)

    • (most) calculators will give an answer between -90° and 90°

  • For inverse cos (cos-1)

    • (most) calculators will give an answer between 0° and 180°

  • A question may require answers beyond these ranges

    • Typically, answers between 0° and 360° are required 

    • The properties (in particular, symmetry) of the trig graphs allow us to find all answers to trig equations

How are trigonometric equations of the form sin x = k solved?

  • The solutions to the equation sin x = 0.5 in the range 0° < x < 360° are x = 30° and x = 150°

    • If you like, check on a calculator that both sin 30° and sin 150° give 0.5

  • The first solution comes from your calculator (by taking inverse sin of both sides)

    • x = sin-1 (0.5) = 30°

  • The second solution comes from the symmetry of the graph y = sin x between 0° and 360°

    • Sketch the graph

    • Draw a vertical line from x = 30° to the curve, then horizontally across to another point on the curve, then vertically back to the x-axis again

    • By the symmetry of the curve, the new value of x is 180° - 30° = 150°

  • In general, if x° is an acute angle that solves sin x = k, then 180° - x° is the obtuse angle that solves the same equation

  • If/when a calculator gives x as a negative value when using inverse sin

    • extend your graph sketch for negative values of x (i.e. to the left of the y-axis)

cie-igcse-3-12-2-solving-trig-equations-1

How are trigonometric equations of the form cos x = k solved?

  • The solutions to the equation cos x = 0.5 in the range 0° < x < 360° are x = 60° and x = 300°

    • If you like, check on a calculator that both cos 60° and cos 300° give 0.5

  • The first solution comes from your calculator (by taking inverse cos of both sides)

    • x = cos-1 (0.5) = 60°

  • The second solution comes from the symmetry of the graph y = cos x between 0° and 360°

    • Sketch the graph

    • Draw a vertical line from x = 60° to the curve, then horizontally across to another point on the curve, then vertically back to the x-axis again

    • By the symmetry of the curve, the new value of x is 360° - 60° = 300°

  • In general, if x° is an angle that solves cos x = k, then 360° - x° is another angle that solves the same equation

  • (Most) calculators will not give x as a negative value when using inverse cos

cie-igcse-3-12-2-solving-trig-equations-2

How are trigonometric equations of the form tan x = k solved?

  • The solutions to the equation tan x = 1 in the range 0° < x < 360° are x = 45° and x = 225°

    • Check on a calculator that both tan 45° and tan 225° give 1

  • The first solution comes from your calculator (by taking inverse tan of both sides)

    • x = tan-1(1) = 45°

  • The second solution comes from the symmetry of the graph y = tan x between 0° and 360°

    • Sketch the graph

    • Draw a vertical line from x = 45° to the curve, then horizontally across to another point on the curve (a different “branch” of tan x), then vertically back to the x-axis again

    • The new value of x is 45° + 180° = 225° as the next “branch” of tan x is shifted 180° to the right

  • In general, if x° is an angle that solves tan x = k, then x° + 180° is another angle that solve the same equation

  • If/when a calculator gives x as a negative value when using inverse tan

    • extend your graph sketch for negative values of x (i.e. to the left of the y-axis)

cie-igcse-3-12-2-solving-trig-equations-3

Examiner Tips and Tricks

  • Use a calculator to check your solutions by substituting them into the original equation

    • e.g. 60° is a correct solution of cos x = 0.5 as cos 60° = 0.5 on a calculator
      but 330° is an incorrect solution as cos 330° ≠ 0.5

Worked Example

Solve sin x = 0.25 in the range 0° < x < 360°, giving your answers correct to 1 decimal place 

Use a calculator to find the first solution (by taking inverse sin of both sides)

x = sin-1(0.25) = 14.4775… = 14.48° to 2 dp

Sketch the graph of y = sin x and mark on (roughly) where x = 14.48 and y = 0.25 would be
Draw a vertical line up to the curve, then horizontally across to the next point on the curve, then vertically back down to the x-axis

cie-igcse-3-12-2-solving-trig-equations-4

Find this value using the symmetry of the curve (by taking 14.48 away from 180)

180° – 14.48° = 165.52°

Give both answers correct to 1 decimal place

x = 14.5° or x = 165.5°

Solving Quadratic Trig Equations

What is a quadratic trig equation?

  • A quadratic trig equation will have a 'squared' term involved in it

    • this will be either sin2x, cos2x or tan2x

    • there may be terms involving sin x, cos x or tan x as well

      • and possibly a constant term (i.e. a number)

  • Quadratic trig equations are very similar to normal quadratic equations

    • but the 'x' is replaced by 'sin x' (or 'cos x' or 'tan x')

  • Recall from the work on trig identities that sin2x means the same as (sin x)2

    • and likewise for cos/tan

How do I solve quadratic trig equations?

  • When first practising solving quadratic trig equations it may be helpful to replace sin x, cos x or tan x by a letter, y say

    • e.g. for the quadratic trig equation tan squared space x equals 8 tan space x minus 7 replacing "tan x" with "y" gives y squared equals 8 y minus 7

    • if you know what "hidden quadratics" are, this is the same process

  • Solve the quadratic equation as you normally would

    • the equation may need rearranging so it is in quadratic form

      • " a x squared plus b x plus c equals 0 "

      • e.g.  y squared minus 8 y plus 7 equals 0

    • solving the equation may involve factorising, completing the square or the quadratic formula

  • The answer(s) to the quadratic equation will not be the values for x (they are the values of y)

    • i.e.  they are the values of sin x, cos x or tan x

      • y = tan x in our example

  • Replace y with its trig function to form two basic trig equations to solve to find the values of x

    • e.g.  tan space x equals 7 and tan space x equals 1

    • Using inverse tan, the values for x in the range 0 degree less or equal than x degree less or equal than 180 degree are x equals 81.9 (1 d.p.) and x equals 45

    • Sketching the graph of y equals tan space x between 0° and 360° shows the other two solutions

      • x equals 81.9 plus 180 equals 261.9 degree and x equals 45 plus 180 equals 225 degree

  • In harder problems, one of the basic trig equations may have no possible solutions

    • e.g. cos space x equals 2

      • The graph y = cos x is always between -1 to 1 on the y-axis, so this trig equation has no solutions

Worked Example

Solve the equation 4 sin squared space x minus 1 equals 0 for 0 degree less or equal than x degree less or equal than 360 degree, giving your answers for x as exact values. 

Let y = sin x and rewrite the equation in y

4 y squared minus 1 equals 0 

This equation can be solved by rearranging to y squared equals 1 fourthbut you must remember plus-or-minus square root of blank end root)
A neater way to get two solutions is to use the difference of two squares

open parentheses 2 y minus 1 close parentheses open parentheses 2 y plus 1 close parentheses equals 0 

Solve the factorised equation (by setting each bracket equal to zero)

y equals 1 half or y equals negative 1 half 

Replace the y with sin x

sin space x equals 1 half or sin space x equals negative 1 half 

Write out the "first half" of this problem and solve it

sin space x space equals 1 half where 0 degree less than x less than 360 degree 

Use a calculator (or your knowledge of exact trig values) to find inverse sin

sin to the power of negative 1 end exponent open parentheses 1 half close parentheses equals 30 

Use a sketch of y equals sin space x to find the other solution (by symmetry

cie-igcse-3-12-2-solving-trig-equations-1

 Write out the two solutions so far

x = 30° or x = 150° 

Now write out the "second half" of this problem and solve it

sin space x equals negative 1 half where 0 degree less than x less than 360 degree 

From extending the sketch above in the negative x-axis, or using sin to the power of negative 1 end exponent open parentheses negative 1 half close parentheses, the first negative solution is

x = -30° 

But this is not in the range 0° to 360°
Adding 30° to 180° and subtracting 30° from 360° would give the correct values

x = 180° + 30° = 210° or x = 360° - 30° = 330° 

Combine these two solutions with the two found previously
It is good practice to write final solutions out in numerical order

x = 30, 150, 210, 330

Solving Trig Equations with Identities

How do I use trig identities to help solve trig equations?

  • In general, trig equations are easiest to solve when they involve one out of sin x, cos x or tan x only

  • For some equations involving different trig functions, you can often rewrite them back in terms of one only

    • To do this, use one (or both) of the identities

      • tan space theta identical to fraction numerator sin space theta over denominator cos space theta end fraction or sin squared space theta plus cos squared space theta identical to 1

  • The majority of questions will involve the second identity as this is frequently used with quadratic trig equations

    • It will be used in one of its rearranged forms

      • sin squared space theta equals 1 minus cos squared space theta or cos squared space theta equals 1 minus sin squared space theta

      • which will replace sin squared space theta terms (with cos2 ...) and cos squared space theta terms (with sin2 ...) respectively

      • choose whichever suits the question

      • e.g. The equation cos squared space x minus 3 sin space x plus 1 equals 0 can be rewritten as open parentheses 1 minus sin squared space x close parentheses minus 3 sin space x plus 1 equals 0
        which involves sin x terms only and so is easier to solve (after some rearranging)

  • The tan space theta identity is used less frequently and would normally appear in reverse

    • e.g. The equations fraction numerator sin space x over denominator cos space x end fraction equals 3 over 4 or  4 sin space x equals 3 space cos space x or 3 cos space x minus 4 space sin space x equals 0 etc can be rewritten as tan space x equals 3 over 4

    • this can be solved using a calculator and the graph of y equals tan space x

Examiner Tips and Tricks

  • Write out both identities for any trig equation questions in case they help

  • Sketch the appropriate graph

    • y = sin x, y = cos x or y = tan x

    • use the graph to ensure you find ALL solutions within the given interval

    • this is particularly important when a calculator gives an initial negative answer

Worked Example

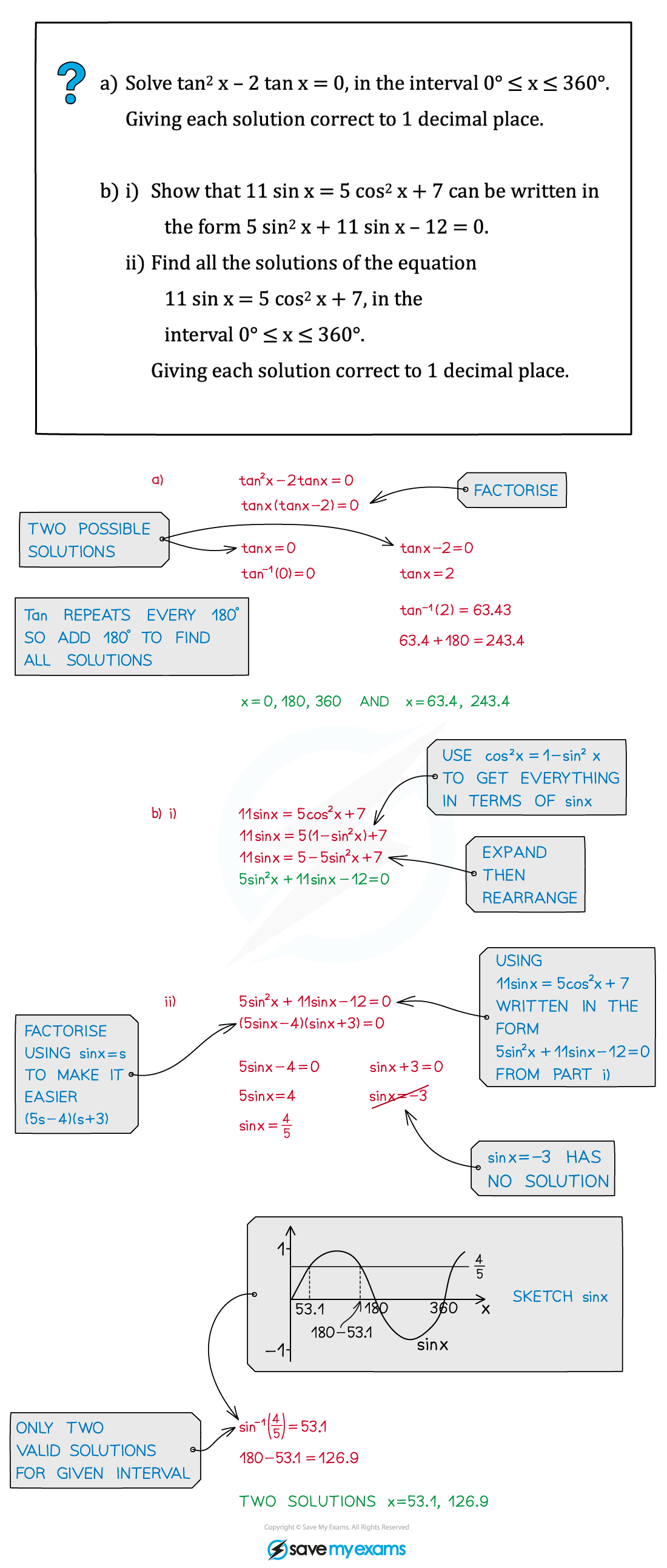
Quadratic Trigonometric Equations Example Solution, A Level & AS Level Pure Maths Revision Notes

Worked Example

Solve the equation 3 cos space x equals 9 space sin space x minus 6 cos space x for 0 degree less or equal than x degree less or equal than 360 degree.

Add 6cos x to both sides to bring the cos x terms together 

9 space cos space x equals 9 space sin space x 

Divide both sides by 9

cos space x equals sin space x 

By considering the identity tan space x equals fraction numerator sin space x over denominator cos space x end fraction, divide both sides by cos x

fraction numerator cos space x over denominator cos space x end fraction equals fraction numerator sin space x over denominator cos space x end fraction 

Cancel the left-hand side (this does not cancel to give zero)

1 equals fraction numerator sin space x over denominator cos space x end fraction 

Use the identity tan space x equals fraction numerator sin space x over denominator cos space x end fraction to rewrite the right-hand side as tan x

1 equals tan space x 

The problem is now to solve the following

tan italic space x equals 1 where 0 degree less than x less than 360 degree 

Use tan to the power of negative 1 end exponent open parentheses 1 close parentheses, or your knowledge of exact trig values, to find the first x solution

x = 45 

Sketch the graph of y = tan x to find the other solution 

cie-igcse-3-12-2-solving-trig-equations-3

Write the two solutions in numerical order

x = 45 or x = 225

👀 You've read 1 of your 5 free revision notes this week
An illustration of students holding their exam resultsUnlock more revision notes. It's free!

By signing up you agree to our Terms and Privacy Policy.

Already have an account? Log in

Test yourself

Did this page help you?

Previous:Trigonometric Identities
Author
Reviewer
Paul

Author: Paul

Expertise: Maths Content Creator

Paul has taught mathematics for 20 years and has been an examiner for Edexcel for over a decade. GCSE, A level, pure, mechanics, statistics, discrete – if it’s in a Maths exam, Paul will know about it. Paul is a passionate fan of clear and colourful notes with fascinating diagrams.

Dan Finlay

Reviewer: Dan Finlay

Expertise: Maths Subject Lead

Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

Download notes on Solving Trig Equations