Resistance in Series & Parallel (Edexcel International A Level (IAL) Physics): Revision Note
Exam code: YPH11
Deriving Equations for Resistance in Series & Parallel
Resistors In Series
When two or more components are connected in series:
The combined resistance of the components is equal to the sum of individual resistances
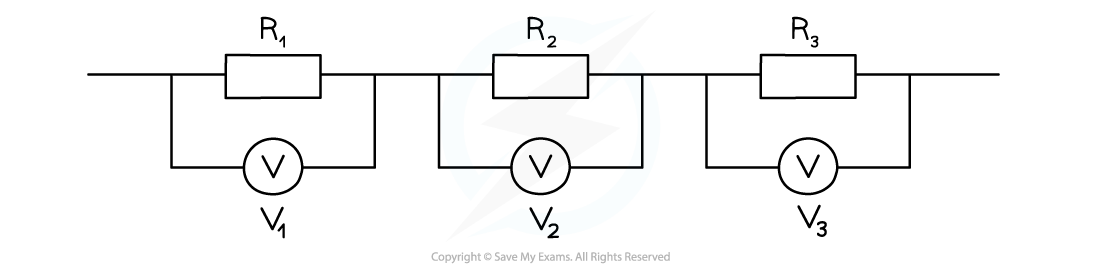
Resistors connected in series
The equation for combined resistors in series is derived using the electric current rule and the electrical voltages rule
These rules describe that for a series circuit:
The current is the same through all resistors
The potential difference is split between all the resistors

The equation for the combined resistance of resistors in series is therefore:

Resistors In Parallel
In a parallel circuit, the combined resistance of the components requires the use of reciprocals
The reciprocal of the combined resistance of two or more resistors is the sum of the reciprocals of the individual resistances

Resistors connected in parallel
The equation for combined resistors in parallel is derived using the electric current rule and the electrical voltages rule
These rules describe that for a parallel circuit:
The current is the split at the junction (and therefore between resistors)
The potential difference is the same across all resistors

The equation for the combined resistance of resistors in parallel is therefore:

This means the combined resistance decreases
The combined resistance is less than the resistance of any of the individual components
For example, If two resistors of equal resistance are connected in parallel, then the combined resistance will halve
Using Equations for Resistance in Series & Parallel
Series Circuits
Worked Example
The combined resistance R in the following series circuit is 60 Ω.
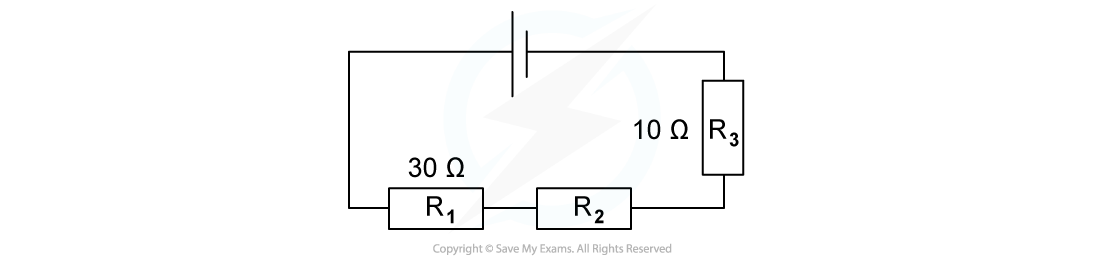
Wich of the following is the value of R2?
A. 100 Ω
B. 30 Ω
C. 20 Ω
D. 40 Ω

Parallel Circuits
Worked Example
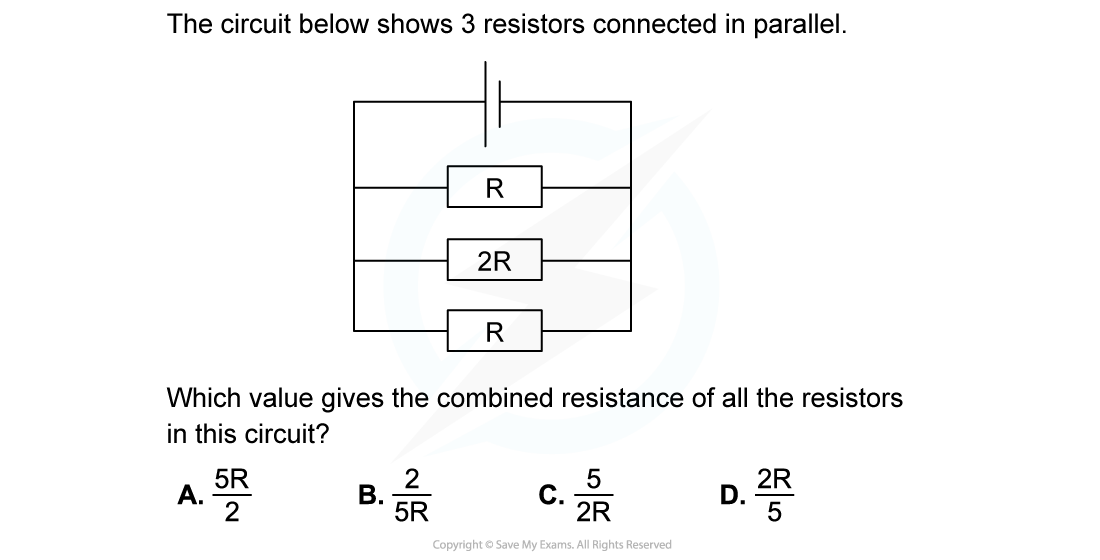

Examiner Tips and Tricks
The most common mistake is to forget to find the correct value for RT in parallel. Remember to do to get the correct value.
Reciprocals can be considered in the following way:
The reciprocal of a value is
For example, the reciprocal of a whole number such as 2 equals
The reciprocal of
is 2
If the number is already a fraction, the numerator and denominator are ‘flipped’ round

The reciprocal of a number is 1 ÷ number
In the case of the resistance R, this becomes
To get the value of R from
, you must do
You can also use the reciprocal button on your calculator (labelled either x-1 or
, depending on your calculator)

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?