Centripetal Force (Edexcel International A Level Physics)

•  Centripetal force can be calculated using any of the following equations:

• Where:
  • F = centripetal force (N)
  • v = linear velocity (m s^-1)
  • ⍵ = angular speed (rad s^-1)
  • r = radius of the orbit (m)

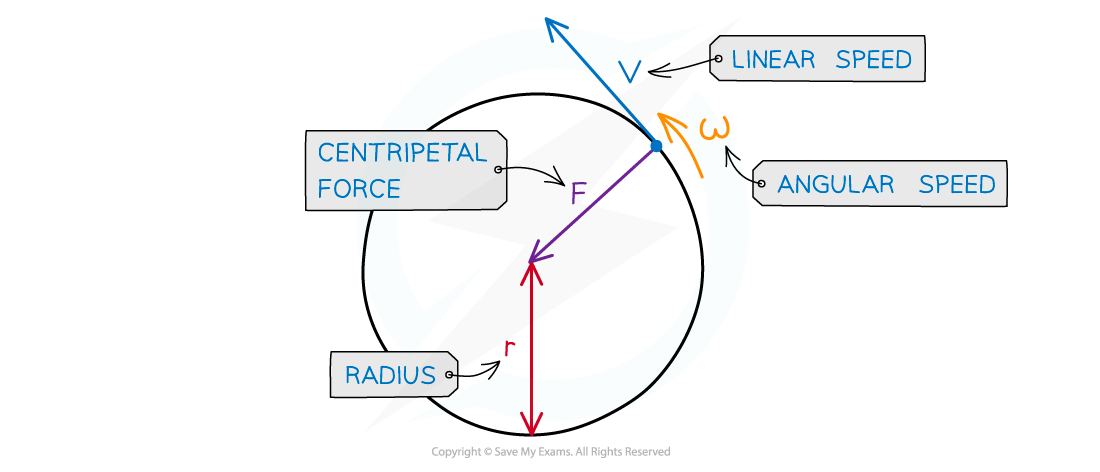
Centripetal force is always perpendicular to the direction of travel

• The centripetal force is the resultant force on the object moving in a circle
  • This is particularly important if there are multiple forces on the object, such as weight

Vertical Circular Motion

• An example of vertical circular motion is swinging a ball on a string in a vertical circle
• The forces acting on the ball are:
  • The tension in the string
  • The weight of the ball downwards

• As the ball moves around the circle, the direction of the tension will change continuously
• The magnitude of the tension will also vary continuously, reaching a maximum value at the bottom and a minimum value at the top
  • This is because the direction of the weight of the ball never changes, so the resultant force will vary depending on the position of the ball in the circle

• At the bottom of the circle, the tension must overcome the weight, this can be written as:

• As a result, the acceleration, and hence, the speed of the ball will be slower at the top
• At the top of the circle, the tension and weight act in the same direction, this can be written as:

• As a result, the acceleration, and hence, the speed of the ball will be faster at the bottom

Step 1: Draw the forces on the bucket at the top

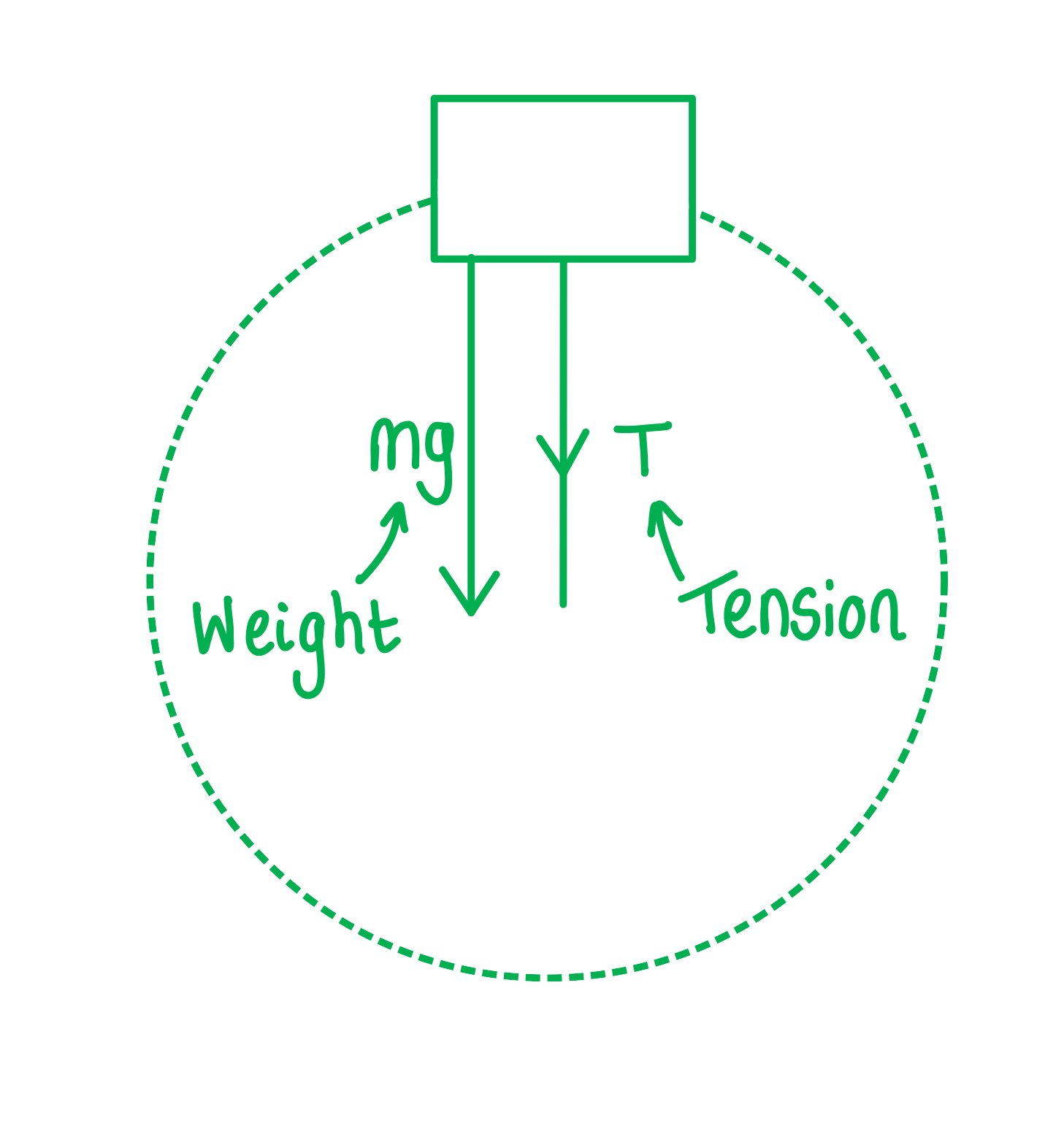
Step 2: Write an expression for the centripetal force

• • The weight of the bucket = mg
  • At the top of the circular path, the weight and tension act in the same direction, so the centripetal force is

• • The minimum speed v is when the string is taut but not stretched, so the tension here is zero (T = 0)

Step 3: Rearrange for velocity v and calculate

• • m cancels from both sides