Interpreting Graphs (Edexcel International A Level (IAL) Physics): Revision Note
Exam code: YPH11
Relationships between Variables
Identifying the relationship between two variables shows how one variable changes with another
This is best figured out from an equation that links both variables together
Two variables can be:
Directly proportional
Inversely proportional
For two variables, y and x that are directly proportional, their relationship looks like:
y ∝ x
This means that as y increases, x also increases at the same rate (and vice versa)
An example of this is
F = ma
Since m is a constant, F and a are directly proportional
If a is doubled, then so is F
For two variables, y and x that are inversely proportional, this looks like:
y ∝
This means that as y increases, x decreases at the same rate (or vice versa)
An example of this is
R =
If V is constant, then R and I are inversely proportional
If I is doubled, the R is halved
It is important to note that in both of these examples, the remaining variable is constant, this is important to consider and check before stating the relationship between two variables
In F = ma, if m changed as well with a then F would not increase by the same amount as a (i.e. it would no longer be directly proportional)
Therefore, the directly proportional relationship can be turned into an equation by replacing '∝' with an '=' sign, and adding a constant k
y = kx
This now means that as y increases, x increases with the amount determined by the constant k
If k is 3 then y = 3x so the both increase by a factor of 3
The same happens for an inversely proportional relationship
y =
This now means that as y increases, x increases with the amount determined by the constant k
If k is 3 then y =
so y decreases by a factor of 3
Another common relationship is the inverse square law
For two variables, y and x that are related by the inverse square law, this looks like:
y ∝
This means that if x increases by a factor of 2, then y decreases by a factor of 22 = 4!
An example of this is
F =
If L is constant, then d and F are inversely proportional
If the distance d is 3 times larger, then the flux intensity, F is 32 = 9 times smaller
Worked Example
A student collects the following data of the count rate on a geiger counter increasing in distance from a gamma ray source.
Distance d / cm | Count rate C / counts min-1 |
10 | 512 |
20 | 128 |
30 | 57 |
40 | 32 |
Show that the relationship between distance and count rate is an inverse square law relationship.
Answer:
Step 1: State the inverse square law relationship
The count rate is inversely proportional to the distance squared
C ∝
Step 2: Change relationship into an equation
C =
Step 3: Rearrange for constant, k
k = Cd2
Step 4: Show all pairs of C and d have the same constant, k
Row 1: k = 512 × (10)2 = 51200
Row 2: k = 128 × (20)2 = 51200
Row 3: k = 57 × (30)2 = 51300
Row 4: k = 32 × (40)2 = 51200
Step 5: Comment on constant and refer back to relationship
Since all values have the same constant k to 2 significant figures (51000), C and d have an inverse square law relationship
Examiner Tips and Tricks
When you're comparing two variables you must check whether the other variables are constant before declaring that they're inversely or directly proportional. Otherwise, one will not increase at the same rate as the other, which goes against the definition!
Determining Constants from Graphs
Straight line graphs (linear relationships) are common in A-level physics
These graphs are useful because we can calculate a constant value from them
This is the gradient
The gradient can be calculated by dividing the rise (change in y) by the run (change in x)
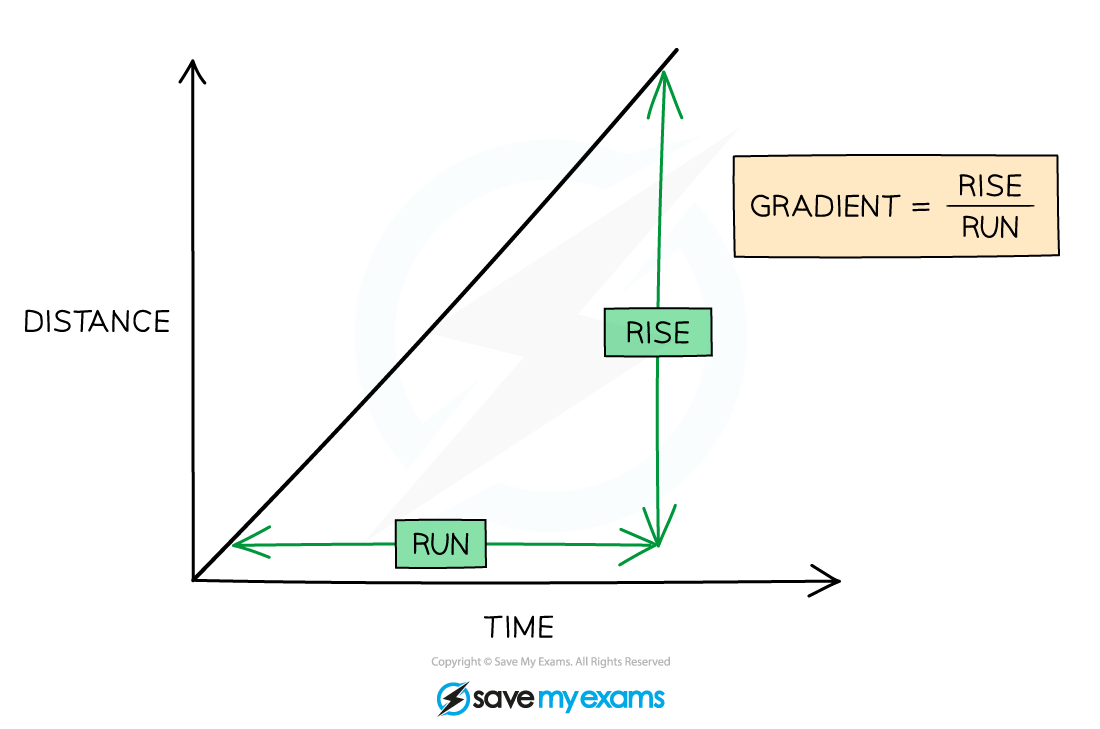
The full calculation of the gradient needs to be shown in the working out, including the correct substitution of identified plotted points from the axes into the equation
The triangle used to calculate the gradient should be drawn on the graph and it needs to be as large as possible
Small triangles are not acceptable for working out a gradient
When using the results from a table of values, the triangle that is used to obtain the gradient can utilise points that lie on the line of best fit but not values that lie away from the line
Try to avoid using data points to calculate this where possible
The units of the gradient will be the ratio of the units of the y variable and units of the x variable
E.g., For a graph for extension x (in m) against force F (in N) the units of the gradient would be N m-1
Worked Example
Calculate the gradient of the following graph.

Answer:
Step 1: Draw a large gradient triangle

Step 2: Use the gradient equation
Gradient = = = 15.7 Ω m-1
Examiner Tips and Tricks
The general rule is to draw a gradient triangle that takes up more than half of the graph. Drawing triangles too small, even if you get the correct answer, will not achieve full marks in the practical paper!
There is normally a range of answers accepted in the mark scheme for gradients, as everyone's line of best fit may be slightly different, but don't count on this! This range will often be very small so always use a sharp pencil and ruler to draw lines where possible. Show your working out on the paper always to help this.
Remember to always check the units and scale when reading values from a graph! Don't just assume that all lengths are in m or that forces will be in N. They could be in mm or kN. Also watch out for the powers of ten e.g., Force F × 103 / N which means a value of '5' on the graph will actually be 5 × 103 N (or 5 kN).

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?