IBMathsDPApplications & Interpretation (AI)HLRevision Notes2. FunctionsModelling with Logarithmic, Logistic & Piecewise FunctionsNatural Logarithmic Models

Natural Logarithmic Models (DP IB Applications & Interpretation (AI)) : Revision Note

Dan Finlay

Last updated

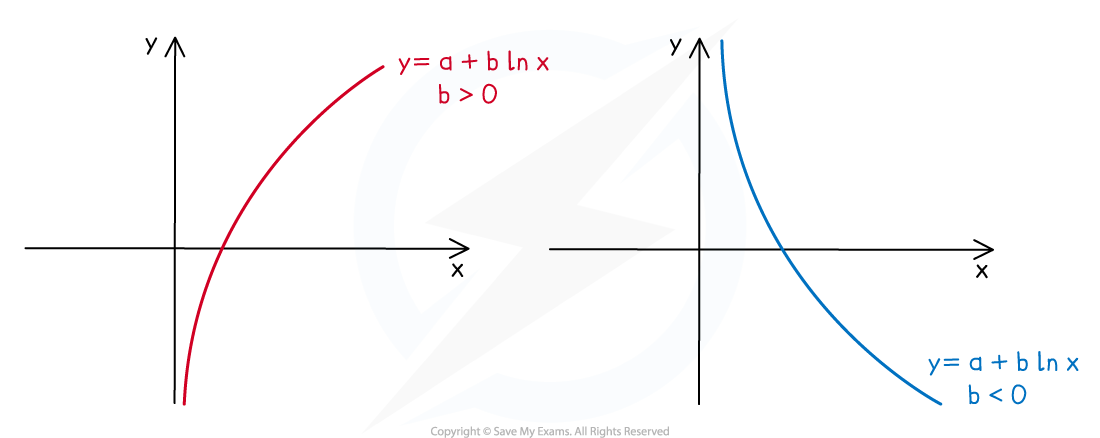
Natural Logarithmic Models

What are the parameters of natural logarithmic models?

  • A natural logarithmic model is of the form space f left parenthesis x right parenthesis equals a plus b space ln x

  • The a represents the value of the function when x = 1

  • The b determines the rate of change of the function

    • A bigger absolute value of b leads to a faster rate of change

What can be modelled as a natural logarithmic model?

  • A natural logarithmic model can be used when the variable increases rapidly for a period followed by a much slower rate of increase with no limiting value

    • M(I) is the magnitude of an earthquake with an intensity of I

    • d(I) is the decibels measured of a noise with an intensity of I

What are possible limitations a natural logarithmic model?

  • A natural logarithmic graph is unbounded

    • However in real-life the variable might have a limiting value

Worked Example

The sound intensity level, L, in decibels (dB) can be modelled by the function

L left parenthesis I right parenthesis equals a plus 8 ln I,

where I is the sound intensity, in watts per square metre (Wm-2).

a) Given that a sound intensity of 1 Wm-2 produces a sound intensity level of 110 dB, write down the value of a.

2-6-2-ib-ai-hl-natural-log-model-a-we-solution

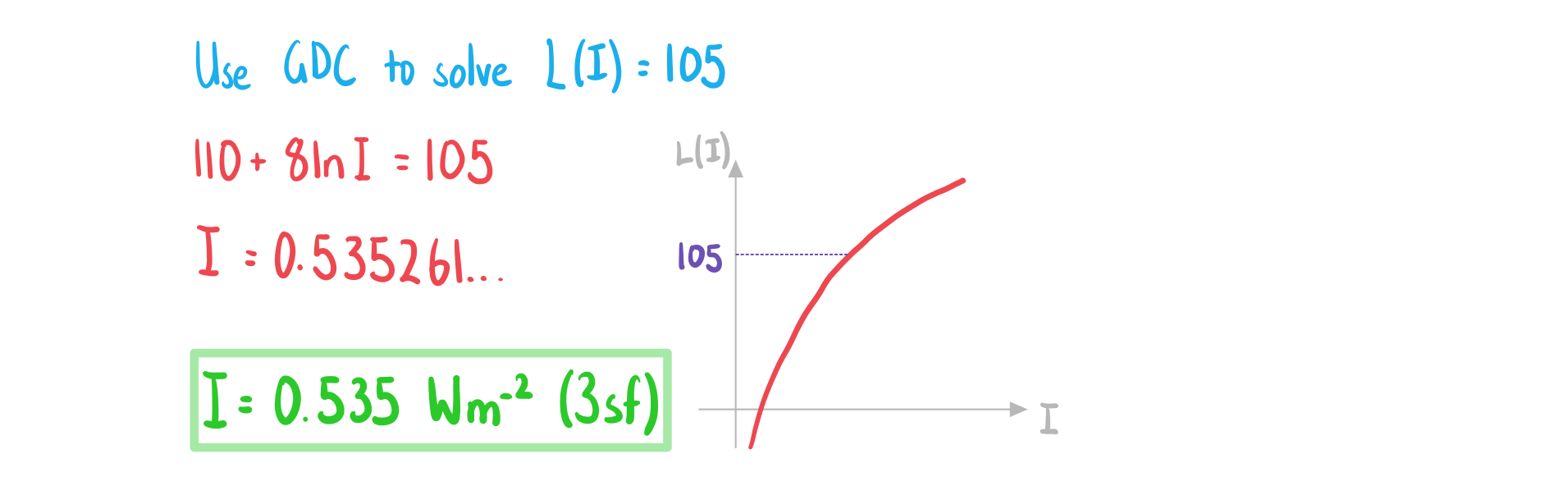
b) Find the sound intensity, in Wm-2, of a car alarm that has a sound intensity level of 105 dB.

2-6-2-ib-ai-hl-natural-log-model-b-we-solution

You've read 1 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

  • I would just like to say a massive thank you for putting together such a brilliant, easy to use website.I really think using this site helped me secure my top gradesin science and maths. You really did save my exams! Thank you.

    Beth
    IGCSE Student

  • This website is soooo useful and I can’t ever thank you enough for organising questions by topic like this. Furthermore, the name of the website could not have been more appropriate as it literally did SAVE MY EXAMS!

    Fathima
    A Level Student
Test yourselfFlashcards

Did this page help you?

Previous:Properties of Further GraphsNext:Logistic Models
Dan Finlay

Author: Dan Finlay

Expertise: Maths Lead

Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

Download notes on Natural Logarithmic Models