Inverse Functions (DP IB Applications & Interpretation (AI)): Revision Note

Inverse functions

What is an inverse function?

• An inverse function, , reverses (or undoes) the effect of

  • for example

    • if then

    • if then

• Inverse functions can be used to solve equations

  • e.g. the solution of  is 

What is the identity function?

• The identity function  maps each value to itself

  • 

    • e.g.

• Applying a function to an input

  • then applying the inverse,  

    • gives back the original input

• This also works if you swap the order of and  

  • i.e. the composite function

    • has the same effect as the identity function

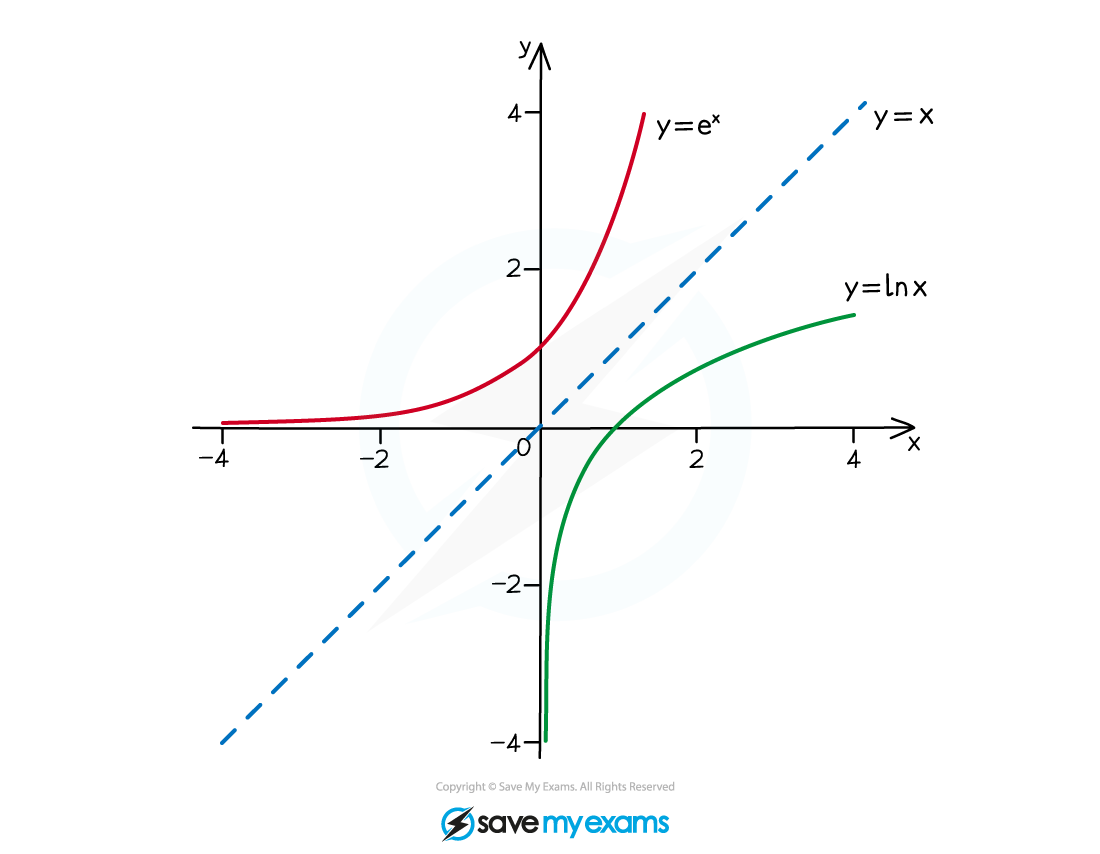
How do I sketch an inverse function?

• The graph of  is a reflection of the graph in the line 

  • e.g. if and

    • then and

    • which reflect in

• If intersects then also intersects at the same point

  • i.e. solutions to either  or 

    • are solutions to 

  • There may be other solutions to  that don't lie on the line 

How do I find the inverse of a function?

• To find the inverse function using algebra, following these steps:

• STEP 1
  Swap the and  in 

• STEP 2
  Rearrange  to make  the subject

  • The result is

How do I find the domain and range of an inverse function?

• The domain of a function becomes the range of its inverse

  • e.g. if has domain

    • then the range of is

• The range of a function becomes the domain of its inverse

  • e.g. if has range

    • then the domain of is

What condition is needed for an inverse function to exist?

• For an inverse function to exist

  • the original function must be one-to-one

• This ensures never gives out two or more outputs

  • which functions are not allowed to do

How do I restrict many-to-one functions to be one-to-one?

• To restrict the domain of a many-to-one function

  • choose a subset of the domain on which the function is one-to-one

    • e.g. restrict for the function to

    • or or or ... etc

• To find the biggest possible one-to-one domain:

• For quadratics

  • use the vertex as the upper or lower bound for the restricted domain

  • e.g.

    • or 

  • e.g.

    • or 

• For trigonometric functions

  • use part of a cycle

  • e.g.

    • 

  • e.g.

    • 

  • e.g. restrict the domain to one cycle between two asymptotes

    • 

How do I find the inverse function of a restricted function?

• This is best shown through an example

• e.g. to find the inverse of the function that has been restricted to the domain

  • use algebra initially

    • gives

    • so

  • then choose a sign depending on the range of the inverse

    • Use the rule that "the range of the inverse, is equals the domain of the function"

    • The domain of is

    • so is the range of

  • means the inverse function always gives positive outputs

    • so choose the positive square root out of

    • The answer is

• If the restricted domain is changed to

  • the inverse function changes to