Revision NotesExam QuestionsFlashcardsPast PapersMock Exams
IBMathsDPApplications & Interpretation (AI)HLRevision Notes3. Geometry & TrigonometryMatrix TransformationsDeterminant of a Transformation Matrix

Determinant of a Transformation Matrix (DP IB Applications & Interpretation (AI)): Revision Note

Paul

Written by: Paul

Reviewed by: Dan Finlay

Updated on

Determinant of a transformation matrix

What does the determinant of a transformation matrix represent?

  • The absolute value of the determinant of a transformation matrix is the area scale factor of the transformation

    • Area scale factor = vertical line det space bold italic T vertical line

  • The area of the image will be product of the area of the object and the absolute value of the determinant of the transformation matrix

    • Area space of space image space equals space vertical line det space bold italic T vertical line space cross times space Area space of space object

  • The area is unchanged if open vertical bar det bold space bold italic T close vertical bar equals 1

    • The area increases if open vertical bar det bold space bold italic T close vertical bar greater than 1

    • The area decreases if open vertical bar det bold space bold italic T close vertical bar less than 1

  • If the determinant is negative then the orientation of the shape will be reversed

    • For example, if the shape has been reflected

Examiner Tips and Tricks

Remember that the formula for finding the determinant of a matrix is given in the formula booklet. You can also use your GDC.

Worked Example

An isosceles triangle has vertices A(3, 1), B(15, 1) and C(9, 9).

a) Find the area of the isosceles triangle.

3-6-2-ib-hl-ai-only-we1a-soltn

b) Triangle △ABC is transformed using the matrix bold italic T equals open parentheses table row 3 2 row cell negative 1 end cell 2 end table close parentheses. Find the area of the transformed triangle.

3-6-2-ib-hl-ai-only-we1b-soltn

c) Triangle △ABC is now transformed using the matrix bold italic U equals open parentheses table row a cell negative 2 end cell row 3 cell a squared end cell end table close parentheses where a element of straight integer numbers. Given that the area of the image is twice as large as the area of the object, find the value of a.

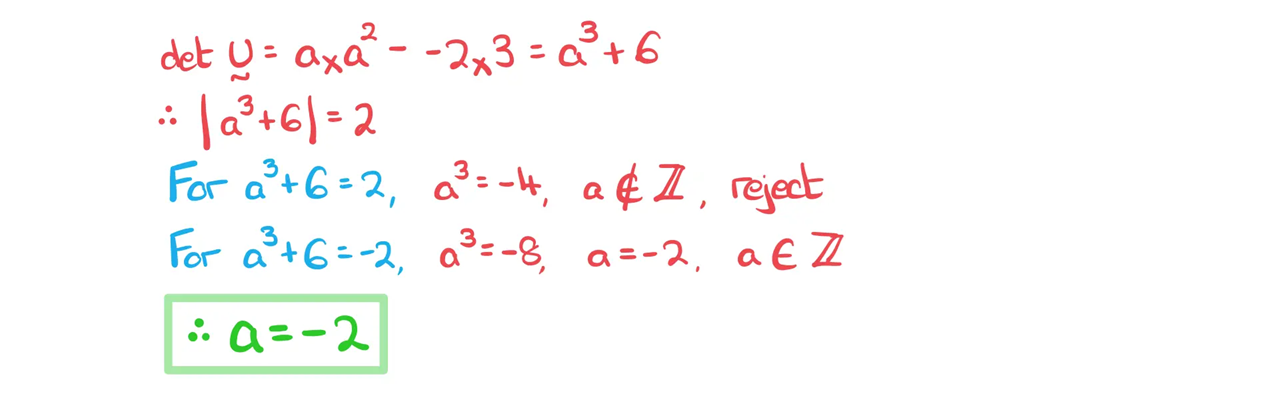
3-6-2-ib-hl-ai-only-we1c-soltn

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards
    Previous:Matrices of Composite TransformationsNext:Introduction to Vectors
    Author
    Reviewer
    Paul

    Author: Paul

    Expertise: Maths Content Creator

    Paul has taught mathematics for 20 years and has been an examiner for Edexcel for over a decade. GCSE, A level, pure, mechanics, statistics, discrete – if it’s in a Maths exam, Paul will know about it. Paul is a passionate fan of clear and colourful notes with fascinating diagrams.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.