O LevelFurther MathsCambridge (CIE)Additional MathsRevision NotesCalculusIntegrationIntegrating Powers of x

Integrating Powers of x (Cambridge (CIE) O Level Additional Maths): Revision Note

Exam code: 4037

Paul

Author

Paul

Last updated

Did this video help you?

Integrating Powers of x

How do I integrate powers of x?

  • Powers ofspace x are integrated according to the following formulae:

    • Ifspace f left parenthesis x right parenthesis equals x to the power of n thenspace integral f left parenthesis x right parenthesis space straight d x equals fraction numerator x to the power of n plus 1 end exponent over denominator n plus 1 end fraction plus c wherespace n element of straight rational numbers comma space n not equal to negative 1 andspace c is the constant of integration

    •  For each term …

      • … increase the power (of x) by 1

      • … divide by the new power

    • This does not apply when the original power is -1

      • the new power would be 0 and division by 0 is undefined

Formula for integrating x to the power of a constant

  • If the power ofspace x is multiplied by a constant then the integral is also multiplied by that constant

    • Ifspace f left parenthesis x right parenthesis equals a x to the power of n thenspace integral f left parenthesis x right parenthesis space straight d x equals fraction numerator a x to the power of n plus 1 end exponent over denominator n plus 1 end fraction plus c wherespace n element of straight rational numbers comma space n not equal to negative 1 andspace a is a constant andspace c is the constant of integration

  • Remember the special case:

    • space integral a space straight d x equals a x plus c

      • e.g. space integral 4 space straight d x equals 4 x plus c 

    • This allows constant terms to be integrated

How do I integrate expressions containing powers of x?

  • The formulae for integrating powers ofspace x apply to all rational numbers so it is possible to integrate any expression that is a sum or difference of powers ofspace x

    • e.g.  Ifspace f left parenthesis x right parenthesis equals 8 x cubed minus 2 x plus 4 thenspace integral f stretchy left parenthesis x stretchy right parenthesis blank straight d x equals fraction numerator 8 x to the power of 3 plus 1 end exponent over denominator 3 plus 1 end fraction minus fraction numerator 2 x to the power of 1 plus 1 end exponent over denominator 1 plus 1 end fraction plus 4 x plus c equals 2 x to the power of 4 minus x squared plus 4 x plus c

  • Functions involving roots will need to be rewritten as fractional powers ofspace x first

    • eg. Ifspace f left parenthesis x right parenthesis equals 5 cube root of x then rewrite asspace f left parenthesis x right parenthesis equals 5 x to the power of 1 third end exponent and integrate

  • Functions involving fractions with denominators in terms ofbold space bold italic x will need to be rewritten as negative powers ofspace x first

    • e.g.  Ifspace f left parenthesis x right parenthesis equals 4 over x squared plus x squared then rewrite asspace f left parenthesis x right parenthesis equals 4 x to the power of negative 2 end exponent plus x squared and integrate   

  • Products and quotients cannot be integrated this way so would need expanding/simplifying first

    • e.g.  Ifspace f stretchy left parenthesis x stretchy right parenthesis equals 8 x squared left parenthesis 2 x minus 3 right parenthesis thenError converting from MathML to accessible text.

Examiner Tips and Tricks

  • You can speed up the process of integration in the exam by committing the pattern of basic integration to memory

    • In general you can think of it as 'raising the power by one and dividing by the new power'

    • Practice this lots before your exam so that it comes quickly and naturally when doing more complicated integration questions

Worked Example

Given that

space fraction numerator straight d y over denominator straight d x end fraction equals 3 x to the power of 4 minus 2 x squared plus 3 minus fraction numerator 1 over denominator square root of x end fraction

find an expression forspace y in terms ofspace x.

Rewrite all terms as powers of x using the laws of indices for fractional and negative powers on the last term.

fraction numerator straight d y over denominator straight d x end fraction equals space 3 x to the power of 4 space minus space 2 x squared space plus space 3 space minus space x to the power of negative 1 half end exponent

Find y by integrating each term. 

y space equals space integral space open parentheses 3 x to the power of 4 space minus space 2 x squared space plus space 3 space minus space x to the power of negative 1 half end exponent space close parentheses space straight d x

y space equals fraction numerator space 3 x to the power of 5 over denominator 5 end fraction minus fraction numerator 2 x cubed over denominator 3 end fraction space plus space 3 x space minus fraction numerator space x to the power of 1 half end exponent over denominator 1 half end fraction space plus space c

Rewrite using the same format given in the question. 

bold italic y bold space bold equals bold space bold 3 over bold 5 bold italic x to the power of bold 5 bold space bold minus bold space bold 2 over bold 3 bold italic x to the power of bold 3 bold space bold plus bold space bold 3 bold italic x bold space bold minus bold space bold 2 square root of bold x bold space bold plus bold italic c

Did this video help you?

Finding the Constant of Integration

How do I find the constant of integration? 

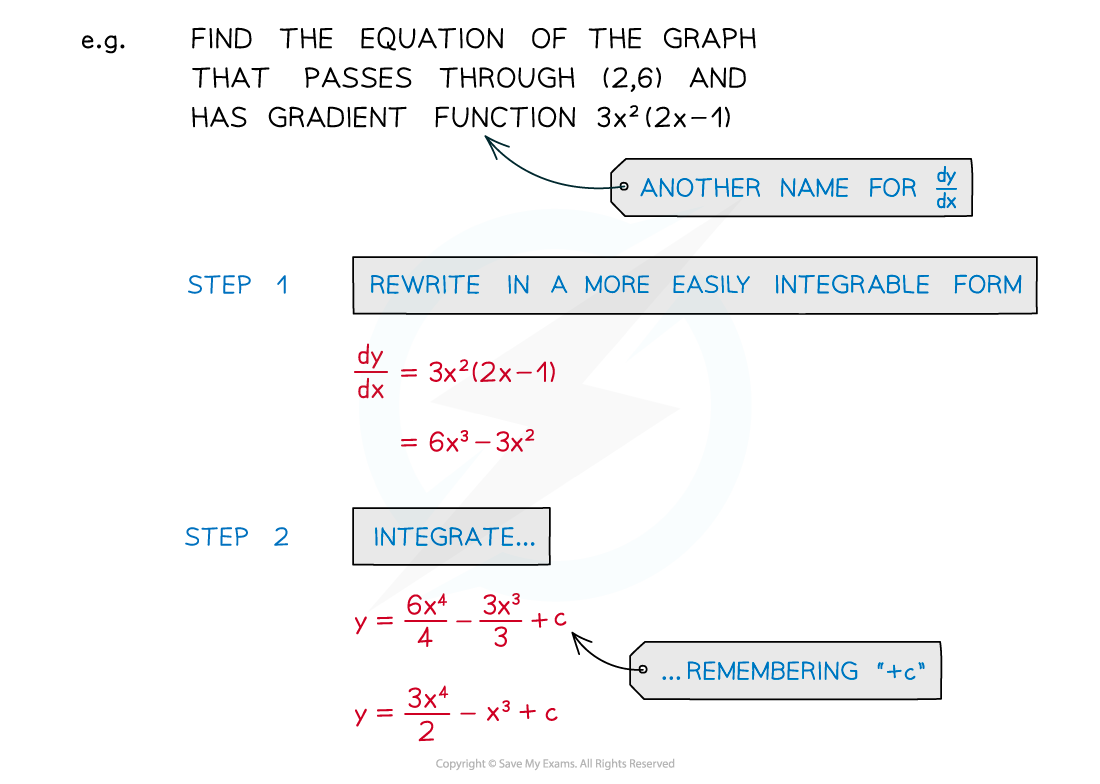
  • STEP 1 

    • Rewrite the function into a more easily integrable form

      • Each term needs to be a power of x (or a constant)

  • STEP 2 

    • Integrate each term and remember “+c”

      • Increase power by 1 and divide by new power

  • STEP 3

    • Substitute the coordinates of a given point in to form an equation in c

      • Solve the equation to find c

Notes fig3, A Level & AS Level Pure Maths Revision Notes

 

Example of finding the constant of integration

 

Examiner Tips and Tricks

  • If a constant of integration can be found then the question will need to give you some extra information

    • If this is given then make sure you use it to find the value of c

Worked Example

Given straight f apostrophe open parentheses x close parentheses space equals space fraction numerator open parentheses x plus 3 close parentheses squared over denominator square root of x end fraction and straight f open parentheses 1 close parentheses space equals space 25, find straight f open parentheses x close parentheses.   

Rewrite straight f to the power of apostrophe open parentheses x close parentheses in a form the can be integrated more easily. 

table row cell straight f to the power of apostrophe open parentheses x close parentheses space end cell equals cell space fraction numerator open parentheses x plus 3 close parentheses open parentheses x plus 3 close parentheses over denominator square root of x end fraction end cell row blank equals cell space fraction numerator x to the power of 2 space end exponent plus space 6 x space plus space 9 over denominator x to the power of 1 half end exponent end fraction end cell row space equals cell fraction numerator space x squared over denominator x to the power of 1 half end exponent end fraction space plus fraction numerator space 6 x over denominator x to the power of 1 half end exponent end fraction space plus fraction numerator space 9 over denominator x to the power of 1 half end exponent end fraction end cell row blank equals cell space x to the power of 3 over 2 space end exponent plus space 6 x to the power of 1 half end exponent space plus space 9 x to the power of negative 1 half end exponent end cell end table   

Integrate each term, remember to include a constant of integration.

straight f open parentheses x close parentheses space equals fraction numerator space x to the power of 5 over 2 end exponent over denominator 5 over 2 end fraction plus fraction numerator 6 x to the power of 3 over 2 end exponent over denominator 3 over 2 end fraction plus fraction numerator 9 x to the power of 1 half end exponent over denominator 1 half end fraction plus c   

Simplify.

straight f open parentheses x close parentheses space equals 2 over 5 x to the power of 5 over 2 end exponent plus 4 x to the power of 3 over 2 end exponent plus 18 x to the power of 1 half end exponent plus c

Use f(1) =25 to find the value of c.

straight f open parentheses 1 close parentheses space equals 2 over 5 open parentheses 1 close parentheses to the power of 5 over 2 end exponent plus 4 open parentheses 1 close parentheses to the power of 3 over 2 end exponent plus 18 open parentheses 1 close parentheses to the power of 1 half end exponent plus c

table row cell 2 over 5 plus 4 plus 18 space plus c space end cell equals cell space 25 end cell row cell 22 2 over 5 space plus space c space end cell equals cell space 25 end cell row cell c space end cell equals cell fraction numerator space 13 space over denominator 5 end fraction end cell end table

bold f stretchy left parenthesis x stretchy right parenthesis bold space bold equals bold 2 over bold 5 bold italic x to the power of bold 5 over bold 2 end exponent bold space bold plus bold space bold 4 bold italic x to the power of bold 3 over bold 2 end exponent bold space bold plus bold space bold 18 bold italic x to the power of bold 1 over bold 2 end exponent bold space bold plus fraction numerator bold space bold 13 over denominator bold 5 end fraction

👀 You've read 1 of your 5 free revision notes this week
An illustration of students holding their exam resultsUnlock more revision notes. It's free!

By signing up you agree to our Terms and Privacy Policy.

Already have an account? Log in

Test yourself

Did this page help you?

Previous:Introduction to IntegrationNext:Definite Integrals
Paul

Author: Paul

Expertise: Maths Content Creator

Paul has taught mathematics for 20 years and has been an examiner for Edexcel for over a decade. GCSE, A level, pure, mechanics, statistics, discrete – if it’s in a Maths exam, Paul will know about it. Paul is a passionate fan of clear and colourful notes with fascinating diagrams.

Download notes on Integrating Powers of x