AP®PhysicsCollege BoardPhysics 1: Algebra-BasedStudy GuidesUnit 5: Torque & Rotational DynamicsRotational InertiaRotational Inertia

Rotational Inertia (College Board AP® Physics 1: Algebra-Based): Study Guide

Katie M

Written by: Katie M

Reviewed by: Caroline Carroll

Updated on

Rotational inertia

  • In linear motion, the resistance to a change of motion, i.e. linear acceleration, is known as inertia

    • The more mass an object has, the greater its inertia

  • When a rigid system has rotational motion relative to a specified axis of rotation, its distribution of mass around that axis must be considered

    • This is described by its rotational inertia

  • The rotational inertia of a rigid system is defined as:

The resistance to a change of rotational motion, depending on the system's distribution of mass around a chosen axis of rotation

  • Rotational inertia is measured in kg times straight m squared

  • The rotational inertia of a body depends on many factors, such as:

    • its shape

    • its density

    • its orientation (relative to an axis of rotation)

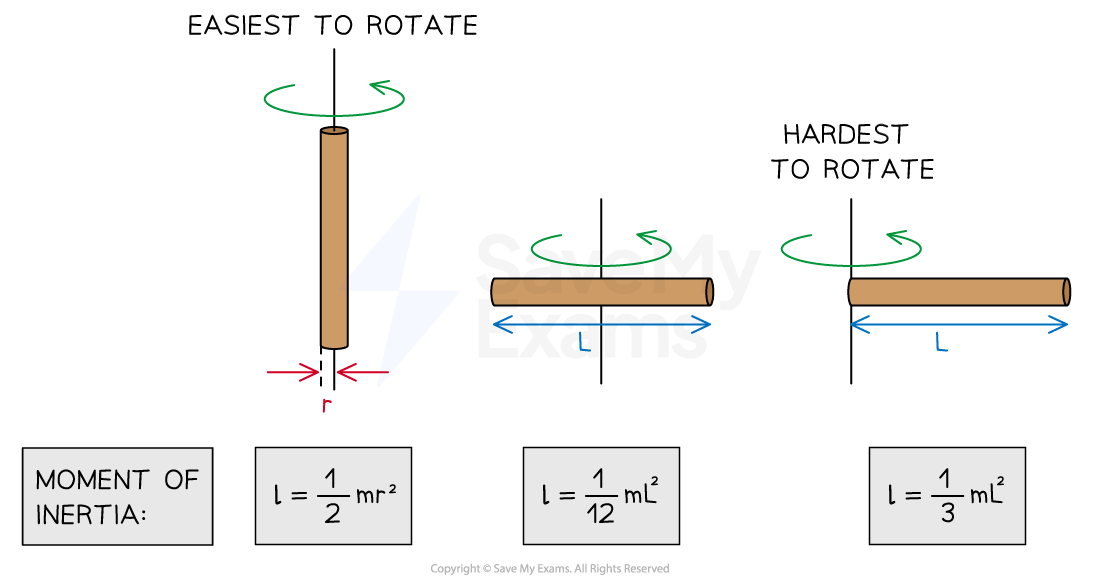
  • For example, the rotational inertia of a thin rod is different for each of the following orientations:

    • Rotation about its vertical axis

    • Rotation about its center of mass

    • Rotation about one end

Diagram showing the difference in rotational inertia for a thin rod about different axes of rotation. Formulas: I = (1/2)mr², I = (1/12)mL², I = (1/3)mL².
The rotational inertia of a body can change depending on its orientation relative to the axis of rotation. The more rotational inertia an object has, the harder it is to rotate

Examiner Tips and Tricks

Make sure you are clear on the distinction between linear motion and rotational motion here. The implications of considering the distribution of masses in relation to an axis of rotation, as opposed to considering them as uniform, have important consequences when carrying out calculations in rotational dynamics

Rotational inertia equation

  • The rotational inertia of an object is equal to:

I space equals space m r squared

  • Where:

    • I = rotational inertia, in kg times straight m squared

    • m = mass of the object, in kg

    • r = perpendicular distance from an axis of rotation, in straight m

  • This equation applies to objects which can be considered as a point mass

Total rotational inertia of a system

  • The total rotational inertia of a system about an axis is equal to the sum of the rotational inertias of each object about that axis:

I subscript t o t end subscript space equals space sum for i of I subscript i space equals space sum for i of m subscript i r subscript i superscript 2

  • The rotational inertias of some common extended, rigid bodies are shown below:

Rotational inertia of extended rigid systems

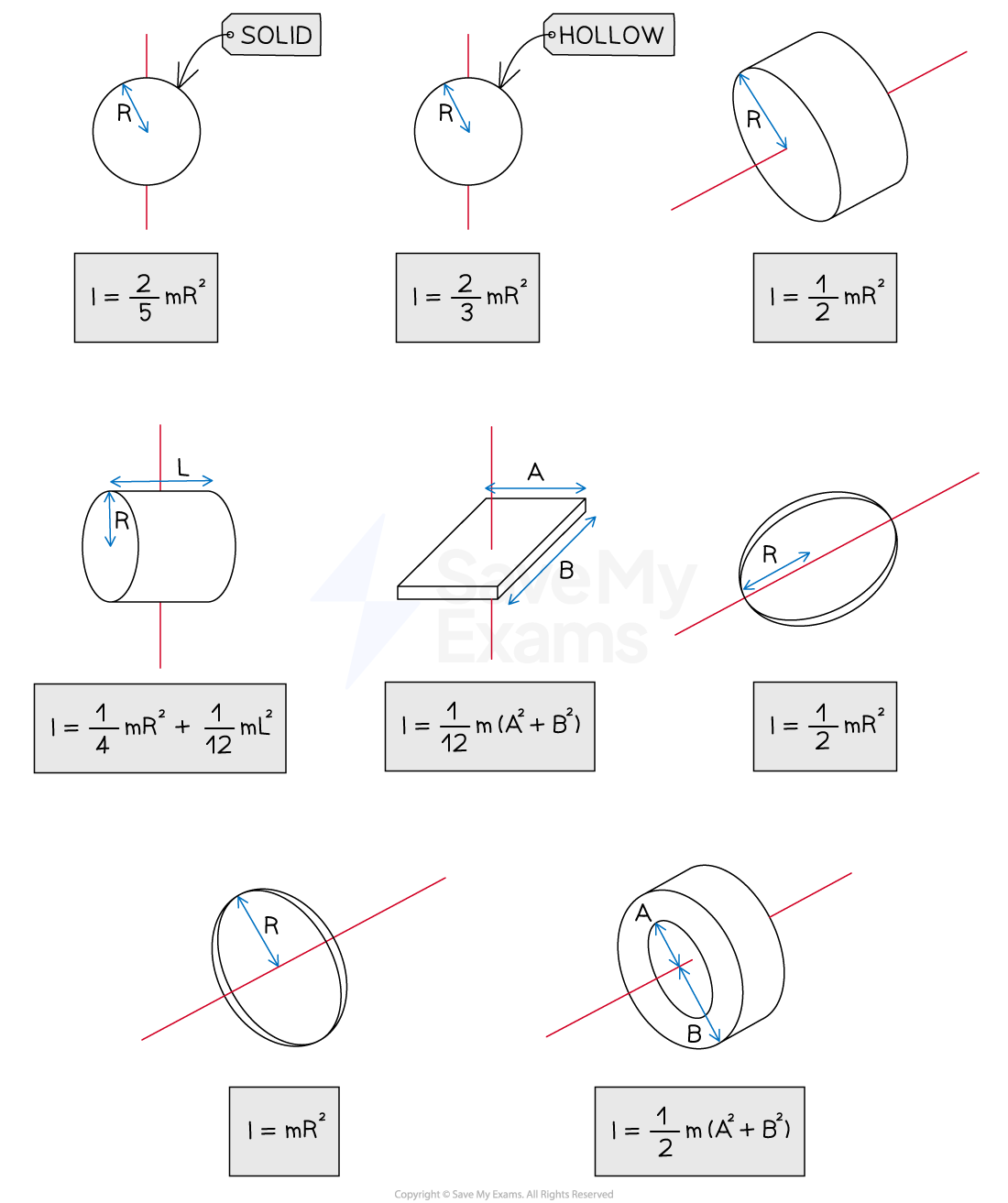
Diagrams showing moments of inertia for various objects: solid and hollow spheres, cylindrical shells, bars through different axes, and solid and hollow cylinders, each with formulas.
Rotational inertia of common extended rigid bodies, where R represents radius and L represents length, as shown

  • Extended rigid bodies may have the same shape but different rotational inertia

  • For example, a hollow cylinder and a solid cylinder of the same mass and radius have different rotational inertia

    • The hollow cylinder has more rotational inertia as its mass is distributed further from the axis of rotation

    • The solid cylinder has less rotational inertia as its mass is distributed closer to the axis of rotation

Worked Example

A rigid system comprises a vertical support post and two horizontal rods of negligible mass. Two objects of mass m are attached to the ends of the upper horizontal rod of length 2 r, and two objects of mass 2 m are attached to the ends of the lower horizontal rod of length 4 r.

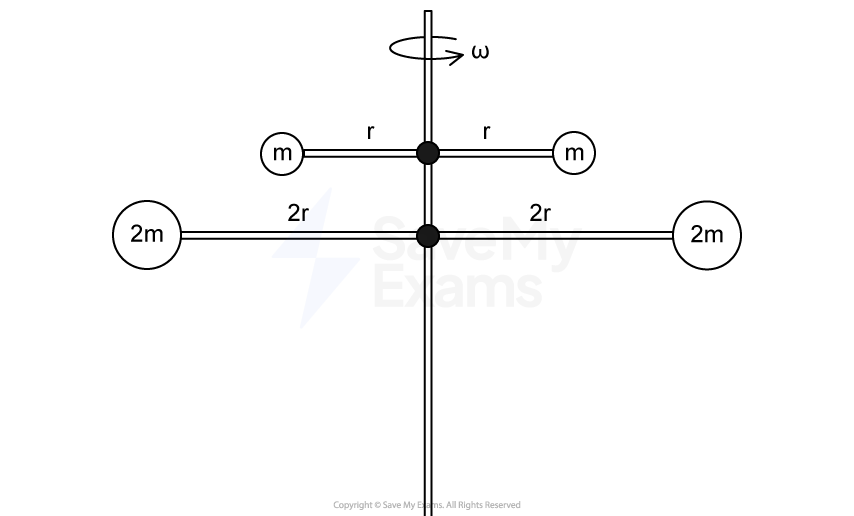
Diagram of a rotating system with four masses connected by rods. Two arms of length L with mass m at ends, and two perpendicular arms of length 2L with mass 2m at ends.

(A) Calculate the total rotational inertia of the rigid system.

(B) Do the two upper objects make a greater, lesser, or equal contribution to the total rotational inertia of the system than the two lower objects?

Answer:

Part (A)

Step 1: Analyze the scenario

  • The total rotational inertia of the rigid system is the sum of

    • the rotational inertia of two upper objects about the vertical rod

    • the rotational inertia of the two lower objects about the vertical rod

Step 2: Calculate the rotational inertia of the upper objects

  • The mass of each object is m

  • The distance between the rotational axis and each object is r

I subscript u p p e r end subscript space equals space sum m r squared

I subscript u p p e r end subscript space equals space m r squared space plus space m r squared space equals space 2 m r squared

Step 3: Calculate the rotational inertia of the lower objects

  • The mass of each object is 2 m

  • The distance between the rotational axis and each object is 2 r

I subscript l o w e r end subscript space equals space sum m r squared

I subscript l o w e r end subscript space equals space 2 m open parentheses 2 r close parentheses squared space plus space 2 m open parentheses 2 r close parentheses squared space equals space 16 m r squared

Step 4: Calculate the total rotational inertia of the system

I subscript t o t end subscript space equals space I subscript u p p e r end subscript space plus space I subscript l o w e r end subscript

I subscript t o t end subscript space equals space 2 m r squared italic space plus space 16 m r squared space equals space 18 m r squared

Part (B)

Step 1: Analyze the scenario

  • The proportion of rotational inertia contributed by the two upper objects is given by:

I subscript u p p e r end subscript over I subscript t o t end subscript space equals space fraction numerator 2 m r squared over denominator 18 m r squared end fraction space equals space 0.11 space almost equal to space 11 percent sign

  • The proportion of rotational inertia contributed by the two lower objects is given by:

I subscript l o w e r end subscript over I subscript t o t end subscript space equals space fraction numerator 16 m r squared over denominator 18 m r squared end fraction space equals space 0.89 space almost equal to space 89 percent sign

Step 2: Compare the contribution of the rotational inertias

  • The two upper objects make a lesser contribution to the total rotational inertia of the system than the two lower objects

Examiner Tips and Tricks

For the AP Physics 1 exam, you will only be expected to calculate the rotational inertia for systems of five or fewer objects arranged in a two-dimensional configuration.

You will never be expected to memorize the rotational inertia of different extended rigid systems as they will always be given in an exam question where required.

👀 You've read 1 of your 5 free study guides this week
An illustration of students holding their exam resultsUnlock more study guides. It's free!

By signing up you agree to our Terms and Privacy Policy.

Already have an account? Log in

Test yourself

Did this page help you?

Previous:Force Diagrams & TorqueNext:Parallel Axis Theorem
Author
Reviewer
Katie M

Author: Katie M

Expertise: Physics Content Creator

Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.

Caroline Carroll

Reviewer: Caroline Carroll

Expertise: Physics & Chemistry Subject Lead

Caroline graduated from the University of Nottingham with a degree in Chemistry and Molecular Physics. She spent several years working as an Industrial Chemist in the automotive industry before retraining to teach. Caroline has over 12 years of experience teaching GCSE and A-level chemistry and physics. She is passionate about creating high-quality resources to help students achieve their full potential.

Download notes on Rotational Inertia