IGCSEMathsEdexcelMaths AFoundationRevision Notes4. Geometry & TrigonometryVolume & Surface AreaVolume

Volume (Edexcel IGCSE Maths A): Revision Note

Exam code: 4MA1

Naomi C

Author

Naomi C

Last updated

Did this video help you?

Volume

What is volume?

  • The volume of a 3D shape is a measure of how much space it takes up

  • You need to be able to calculate the volumes of a number of common 3D shapes, including:

    • Cubes and cuboids

    • Prisms

    • Pyramids

    • Cylinders

    • Spheres

How do I find the volume of a cube or a cuboid?

  • A cube is a special cuboid, where the length, width and height are all of equal length

  • A cuboid is another name for a rectangular-based prism

  • To find the volume, V, of a cube or a cuboid, with length, l, width, w, and height, h, use the formula

    • V equals l w h

    • This formula is not given to you in the exam

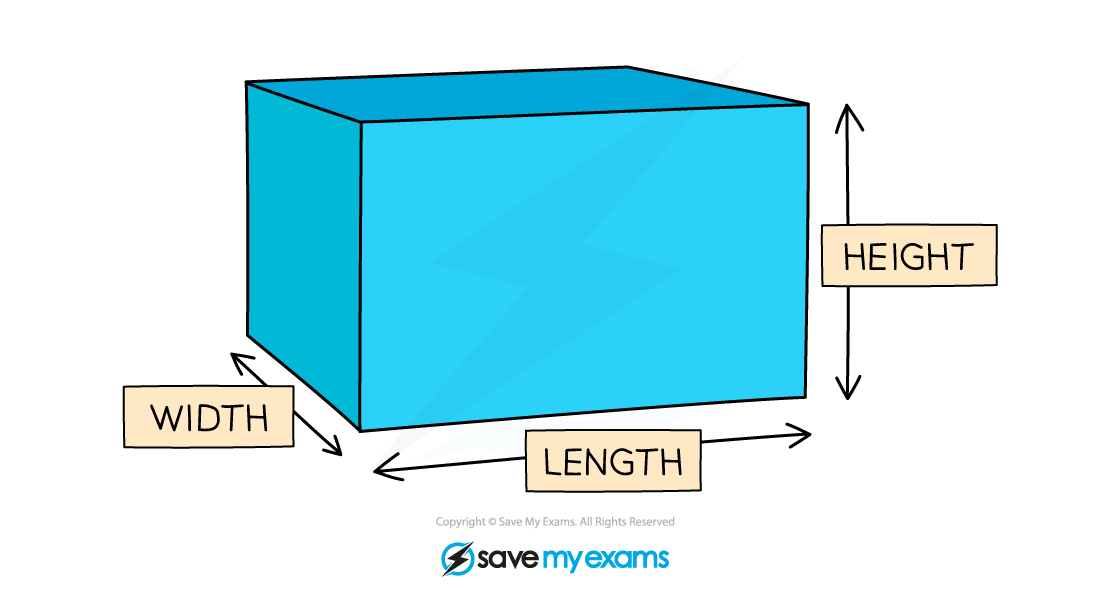
Volume of a cuboid

  • You will sometimes see the terms  'depth' or 'breadth' instead of 'height' or 'width'

How do I find the volume of a prism?

  • A prism is a 3D object with a constant cross-sectional area

  • To find the volume, V, of a prism, with cross-sectional area, A, and length, l, use the formula

    • V equals A l

    • This formula is not given to you in the exam

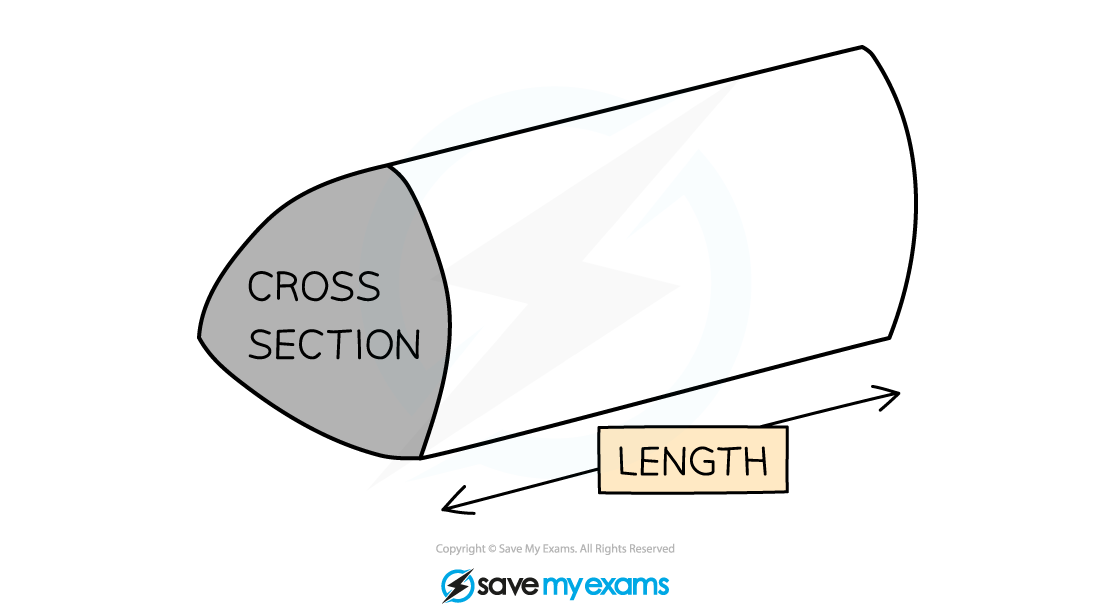
Volume of a prism

  • Note that the cross-section can be any shape, so as long as you know its area and the length of the prism, you can calculate its volume

    • If you know the volume and length of the prism, you can calculate the area of the cross-section

How do I find the volume of a cylinder?

  • To calculate the volume, V, of a cylinder with radius, r, and height, h, use the formula

    • V equals pi italic space r squared h

    • This formula is not given to you in the exam

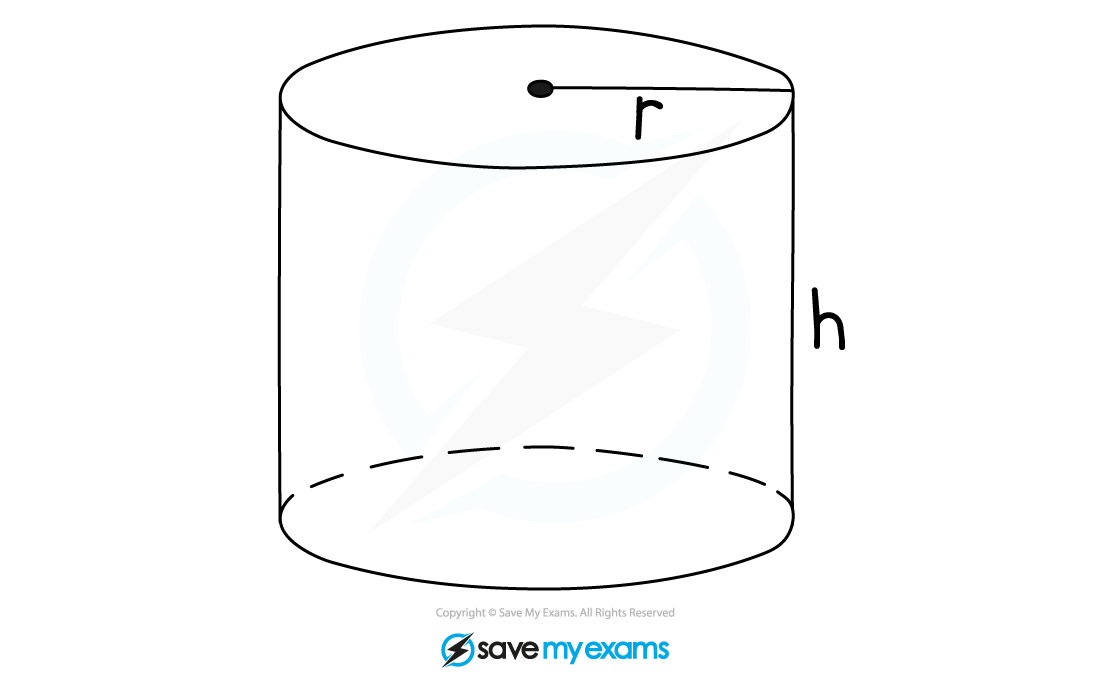
Volume of a cylinder

  • Note that a cylinder is similar to a prism, its cross-section is a circle with area pi italic space r squared, and its length is h

How do I find the volume of a pyramid?

  • To calculate the volume, V, of a pyramid with base area, A, and perpendicular height, h, use the formula

    • V equals 1 third A h

    • This formula is given to you in the exam

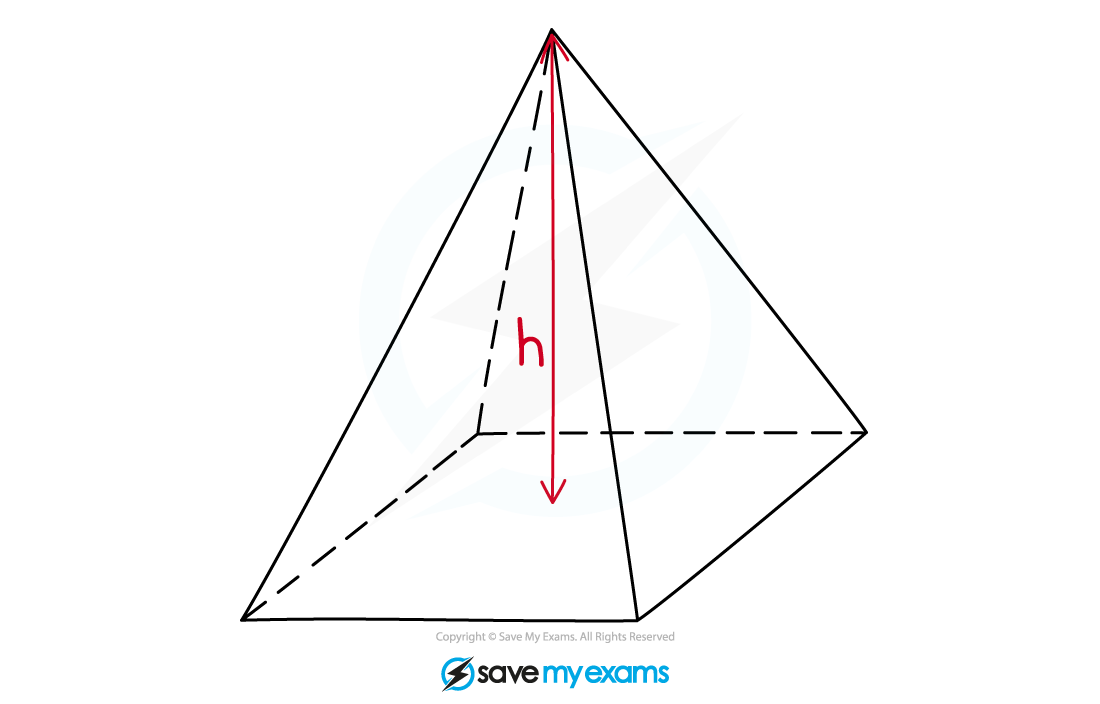
Volume of a pyramid

  • The height must be a line from the top of the pyramid that is perpendicular to the base

  • The base of a pyramid could be a square, a rectangle or a triangle

How do I find the volume of a cone?

  • To calculate the volume, V, of a cone with base radius, r, and perpendicular height, h, use the formula

    • V equals 1 third pi italic space r to the power of italic 2 h

    • This formula is given to you in the exam

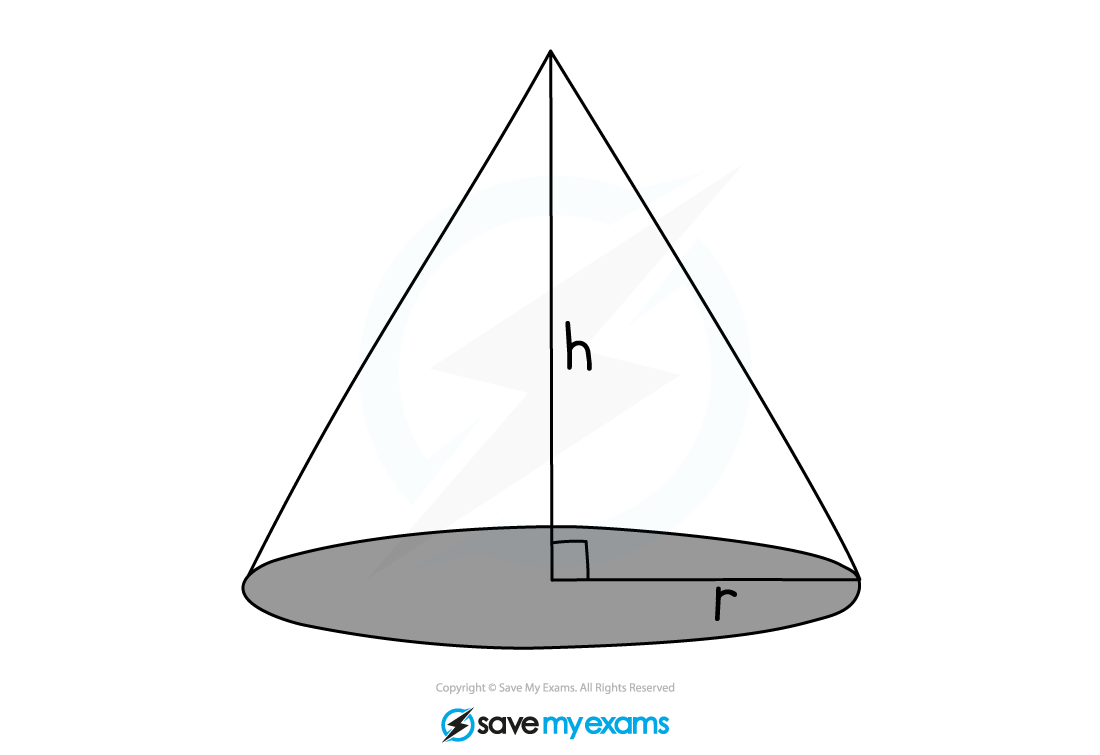
Cone volume, IGCSE & GCSE Maths revision notes

  • Note that volume formula for a cone is similar to a pyramid

  • The height must be a line from the top of the cone that is perpendicular to the base

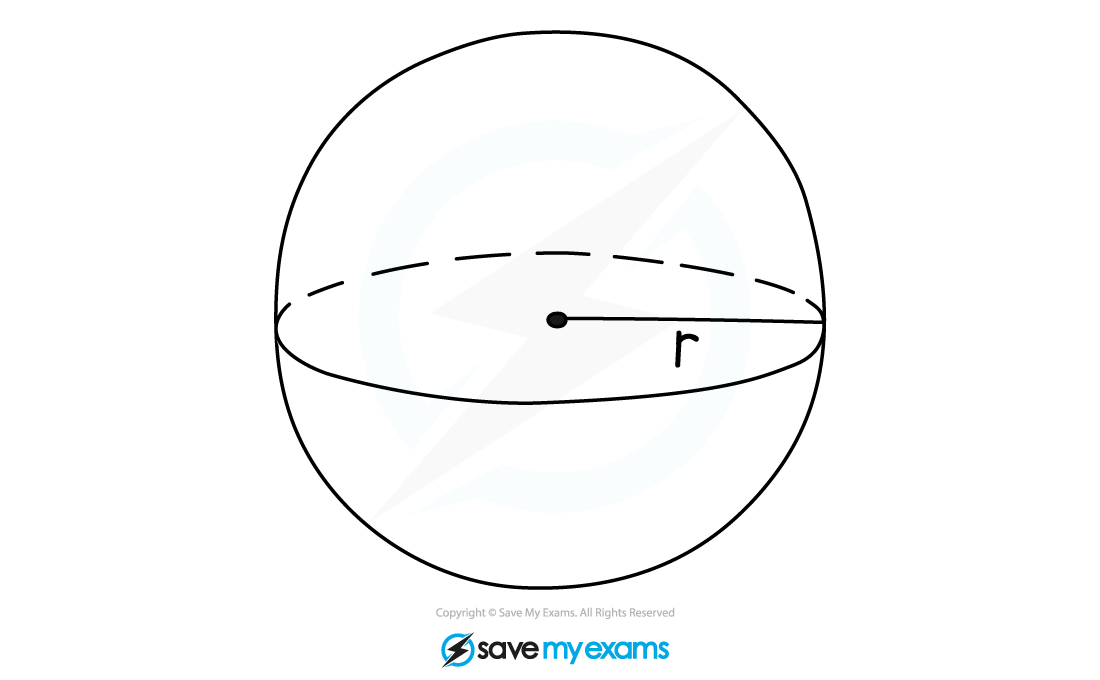
How do I find the volume of a sphere?

  • To calculate the volume, V, of a sphere with radius, r, use the formula

    • V equals 4 over 3 pi italic space r cubed

    • This formula is given to you in the exam

Sphere Radius r, IGCSE & GCSE Maths revision notes

Examiner Tips and Tricks

  • You only need to memorise the volume formulae for:

    • Cuboids: V equals l w h

    • Prisms: V equals A l

    • Cylinders: V equals pi italic space r squared h

Worked Example

A cylinder is shown.

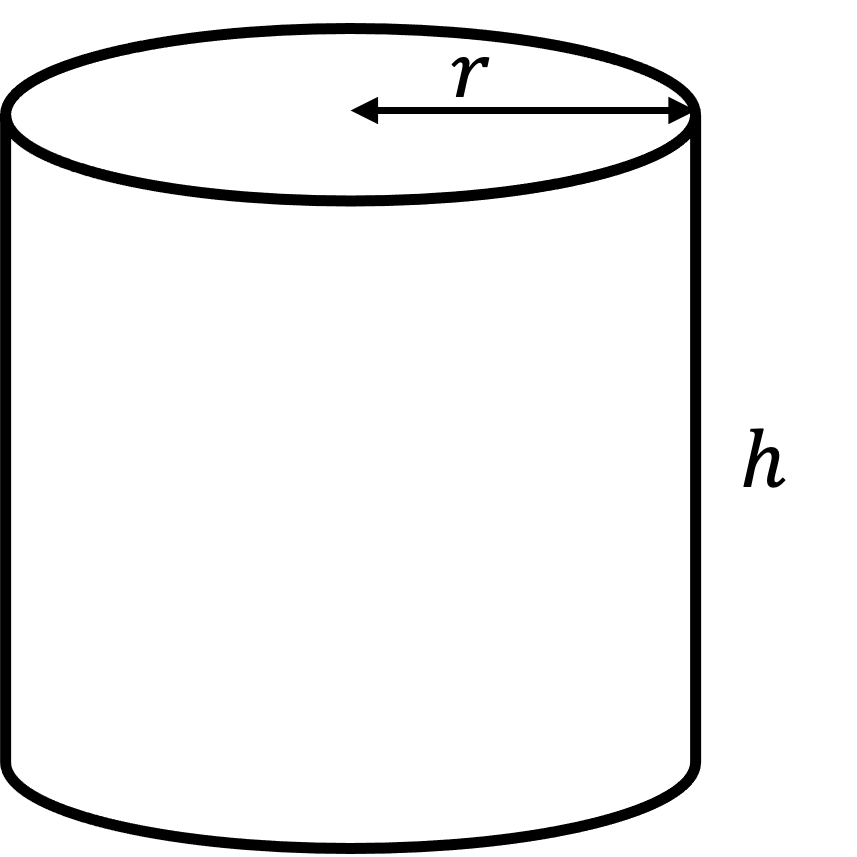
Cylinder

The radius, r, is 8 cm and the height, h, is 20 cm.

Calculate the volume of the cylinder, giving your answer correct to 3 significant figures.
 

A cylinder is similar to a prism but with a circular base
The volume of any prism, V, is its base area × height, h, where the base area here is for a circle, pi italic space r squared
 

V equals pi space r squared h
 

Substitute r  = 8 and h  = 20 into the formula
 

V equals straight pi cross times 8 squared cross times 20
 

Work out this value on a calculator
 

4021.238...
 

Round the answer to 3 significant figures

4020 cm3

You've read 1 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

  • I would just like to say a massive thank you for putting together such a brilliant, easy to use website.I really think using this site helped me secure my top gradesin science and maths. You really did save my exams! Thank you.

    Beth
    IGCSE Student

  • This website is soooo useful and I can’t ever thank you enough for organising questions by topic like this. Furthermore, the name of the website could not have been more appropriate as it literally did SAVE MY EXAMS!

    Fathima
    A Level Student

Did this page help you?

Previous:Arc Lengths & Sector AreasNext:Problem Solving with Volumes
Naomi C

Author: Naomi C

Expertise: Maths Content Creator

Naomi graduated from Durham University in 2007 with a Masters degree in Civil Engineering. She has taught Mathematics in the UK, Malaysia and Switzerland covering GCSE, IGCSE, A-Level and IB. She particularly enjoys applying Mathematics to real life and endeavours to bring creativity to the content she creates.

Download notes on Volume