Centripetal Acceleration (Edexcel International A Level (IAL) Physics): Revision Note
Exam code: YPH11
Deriving Equations for Centripetal Acceleration
An object moving in uniform circular motion travels with a constant angular velocity and angular speed
However, its direction is always changing
Therefore, its linear velocity changes, so it must be accelerating
This is called a centripetal acceleration
An object in circular motion is thus always accelerating
This acceleration is called 'centripetal' because it is directed toward the centre of orbit
To derive an equation for the magnitude of centripetal acceleration, consider an object in uniform circular motion between point A and B on a circle, as shown below:
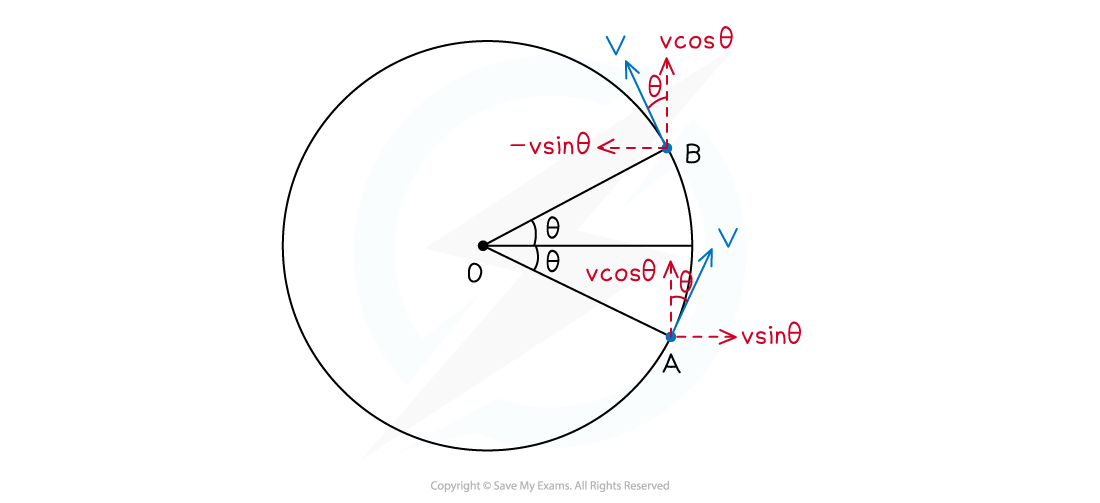
An object in uniform circular motion is accelerating toward the centre of orbit, O. Between A and B, the horizontal component of motion changes from v sinθ to –v sinθ
At A and B, by resolving the horizontal and vertical components of linear velocity v, it can be seen that:
Initial vertical component of v = final vertical component of v which is v cosθ
Initial horizontal component of v is v sinθ
Final horizontal component of v is –v sinθ
This means the acceleration of the object is only horizontal, given by:
Recalling the equations for angular velocity ω = θ /t and v = rω, then:
The object's angular displacement is actually 2θ, therefore, the time t is given by
Therefore, substituting this into the equation for acceleration gives:
This equation is the acceleration of the object between points A and B
To find the instantaneous acceleration at an exact point on the circle, say point C, reduce the size of the angular displacement θ so it becomes infinitesimally small
This is shown in the image below:

By taking the limit of angular displacement as zero, we can derive an equation for the instantaneous centripetal acceleration of the object at point C
In the limit θ → 0 radians
The value of sin θ is approximately equal to θ
Therefore,
(for very small angles)
This is known as the small angle approximation
Therefore, the instantaneous acceleration is the centripetal acceleration:
Where:
a = centripetal acceleration (m s–2)
v = linear velocity (m s–1)
r = radius of orbit (m)
ω = angular velocity (rad s-1)
The negative sign indicates that the centripetal acceleration is directed toward the centre of orbit
Examiner Tips and Tricks
This seems like a complicated derivation, but there is no maths in there that you haven't been introduced to already. It is important you know how to use the vector diagrams to reach the final equations for angular accelerations, understanding every step along the way. Try and do it without the notes to help memorise and see how far you get!
Using Equations for Centripetal Acceleration
Centripetal acceleration is defined as:
The acceleration of an object towards the centre of a circle when an object is in motion (rotating) around a circle at a constant speed
Its magnitude is calculated using the radius r and linear speed v:
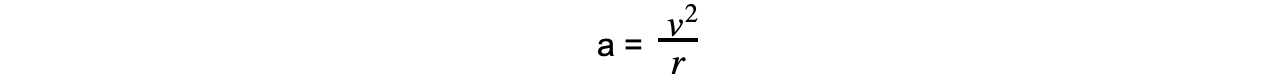
Using the equation relating angular speed ω and linear speed v:
v = r⍵
These equations can be combined to give another form of the centripetal acceleration equation:

This equation shows that centripetal acceleration is equal to the radius times the square of the angular speed
Alternatively, rearrange for r:
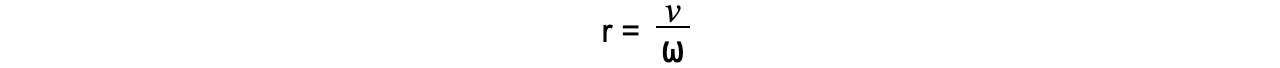
This equation can be combined with the first one to give us another form of the centripetal acceleration equation:
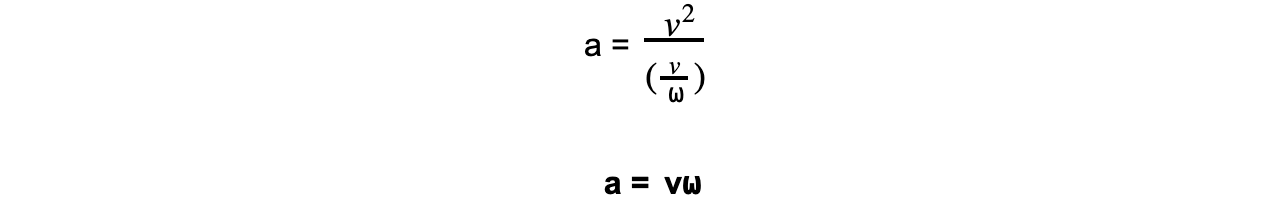
This equation shows how the centripetal acceleration relates to the linear speed and the angular speed
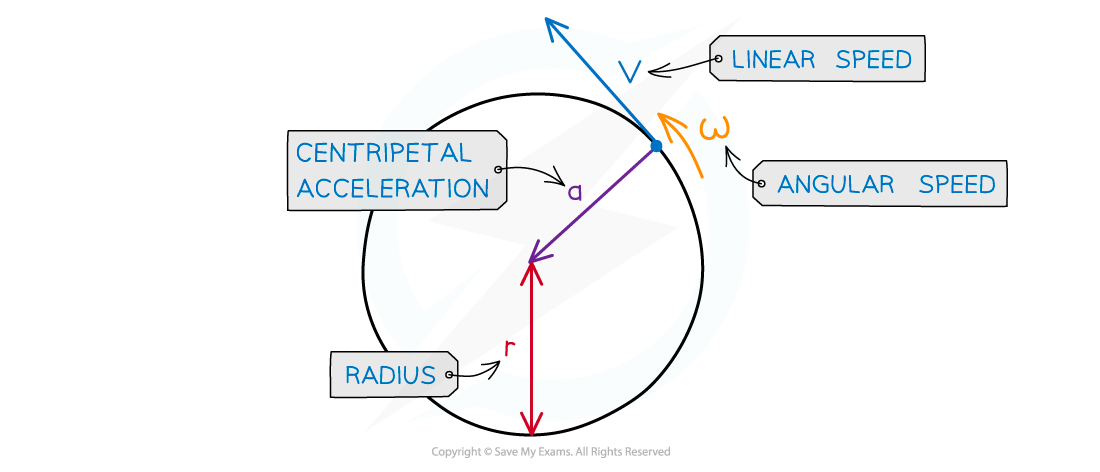
Centripetal acceleration is always directed toward the centre of the circle, and is perpendicular to the object’s velocity
Where:
a = centripetal acceleration (m s−2)
v = linear speed (m s−1)
⍵ = angular speed (rad s−1)
r = radius of the orbit (m)
Worked Example
A ball tied to a string is rotating in a horizontal circle with a radius of 1.5 m and an angular speed of 3.5 rad s−1.
Calculate its centripetal acceleration if the radius was twice as large and angular speed was twice as fast.
Answer:

Examiner Tips and Tricks
Make sure you understand both the derivation and how to use the equation for centripetal acceleration. The most crucial step is to remember the small angle approximation, that sin θ is approximately equal to θ when the angle is very very small. Try this in your calculator (in radians!) and see for yourself!

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?