Average Molecular Kinetic Energy (Edexcel International A Level (IAL) Physics): Revision Note
Exam code: YPH11
Average Molecular Kinetic Energy
An important property of molecules in a gas is their average kinetic energy
This can be deduced from the ideal gas equations relating pressure, volume, temperature and speed
Recall the ideal gas equation in terms of number of molecules:
pV = NkT
Also, recall the equation linking pressure and mean square speed of the molecules:
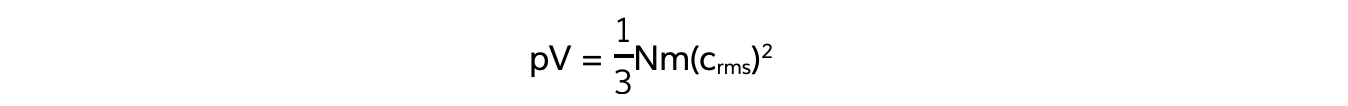
The left-hand side of both equations are equal to pV
This means the right-hand sides of both equations are also equal:
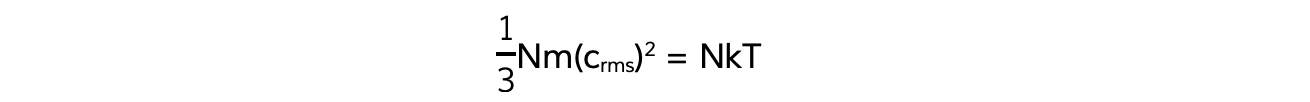
N will cancel out on both sides and multiplying by 3 on both sides too obtains the equation:
m(crms)2 = 3kT
Recall the familiar kinetic energy equation from mechanics:

Instead of v2 for the velocity of one particle, (crms)2 is the average speed of all molecules
Multiplying both sides of the equation by ½ obtains the average molecular kinetic energy of the molecules of an ideal gas:
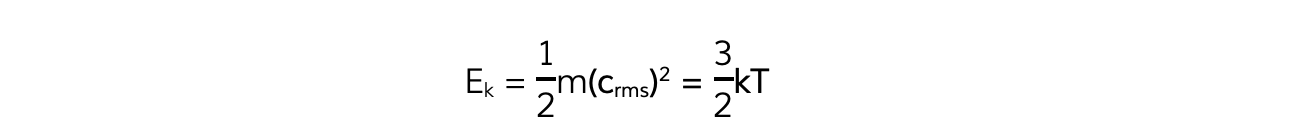
Where:
Ek = kinetic energy of a molecule (J)
m = mass of one molecule (kg)
(crms)2 = mean square speed of a molecule (m2 s-2)
k = Boltzmann constant
T = temperature of the gas (K)
Note: this is the average kinetic energy for only one molecule of the gas
To find the average kinetic energy for many molecules of the gas, multiply both sides of the equation by the number of molecules N to obtain:
Ek = Nm(c)2 =
NkT
A key feature of this equation is that the mean kinetic energy of an ideal gas molecule is proportional to its thermodynamic temperature
Ek ∝ T
The Boltzmann constant k can be replaced with
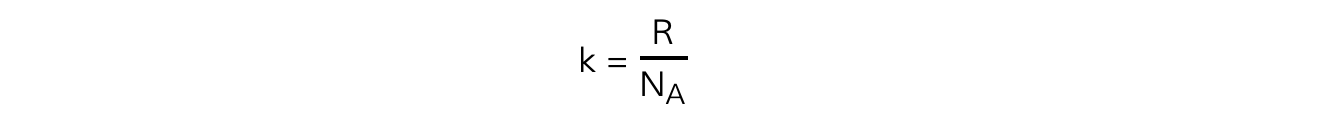
Substituting this into the average molecular kinetic energy equation means it can also be written as:

Worked Example
Helium can be treated as an ideal gas. Helium molecules have a root-mean-square (r.m.s.) speed of 720 m s-1 at a temperature of 45 °C. Calculate the r.m.s. speed of the molecules at a temperature of 80 °C.
Answer:

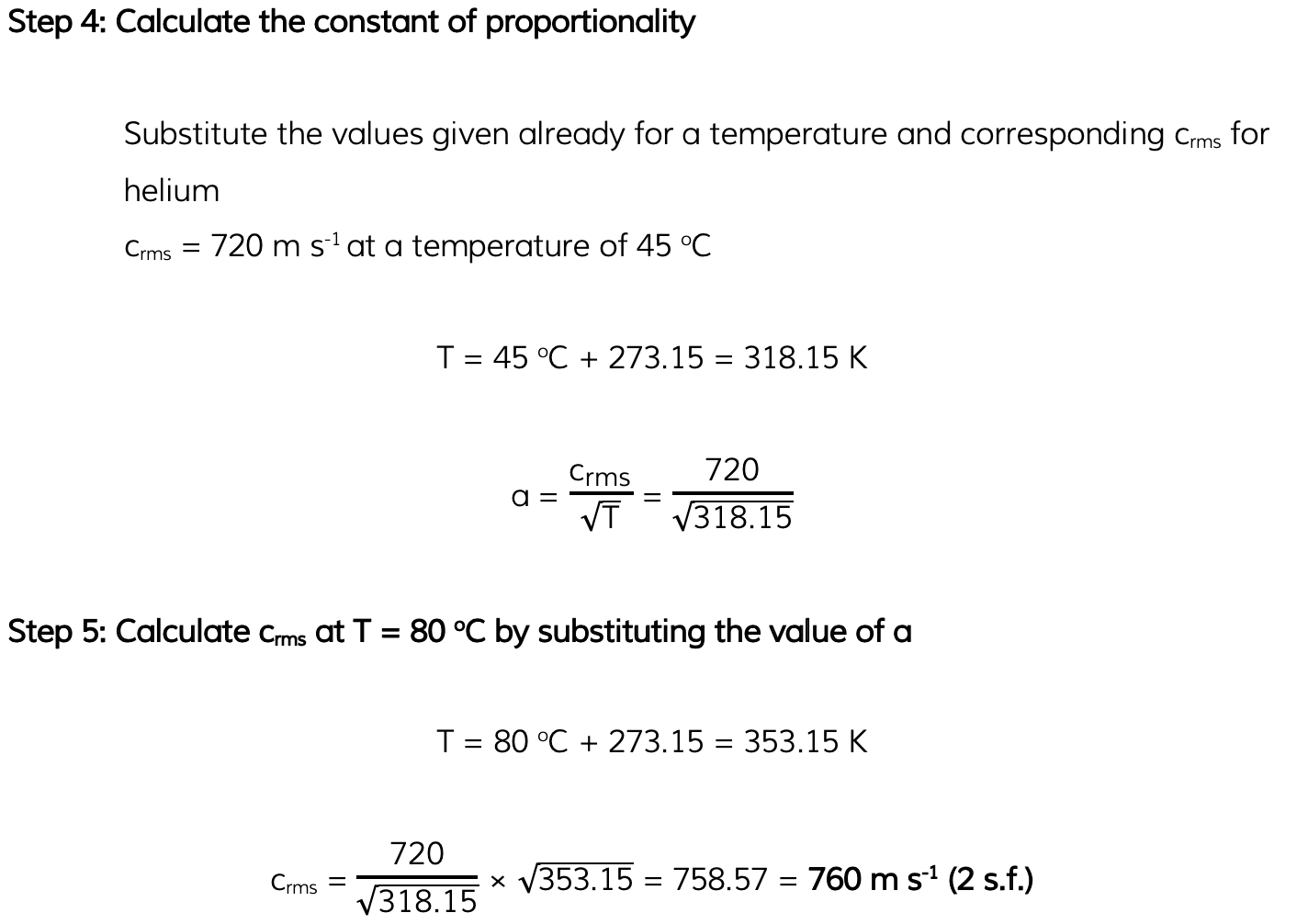
Examiner Tips and Tricks
You can remember the equation through the rhyme ‘Average K.E is three-halves kT’.

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?