Nuclear Binding Energy & Mass Deficit (Edexcel International A Level (IAL) Physics): Revision Note
Exam code: YPH11
Nuclear Binding Energy
Experiments into nuclear structure have found that the total mass of a nucleus is less than the sum of the masses of its constituent nucleons
This difference in mass is known as the mass defect or mass deficit
Mass defect is defined as:
The difference between the measured mass of a nucleus and the sum total of the masses of its constituents
The mass defect Δm of a nucleus can be calculated using:
Where:
Z = proton number
A = nucleon number
mp = mass of a proton (kg)
mn = mass of a neutron (kg)
mtotal = measured mass of the nucleus (kg)
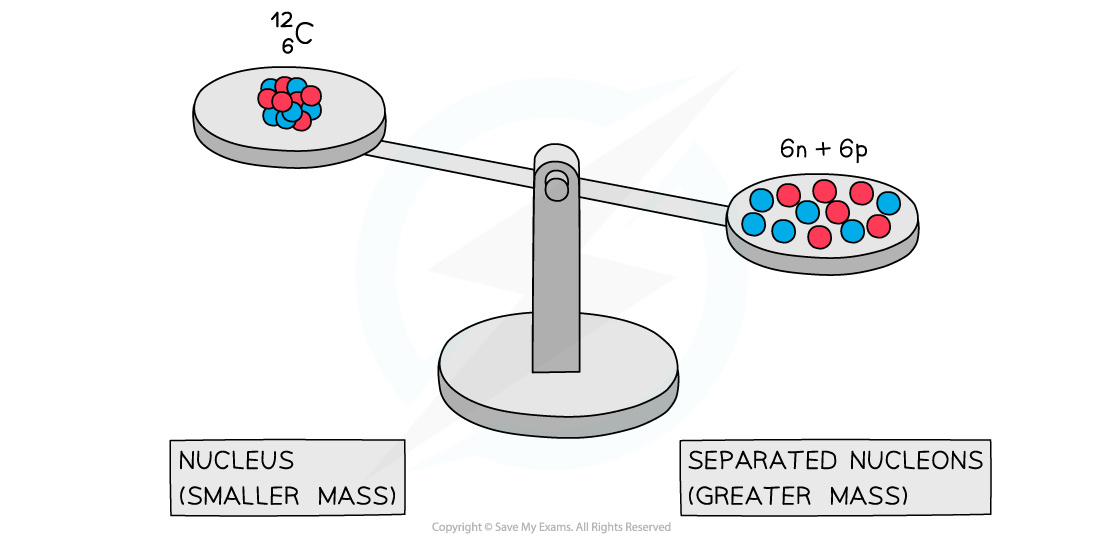
A system of separated nucleons has a greater mass than a system of bound nucleons
Due to mass-energy equivalence, this decrease in mass implies that energy is released
Energy and mass are proportional, so, the total energy of a nucleus is less than the sum of the energies of its constituent nucleons
Binding energy is defined as:
The energy required to break a nucleus into its constituent protons and neutrons
The formation of a nucleus from a system of isolated protons and neutrons therefore releases energy, making it an exothermic reaction
This can be calculated using the equation:
Mass-Energy Equivalence
Einstein showed in his Theory of Relativity that matter can be considered a form of energy and hence, he proposed:
Mass can be converted into energy
Energy can be converted into mass
This is known as mass-energy equivalence, and can be summarised by the equation:
Where:
E = energy (J)
m = mass (kg)
c = the speed of light (m s-1)
Some examples of mass-energy equivalence are:
The fusion of hydrogen into helium in the centre of the sun
The fission of uranium in nuclear power plants
Nuclear weapons
High-energy particle collisions in particle accelerators
Worked Example
The binding energy per nucleon is 7.98 MeV for an atom of Oxygen-16 (16O).
Determine an approximate value for the energy required, in MeV, to completely separate the nucleons of this atom.
Answer:
Step 1: List the known quantities
Binding energy per nucleon, E = 7.98 MeV
Step 2: State the number of nucleons
The number of nucleons is 8 protons and 8 neutrons, therefore 16 nucleons in total
Step 3: Find the total binding energy
The binding energy for oxygen-16 is:
7.98 × 16 = 127.7 MeV
Step 4: State the final answer
The approximate total energy needed to completely separate this nucleus is 127.7 MeV
Examiner Tips and Tricks
Binding energy is named in a confusing way, so be careful!
Avoid describing the binding energy as the energy stored in the nucleus – this is not correct – it is energy that must be put into the nucleus to pull it apart.

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?