Equations for Simple Harmonic Motion (Edexcel International A Level (IAL) Physics): Revision Note
Exam code: YPH11
Equations for Simple Harmonic Motion
Acceleration and SHM
Acceleration a and displacement x can be represented by the defining equation of SHM:
a ∝ −x
The acceleration of an object oscillating in simple harmonic motion is:
a = −⍵2x
Where:
a = acceleration (m s-2)
⍵ = angular frequency (rad s-1)
x = displacement (m)
This is used to find the acceleration of an object with a particular angular frequency ⍵ at a specific displacement x
The equation demonstrates:
The acceleration reaches its maximum value when the displacement is at a maximum i.e.. x = A (amplitude)
The minus sign shows that when the object is displaced to the right, the direction of the acceleration is to the left and vice versa (a and x are always in opposite directions to each other)
Displacement and SHM
The graph of acceleration against displacement is a straight line through the origin sloping downwards (similar to y = −x)

The acceleration of an object in SHM is directly proportional to the negative displacement
The key features of the graph are:
The gradient is equal to −⍵2
The maximum and minimum displacement x values are the amplitudes −A and +A
A solution to the SHM acceleration equation is the displacement equation:
x = A cos (⍵t)
Where:
A = amplitude (m)
t = time (s)
This occurs when:
An object is oscillating from its amplitude position (x = A or x = −A at t = 0)
The displacement will be at its maximum when cos(⍵t) equals 1 or −1, when x = A
This equation can be used to find the position of an object in SHM with a particular angular frequency and amplitude at a moment in time
If an object is oscillating from its equilibrium position (x = 0 at t = 0) then the displacement equation will be:
x = A sin (⍵t)
The displacement will be at its maximum when sin(⍵t) equals 1 or −1, when x = A
This is because the sine graph starts at 0, whereas the cosine graph starts at a maximum
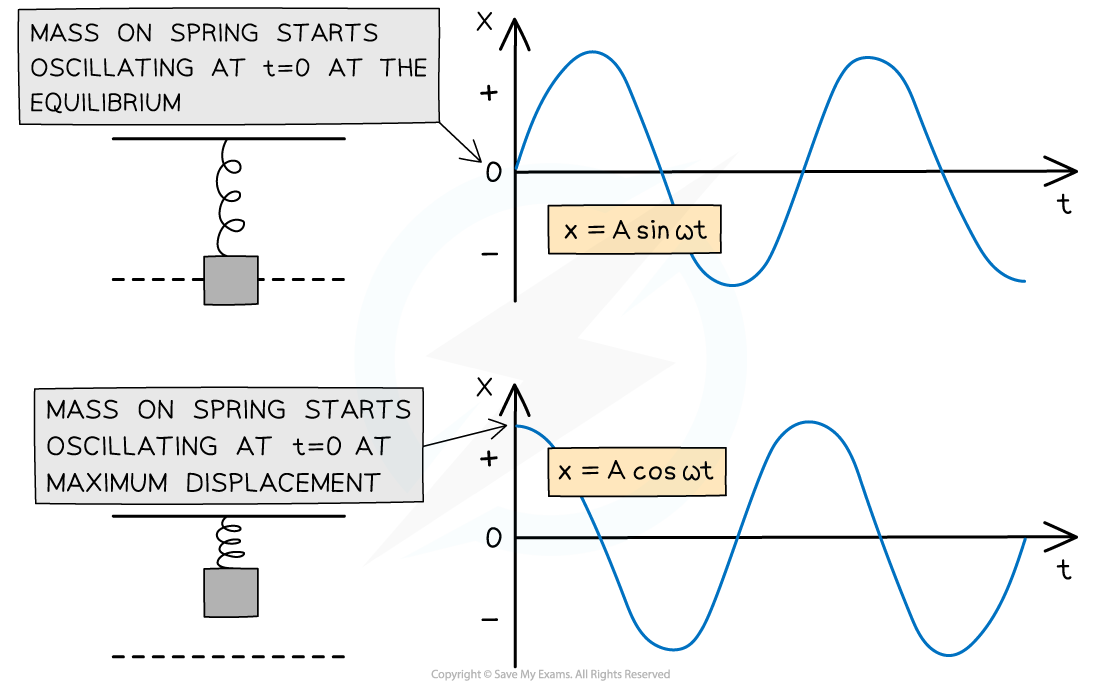
These two graphs represent the same SHM. The difference is the starting position
Worked Example
A mass of 55 g is suspended from a fixed point by means of a spring.
The stationary mass is pulled vertically downwards through a distance of 4.3 cm and then released at t = 0.
The mass is observed to perform simple harmonic motion with a period of 0.8 s.
Calculate the displacement x, in cm, of the mass at time t = 0.3 s.
Answer:
Step 1: Write down the SHM displacement equation
Since the mass is released at t = 0 at its maximum displacement, the displacement equation will be with the cosine function:
Step 2: Calculate angular frequency
Remember to use the value of the time period given, not the time passed
Step 3: Substitute values into the displacement equation
x = 4.3cos (7.85 × 0.3) = –3.0369… = –3.0 cm (2 s.f)
Make sure the calculator is in radians mode
The negative value means the mass is 3.0 cm on the opposite side of the equilibrium position to where it started (3.0 cm above it)
Speed and SHM
The speed of an object in simple harmonic motion varies as it oscillates back and forth
Its speed is the magnitude of its velocity
The greatest speed of an oscillator is at the equilibrium position ie. when its displacement x = 0
How the speed v changes with the oscillator’s displacement x in SHM is defined by:
Where:
v = speed (m s-1)
A = amplitude (m)
± = ‘plus or minus’. The value can be negative or positive
⍵ = angular frequency (rad s-1)
x = displacement (m)
This equation shows that when an oscillator has a greater amplitude A, it has to travel a greater distance in the same time and hence has greater speed v
Although the symbol v is commonly used to represent velocity, not speed, exam questions focus more on the magnitude of the velocity than its direction in SHM
Worked Example
A simple pendulum oscillates with simple harmonic motion with an amplitude of 15 cm.
The frequency of the oscillations is 6.7 Hz.
Calculate the speed of the pendulum at a position of 12 cm from the equilibrium position.
Answer:
Step 1: Write out the known quantities
Amplitude of oscillations, A = 15 cm = 0.15 m
Displacement at which the speed is to be found, x = 12 cm = 0.12 m
Frequency, f = 6.7 Hz
Step 2: Oscillator speed with displacement equation
Since the speed is being calculated, the ± sign can be removed as direction does not matter in this case
Step 3: Write an expression for the angular frequency
Equation relating angular frequency and normal frequency:
Step 4: Substitute in values and calculate
v = 3.789 = 3.8 m s-1 (2 s.f)
Examiner Tips and Tricks
Since displacement is a vector quantity, remember to keep the minus sign in your solutions if they are negative, you could lose a mark if not! Also, remember that your calculator must be in radians mode when using the cosine and sine functions. This is because the angular frequency ⍵ is calculated in rad s-1, not degrees. You often have to convert between time period T, frequency f and angular frequency ⍵ for many exam questions – so make sure you revise the equations relating to these.
Ready to test your students on this topic?
- Create exam-aligned tests in minutes
- Differentiate easily with tiered difficulty
- Trusted for all assessment types

Did this page help you?