Conditions for Simple Harmonic Motion (Edexcel A Level Physics): Revision Note
Exam code: 9PH0
Conditions for Simple Harmonic Motion
Simple harmonic motion (SHM) is a specific type of oscillation
An oscillation is said to be SHM when:
The acceleration is proportional to the displacement
The acceleration is in the opposite direction to the displacement
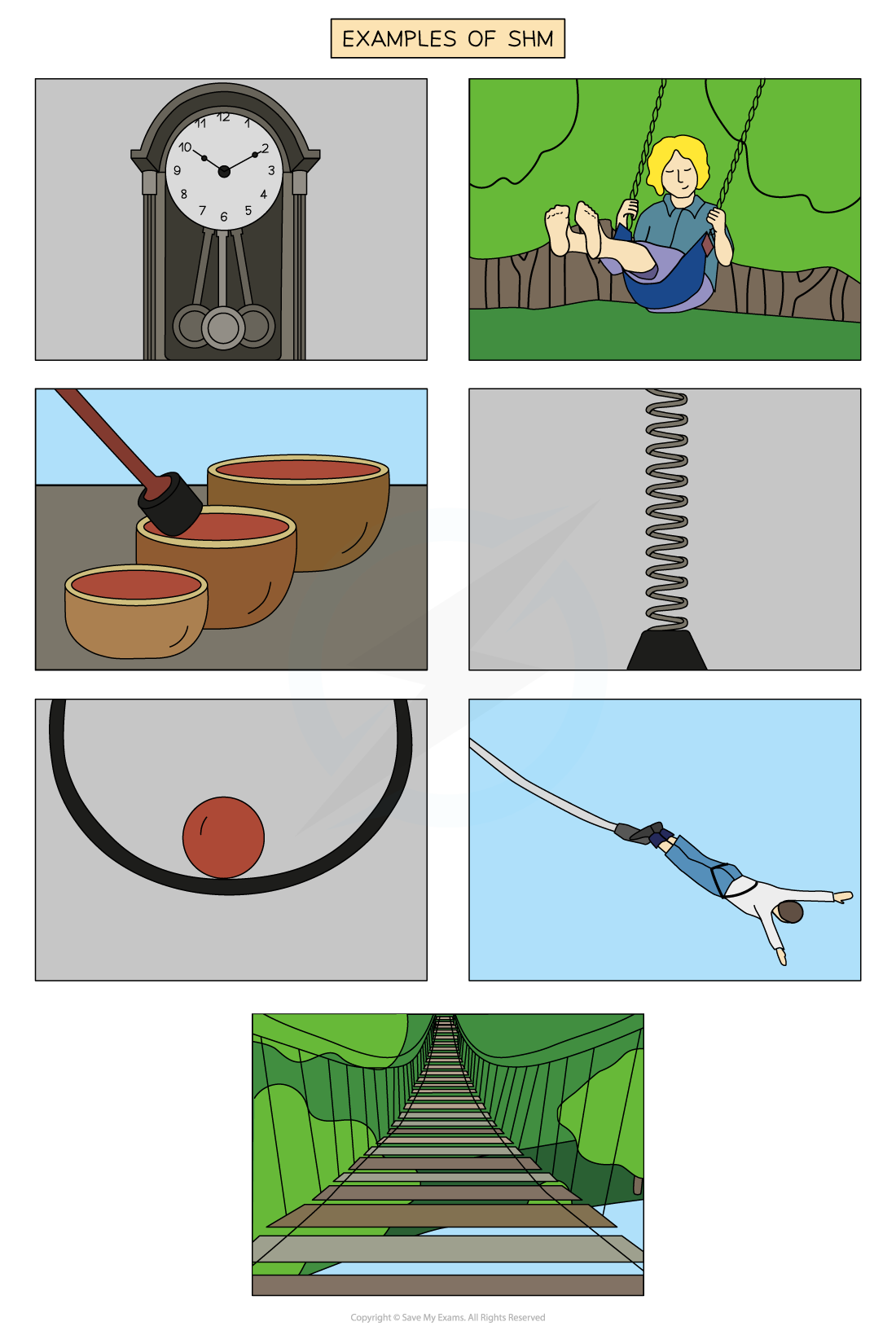
Examples of oscillators that undergo SHM are:
The pendulum of a clock
A mass on a spring
Guitar strings
The electrons in alternating current flowing through a wire
Time period, T:
The objects swings are periodic, meaning they are repeated in regular intervals according to their frequency or time period
If an object swings freely it always takes the same time to complete one swing
Restoring force
When an object is moving in SHM a force, called the restoring force, F, is always trying to return the object back to its equilibrium position.
The force is proportional to the displacement, x, from that equilibrium position
F = -kx
Where:
F is the restoring force
x is the displacement of the object from the equilibrium position
k is a constant depending on the system
the negative sign shows that the acceleration will always be towards the centre of oscillation
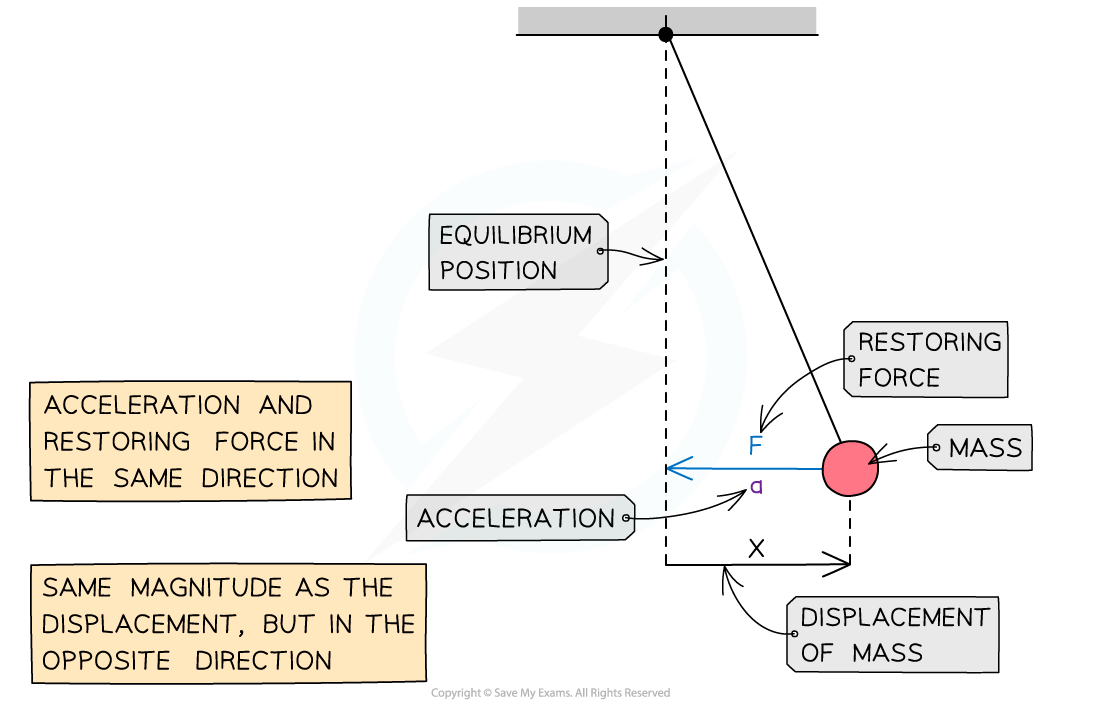
Force, acceleration and displacement of a pendulum in SHM
This is why a person jumping on a trampoline is not an example of simple harmonic motion:
The restoring force on the person is not proportional to their distance from the equilibrium position
When the person is not in contact with the trampoline, the restoring force is equal to their weight, which is constant
This does not change, even if they jump higher
Worked Example
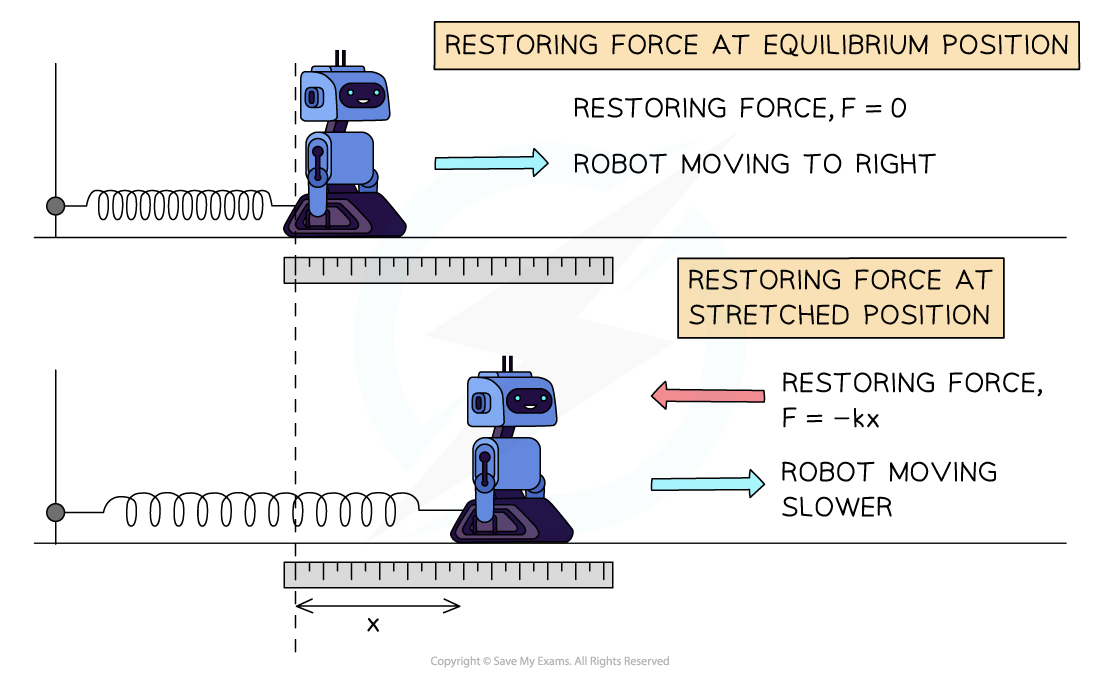
A 200g toy robot is attached to a pole by a spring, with a spring constant of 90 N m-1, and made to oscillate horizontally.
(a) What force will act on the robot when it is at its amplitude position of 5 cm from equilibrium?
(b) How fast will the robot accelerate whilst at this amplitude position?
Answer:
Part (a)
Step 1: Convert amplitude into m
5 cm = 0.05 m
Step 2: Substitute values into the restoring force equation
F = -kx = -(90) x (0.05) = - 4.5 N
Step 3: Explain the answer
A force of 4.5 newtons will act on the robot, trying to pull it back towards the equilibrium position.
Part (b)
Step 1: Convert mass of robot into kg
200 g = 0.2 kg
Step 2: Substitute values into Newton's second law equation:
F = ma
So, =
= -22.5 m s-2
Step 3: Explain the answer
The robot will decelerate at a rate of 22.5 m s-2 when at this amplitude position
Examiner Tips and Tricks
Even with this topic you must make sure you convert all quantities into standard SI units

Unlock more, it's free!
Did this page help you?