IBMathsDPAnalysis & Approaches (AA)SLRevision Notes3. Geometry & TrigonometryTrigonometryPythagoras & Right-Angled Trigonometry

Pythagoras & Right-Angled Trigonometry (DP IB Analysis & Approaches (AA)): Revision Note

Amber

Written by: Amber

Reviewed by: Dan Finlay

Updated on

DP Analysis & Approaches (AA): SLDP Applications & Interpretation (AI): HLDP Applications & Interpretation (AI): SLDP Analysis & Approaches (AA): HL

Did this video help you?

Pythagoras

What is the Pythagorean theorem?

  • Pythagoras’ theorem is formula using the lengths of the sides of a right-angled triangle

  • The square of the hypotenuse is equal to the sum of the squares of the two shorter sides

  • The formula can be written as a squared plus b squared equals c squared

    • a and b are the lengths of the shorter sides

    • c is the length of the hypotenuse

  • To find the length of the hypotenuse:

    • Use c equals square root of a squared plus b squared end root

  • To find the length of a shorter side:

    • Use a equals square root of c squared minus b squared end root

  • The converse of the theorem is true

    • If a squared plus b squared equals c squared

    • Then the triangle has a right-angle

Right-angled triangle with sides labelled a, b, and hypotenuse c; angle between a and b is a right angle.
Example of right-angled triangle

Examiner Tips and Tricks

The formula for Pythagoras' theorem is not given in the formula booklet.

Worked Example

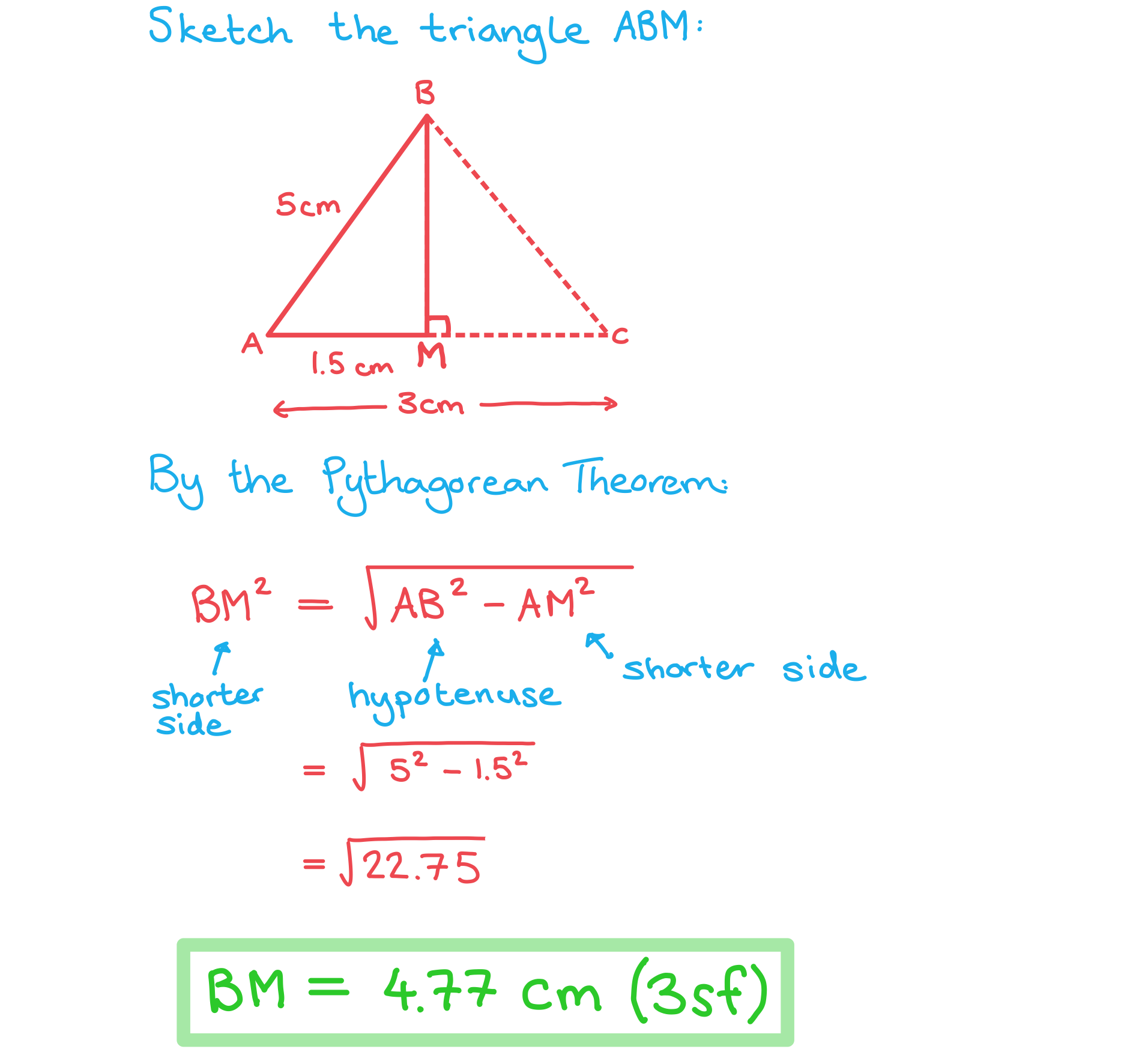
ABCDEF is a chocolate bar in the shape of a triangular prism.  The end of the chocolate bar is an isosceles triangle where AC = 3 cm and AB = BC = 5 cm.  M is the midpoint of AC. This information is shown in the diagram below.

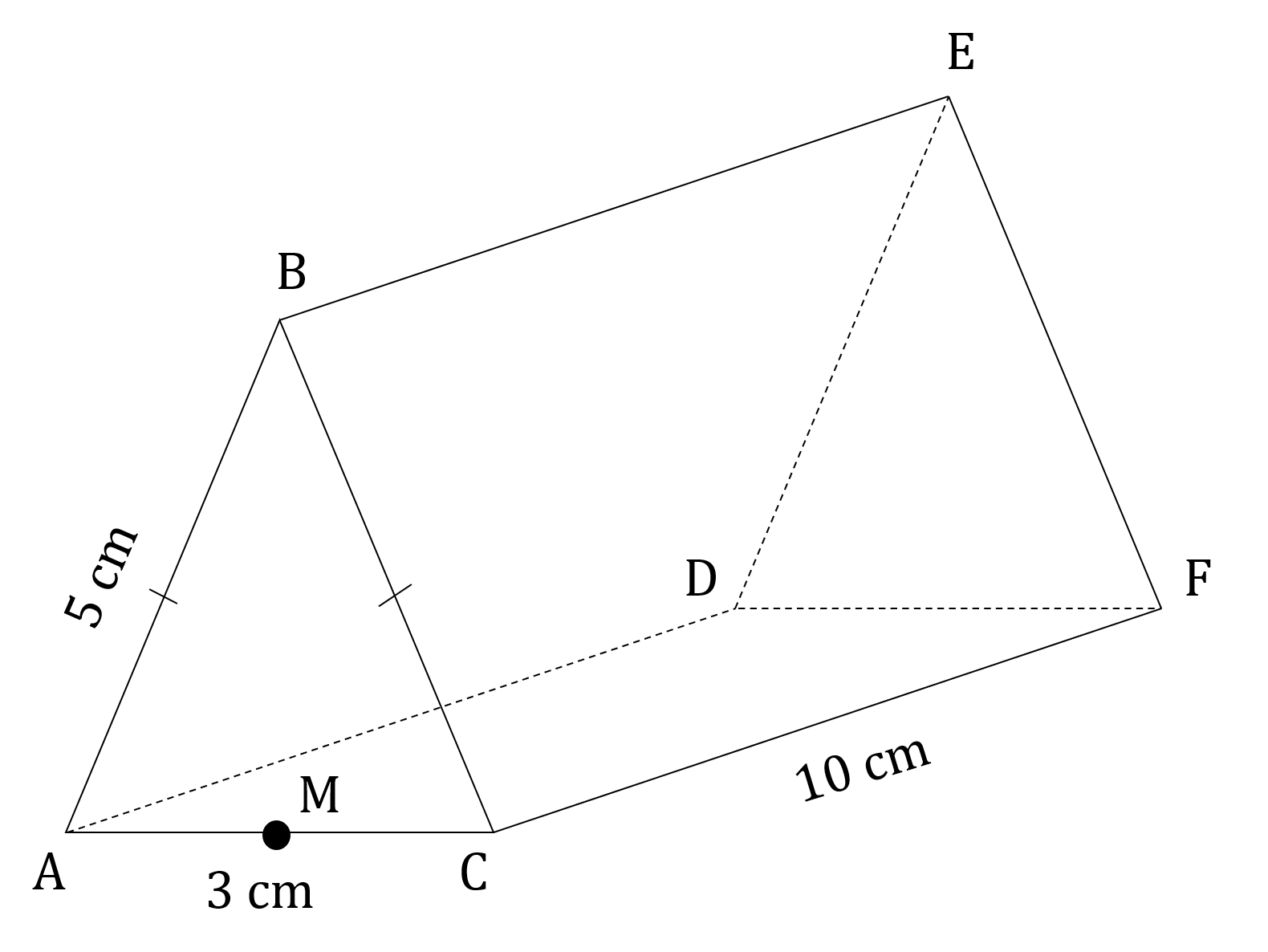
diagram-for-we-3-3-1-pythag

Calculate the length BM.

3-3-1-ai-sl-pythag-we-solution

Did this video help you?

Right-Angled Trigonometry

What is right-angled trigonometry?

  • Right-angled trigonometry is used to find the angles and the lengths of the sides of a right-angled triangle

  • Three trigonometric functions are used to show the ratios between different pairs of sides

    • sine (sin)

    • cosine (cos)

    • tangent (tan)

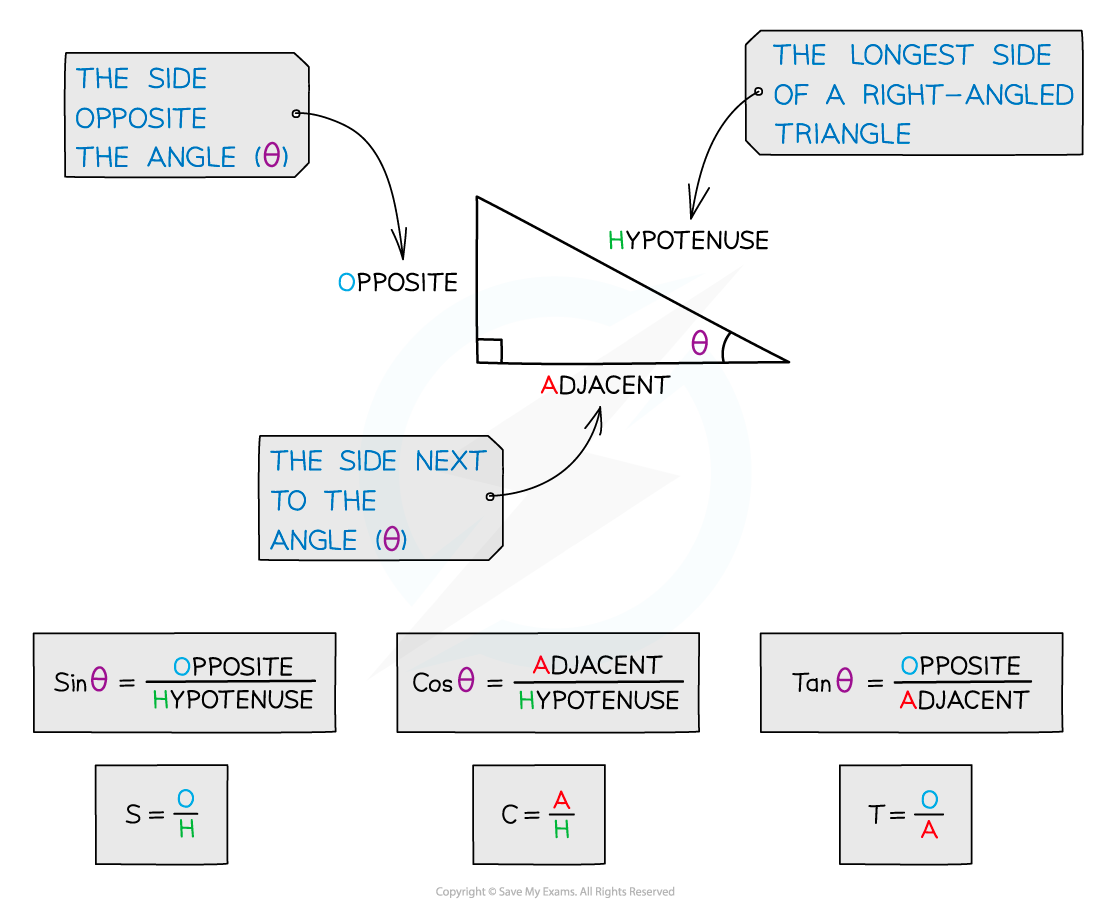
What are the formulas for sin, cos and tan?

  • You need to label one angle and all three sides of the right-angled triangle

    • theta is one of the acute angles

    • H is the length of the hypotenuse

    • O is the length of the side opposite theta

    • A is the length of the side adjacent to theta

Two right-angled triangles; left triangle with angle θ, hypotenuse H, opposite O, adjacent A. Right triangle similar, rotated counterclockwise.
Example of labelling a right-angled triangle

  • The formulas for sin, cos and tan are:

    • sin space theta blank equals space opposite over hypotenuse space equals space O over H

    •  cos space theta blank equals space adjacent over hypotenuse space equals space A over H

    • tan space theta blank equals space opposite over adjacent space equals space O over A

Diagram of a right-angled triangle with labels for hypotenuse, opposite, and adjacent sides; includes trigonometric ratios: sine, cosine, tangent.

Examiner Tips and Tricks

The mnemonic SOHCAHTOA is often used as a way of remembering the formulas. These are not given in the formula booklet.

How can I use SOHCAHTOA to find missing lengths and angles?

  • STEP 1
    Label the sides of the triangle as H, O and A

  • STEP 2
    Identify which trigonometric ratio to use: sin, cos or tan

    • Write down the letters of the length you are given or want to find

    • Find the two letters in SOHCAHTOA to identify which ratio to use

      • If you have A and H then use cos

  • STEP 3
    Substitute the values into the relevant trigonometric formula

    • Remember to put brackets around the angle

      • sin open parentheses 50 close parentheses equals straight A over 7  or  cos open parentheses 40 close parentheses equals 3 over straight H or tan open parentheses theta close parentheses equals 3 over 7

  • STEP 4
    Rearrange and solve for the unknown letter

    • You will either need to multiply or divide to find a missing length

      • sin open parentheses 50 close parentheses equals straight A over 7 leads to straight A equals 7 cross times sin open parentheses 50 close parentheses

      • cos open parentheses 40 close parentheses equals 3 over straight H leads to straight H equals fraction numerator 3 over denominator cos open parentheses 40 close parentheses end fraction

    • You will need to use the inverse trigonometric functions to find a missing angle

      • tan open parentheses theta close parentheses equals 3 over 7 leads to theta equals tan to the power of negative 1 end exponent open parentheses 3 over 7 close parentheses

Worked Example

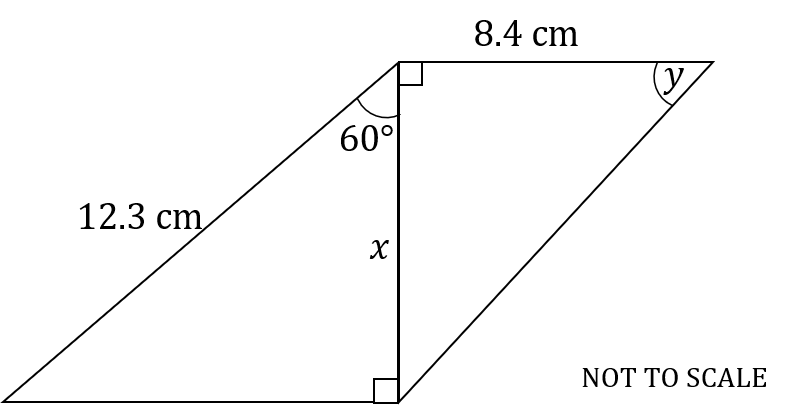
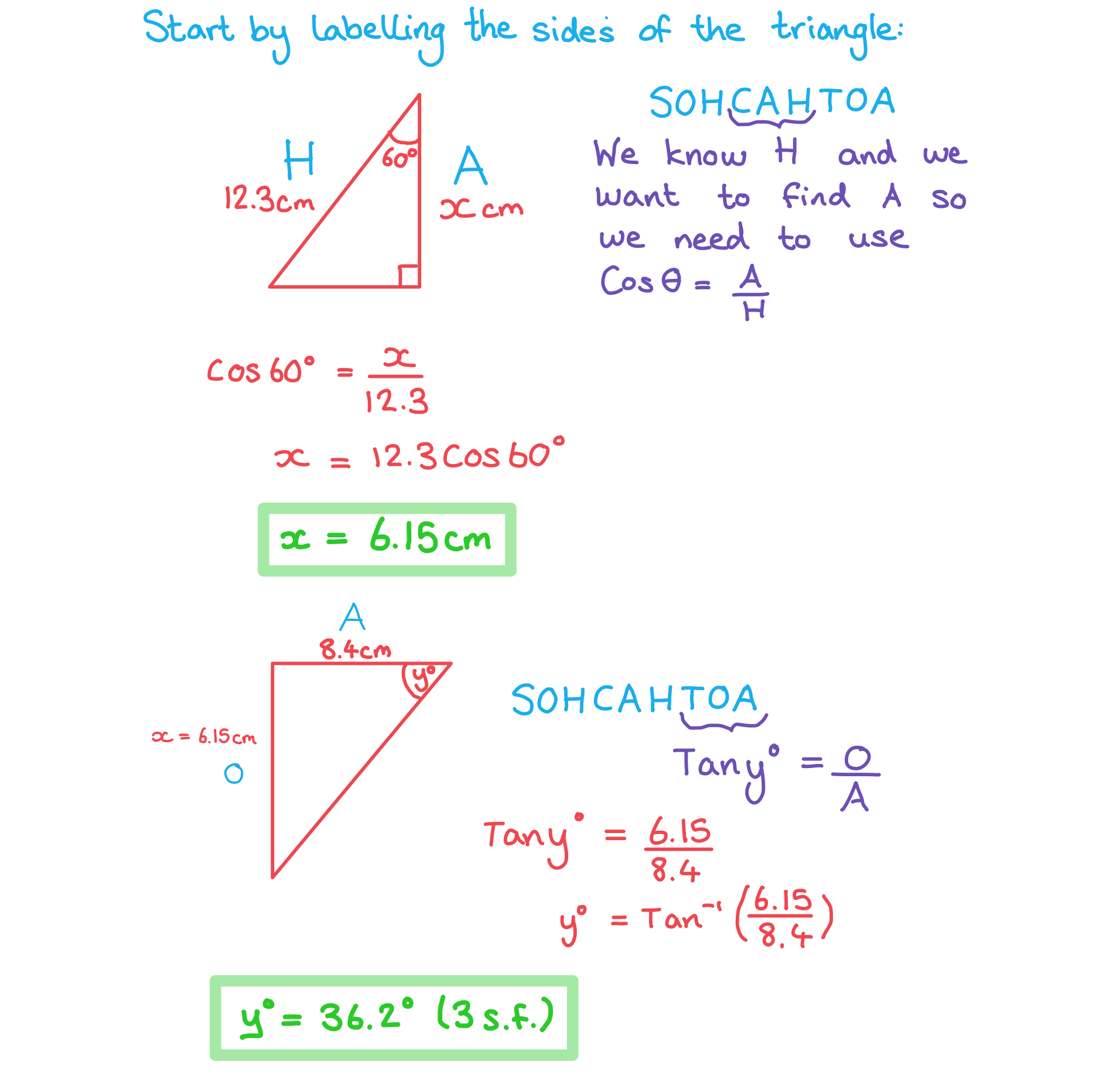
Find the values of x and y in the following diagram. Give your answers to 3 significant figures.

sa-diagram-for-we-3-3-1-trig
3-3-1-ai-sl-r-a-trig-we-solution

Did this video help you?

3D Problems

Can I use Pythagoras' theorem and trigonometry in 3D?

  • You can break a 3D problem into 2D triangles

  • The formula for the length of the diagonal of a cuboid with dimensions a cross times b cross times c is d equals square root of a squared plus b squared plus c squared end root

    • This is sometimes referred to as the 3D version of Pythagoras' theorem

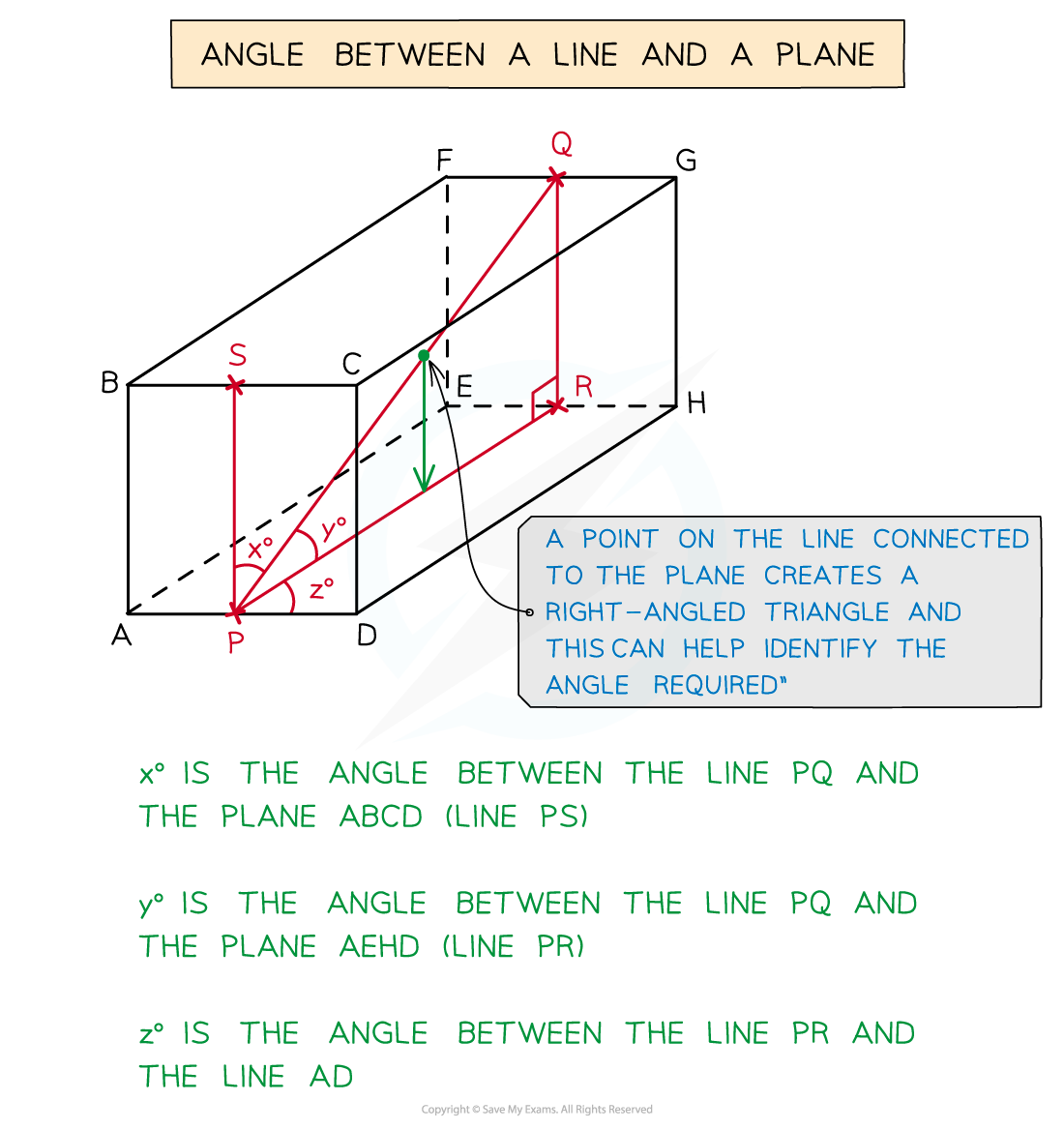
  • You can find missing angles by drawing right-angled triangles

    • You can find angles between lines and planes

Diagram showing the angle between a line PQ and planes in a 3D box, labelled with points, lines, and angles x°, y°, z°. Includes explanatory text.

Examiner Tips and Tricks

Draw a big enough sketch so that you can clearly annotate it with missing angles and lengths.

Worked Example

A pencil is being put into a cuboid shaped box. The base of the box has a width of 4 cm and a length of 6 cm. The height of the box is 3 cm. Find:

a) the length of the longest pencil that could fit inside the box,

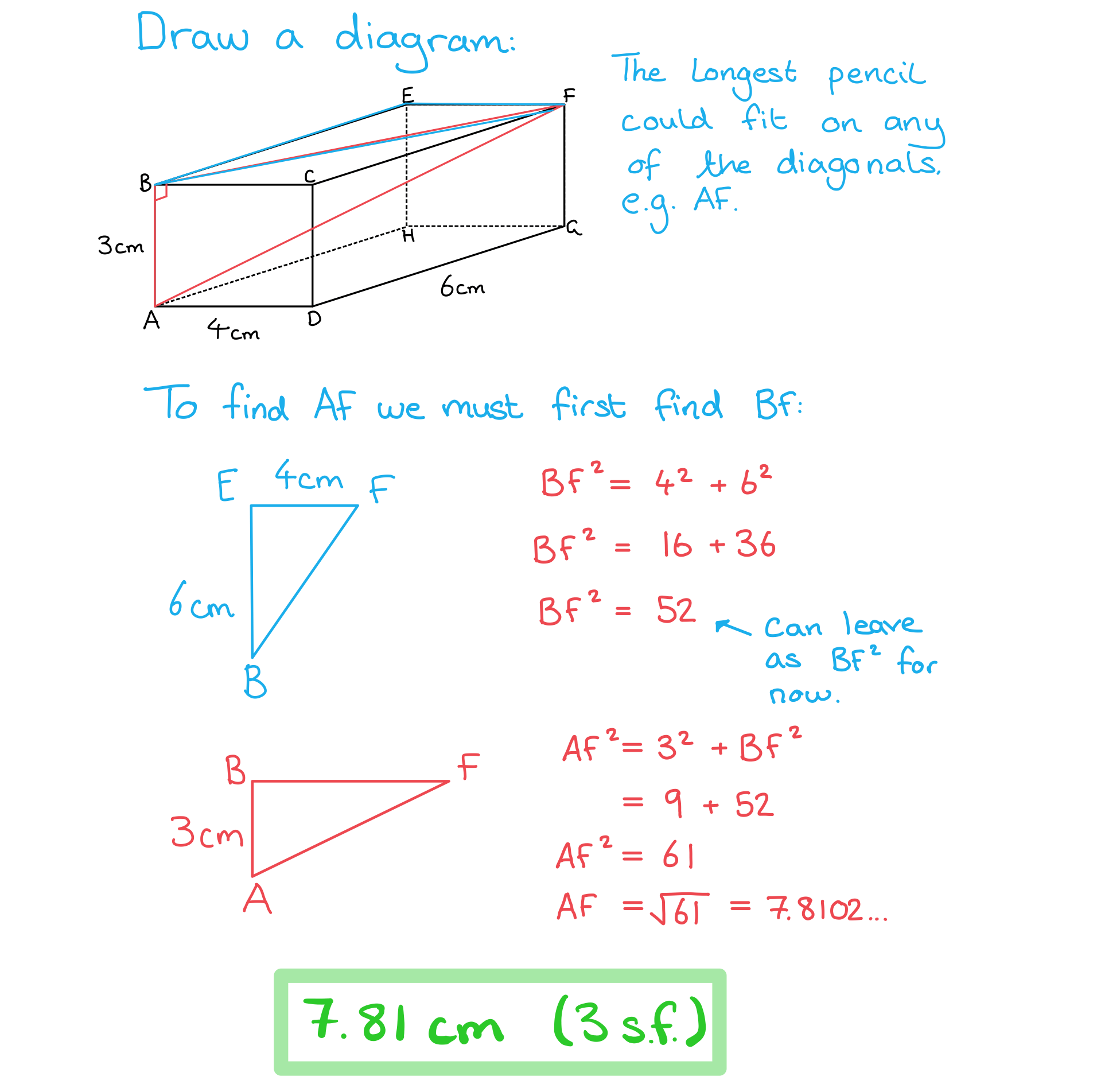
ai-sl-3-3-1-3d-pythag-trig-we-solution-a

 

b) the angle that the pencil would make with the top of the box.

ai-sl-3-3-1-3d-pythag-trig-we-solution-b
👀 You've read 1 of your 5 free revision notes this week
An illustration of students holding their exam resultsUnlock more revision notes. It’s free!

By signing up you agree to our Terms and Privacy Policy.

Already have an account? Log in

Test yourselfFlashcards

Did this page help you?

Previous:Volume & Surface AreaNext:Sine Rule, Cosine Rule & Area of a Triangle
Author
Reviewer
Amber

Author: Amber

Expertise: Maths Content Creator

Amber gained a first class degree in Mathematics & Meteorology from the University of Reading before training to become a teacher. She is passionate about teaching, having spent 8 years teaching GCSE and A Level Mathematics both in the UK and internationally. Amber loves creating bright and informative resources to help students reach their potential.

Dan Finlay

Reviewer: Dan Finlay

Expertise: Maths Subject Lead

Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

Download notes on Pythagoras & Right-Angled Trigonometry