Thermionic Emission (Edexcel International A Level (IAL) Physics): Revision Note
Exam code: YPH11
Thermionic Emission
When metals are heated, the conduction electrons within them gain energy
If these electrons gain sufficient energy, they are able to leave the surface of the metal
This is known as thermionic emission
This is similar to the photoelectric effect, but the energy absorbed by electrons in this case is due to thermal energy, rather than the energy absorbed by incident photons
Once electrons are released from a metal surface they may be accelerated by electric or magnetic fields
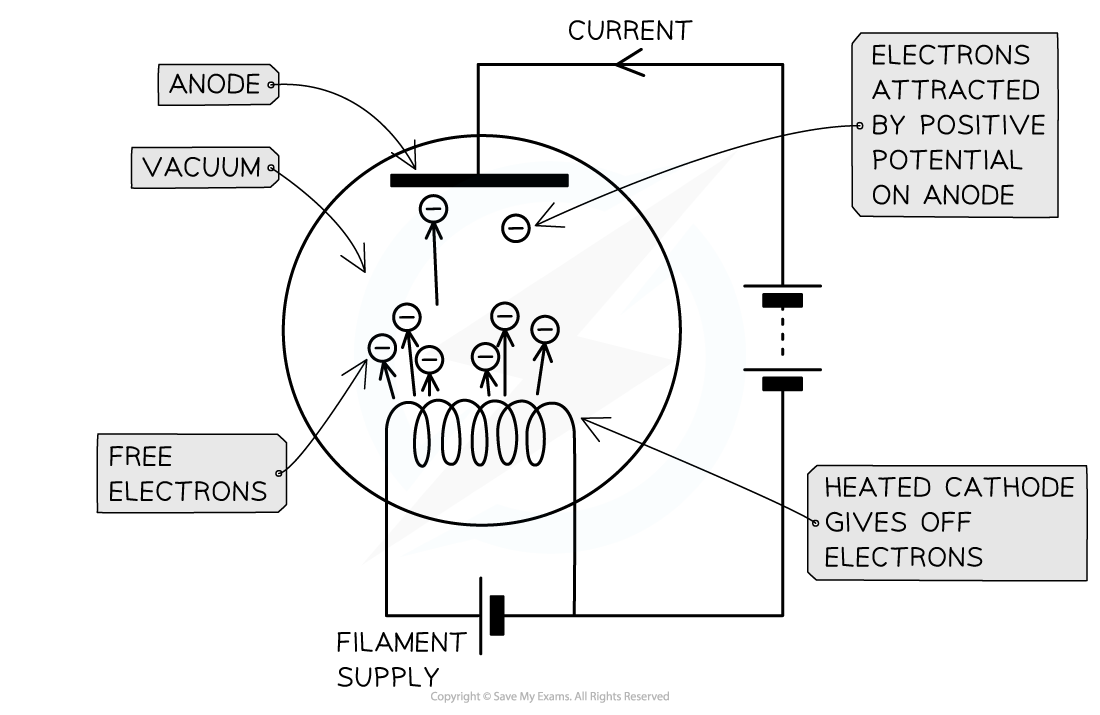
Electrons are emitted from the (negative) cathode and accelerated to the (positive) anode
Worked Example
Electron guns use electric fields to accelerate electrons to very high speeds.
Show that an electron accelerated from rest across a potential difference of 5.0 kV attains a speed of 4.2 × 107 m s–1.
Use the following data:
Mass of an electron me = 9.11 × 10–31 kg
Electron charge e = 1.6 × 10–19 C
Answer:
Step 1: List the known quantities
Potential difference = 5 kV = 5000 V
Mass of an electron, me = 9.11 × 10–31 kg
Electron charge e = 1.6 × 10–19 C
Step 2: Equate the kinetic energy gained by the electron to the energy transferred across the potential difference
Potential difference V is the energy transferred W per unit of charge Q, or
Since the charge in this case is an electron, Q = e and so W = eV
Therefore, the kinetic energy gained is equal to eV so we can write:
Step 3: Make speed v the subject of the equation
Rearranging this equation for v gives:
Step 4: Substitute quantities and calculate the speed v
Substituting known quantities gives:
= 41 908 313... = 4.2 × 107 m s–1
Examiner Tips and Tricks
Examiners commonly test if candidates can equate the energy gained across a potential difference with the kinetic energy of a particle, as we did here. Make sure you can combine the equations for kinetic energy and potential energy in order to calculate speed like we did here!

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?