Magnetic Force on a Current-Carrying Conductor (Edexcel International A Level (IAL) Physics): Revision Note
Exam code: YPH11
Magnetic Force on a Current-Carrying Conductor
A current-carrying conductor produces its own magnetic field
An external magnetic field will therefore exert a magnetic force on it
A current-carrying conductor (eg. a wire) will experience the maximum magnetic force if the current through it is perpendicular to the direction of the magnetic flux lines
A simple situation would be a copper rod placed within a uniform magnetic field
When current is passed through the copper rod, it experiences a force which makes it accelerate
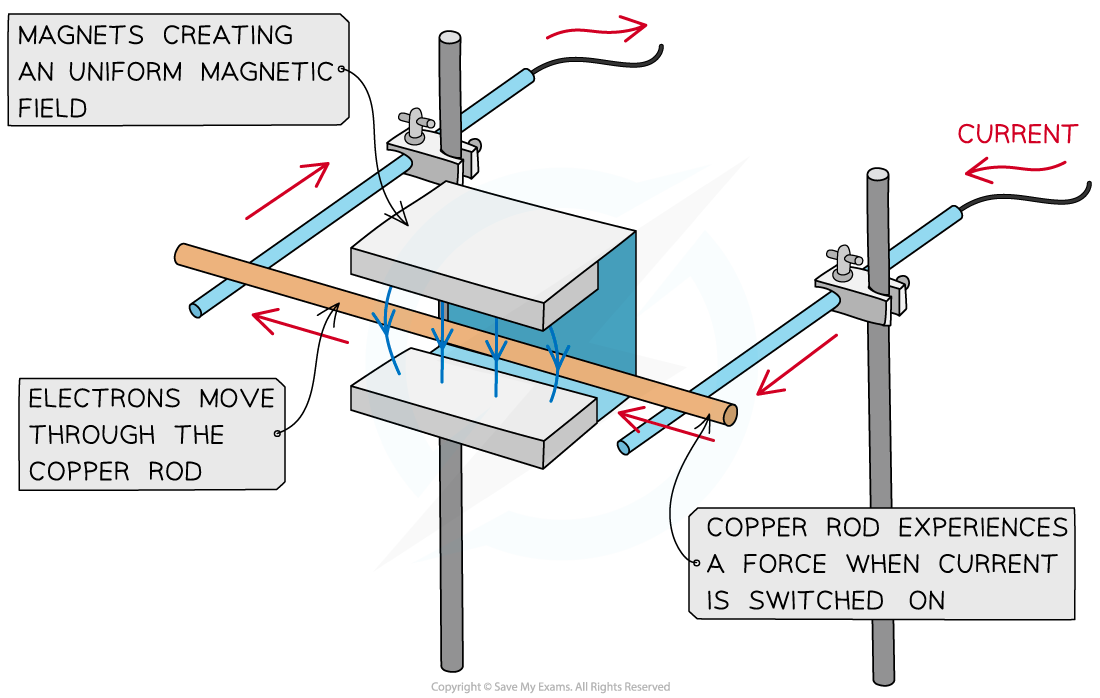
A copper rod moves within a magnetic field when current is passed through it
The force F on a conductor carrying current I in a magnetic field with flux density B is defined by the equation
F = BIL sin θ
Where:
F = magnetic force on the current-carrying conductor (N)
B = magnetic flux density of external magnetic field (T)
I = current in the conductor (A)
L = length of the conductor in the field (m)
θ = angle between the conductor and external flux lines (degrees)
This equation shows that the magnitude of the magnetic force F is proportional to:
Current I
Magnetic flux density B
Length of conductor in the field L
The sine of the angle θ between the conductor and the magnetic flux lines
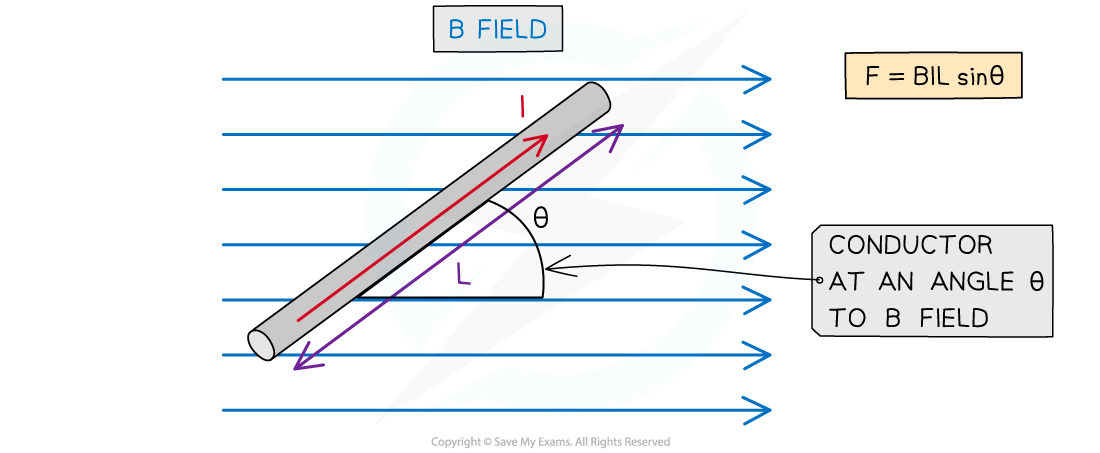
Magnitude of the force on a current carrying conductor depends on the angle of the conductor to the external B field
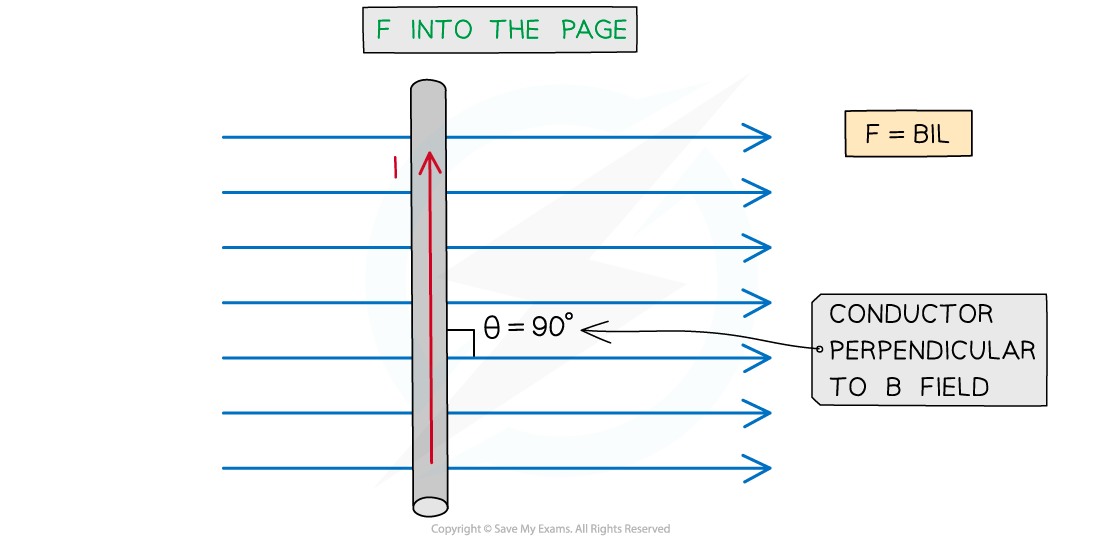
The maximum force occurs when sin θ = 1
This means θ = 90o and the conductor is perpendicular to the B field
This equation for the magnetic force now becomes:
F = BIL
The minimum force (0) is when sin θ = 0
This means θ = 0o and the conductor is parallel to the B field
It is important to note that a current-carrying conductor will experience no force if the current in the conductor is parallel to the field
Worked Example
A current of 0.87 A flows in a wire of length 1.4 m placed at 30o to a magnetic field of flux density 80 mT.
Calculate the force on the wire.
Answer:
Step 1: Write down the known quantities
Magnetic flux density, B = 80 mT = 80 × 10-3 T
Current, I = 0.87 A
Length of wire, L = 1.4 m
Angle between the wire and the magnetic flux lines, θ = 30o
Step 2: Write down the equation for the magnetic force on a current-carrying conductor
F = BIL sin θ
Step 3: Substitute in values and calculate
F = (80 × 10-3) × (0.87) × (1.4) × sin (30) = 0.04872 = 0.049 N (2 s.f)
Examiner Tips and Tricks
Remember that the direction of current is the flow of positive charge (i.e. conventional current) and this is in the opposite direction to the flow of electrons (i.e. electron flow)!
Fleming's Left Hand Rule for a Current-Carrying Conductor
Fleming's Left Hand Rule was previously used to determine the direction of the magnetic force on a moving charged particle in a magnetic field
It can also be used to determine the direction of the magnetic force on a current-carrying conductor in a magnetic field
This is because inside a conductor (e.g. a wire) there are many charged particles flowing as a current
As a reminder, the image representing Fleming's Left Hand Rule is shown below:
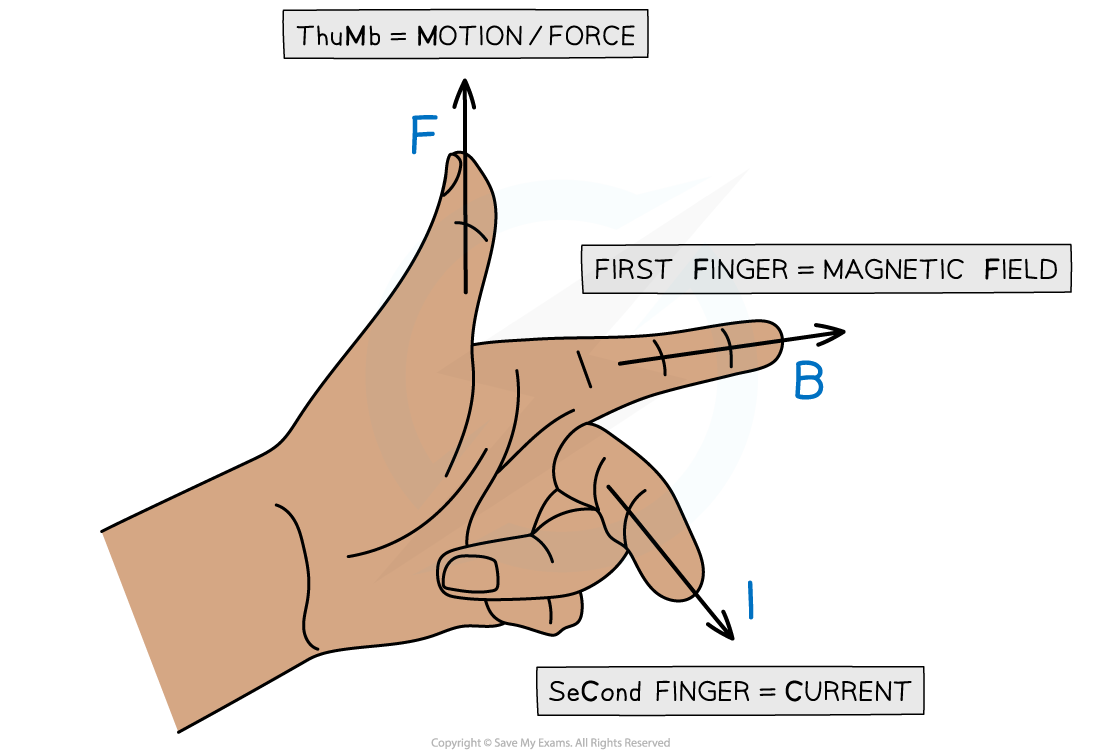
Fleming's Left Hand Rule. Remember, current is the flow of conventional current (i.e. positive to negative)
Using the conventional symbols representing vectors like magnetic flux density B and force F that go into the page (arrows) or out of the page (dots) we can apply Fleming's Left Hand Rule to problems in 3D
Worked Example
A current flows perpendicularly to a uniform magnetic field as shown in the diagram below.
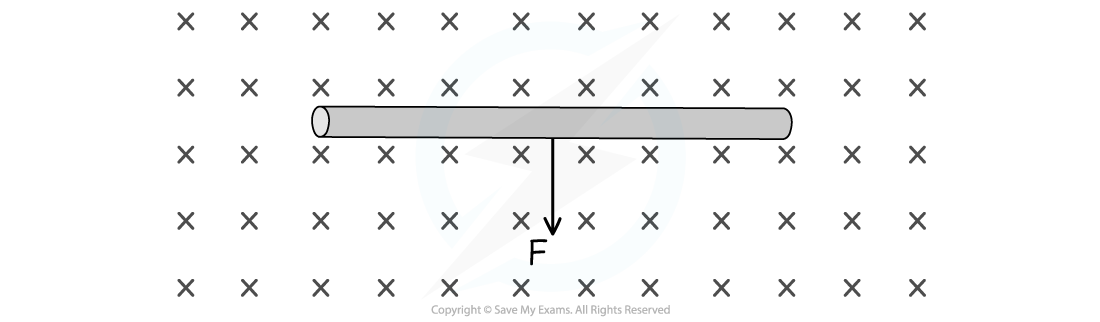
As a result, the conductor carrying the current experiences a magnetic force, F.
Determine the direction of the current flowing in the conductor.
Answer:
Step 1: Apply the instructions for Fleming's Left Hand Rule
Using Fleming’s Left Hand Rule for the quantities given:
First finger is the magnetic field, B = into the page (or screen!)
Thumb is the direction of the magnetic force F = vertically downwards
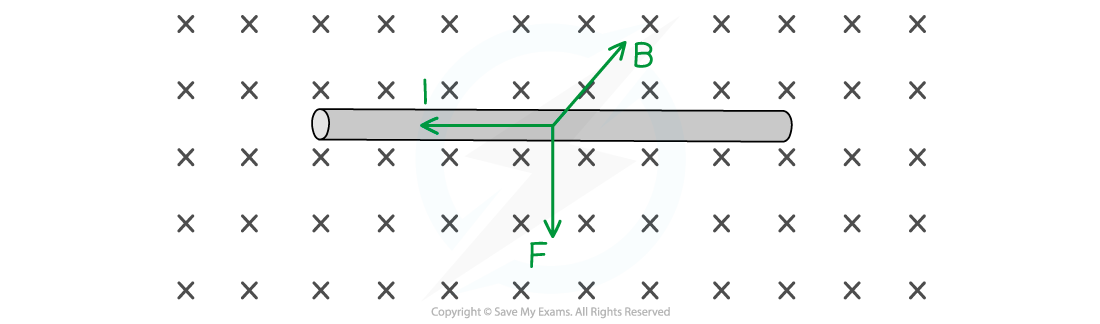
Step 2: Determine the direction of the conventional current
The first finger should be pointing into the page (or screen!) along the direction of the field
Rotating the entire hand allows the thumb to point downwards, along the direction of force
The second finger should be pointing towards the left of the page (or screen!)
This is the direction of conventional current in the wire, i.e., from right to left
Examiner Tips and Tricks
You will certainly need to apply Fleming's Left Hand Rule in your examination, at some point, whenever there is a current or charge flowing in a magnetic field. Remember, it is used to give the direction of either the magnetic force F, the magnetic field B, or the conventional current (or flow of positive charge) I.
As ever, you will gain more confidence twisting your arm in funny positions with three fingers at right-angles the more questions you practise: the more, the better!

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?