Properties of Waves (DP IB Physics): Revision Note
Properties of Waves
Travelling waves are defined as:
Oscillations that transfer energy from one place to another without transferring matter
Waves transfer energy, not matter
Waves are generated by oscillating sources
These oscillations travel away from the source
Oscillations can propagate through a medium (e.g. air, water) or in a vacuum (i.e. no particles), depending on the type of wave
The key properties of travelling waves are:
displacement
wavelength
amplitude
period
frequency
wave speed
Displacement
Displacement
of a wave is the distance of a point on the wave from its equilibrium position
It is a vector quantity; it can be positive or negative
Measured in metres (m)
Wavelength
Wavelength λ is the length of one complete oscillation measured from the same point on two consecutive waves
For example, two crests, or two troughs
Measured in metres (m)
Amplitude
Amplitude A is the maximum displacement of an oscillating wave from its equilibrium position (x = 0)
Amplitude can be positive or negative depending on the direction of the displacement
Measured in metres (m)
Where the wave has 0 amplitude (the horizontal line) is referred to as the equilibrium position

Diagram showing the amplitude and wavelength of a wave
Period and frequency
Period (T) is the time taken for a complete oscillation to pass a fixed point
Measured in seconds (s)
Frequency (f) is the number of complete oscillations to pass a fixed point per second
Measured in Hertz (Hz)
The frequency, f, and the period, T, of a travelling wave are related to each other by the equation:
Where:
f = frequency (Hz)
T = time period (s)

Period T and frequency f of a travelling wave
Wave speed
Wave speed (v) is the distance travelled by the wave per unit time
Measured in metres per second (m s-1)
The wave speed is defined by the equation:
Where:
v = wave speed (m s–1)
λ = wavelength (m)
This is referred to as the wave equation
It tells us that for a wave of constant speed:
As the wavelength increases, the frequency decreases
As the wavelength decreases, the frequency increases
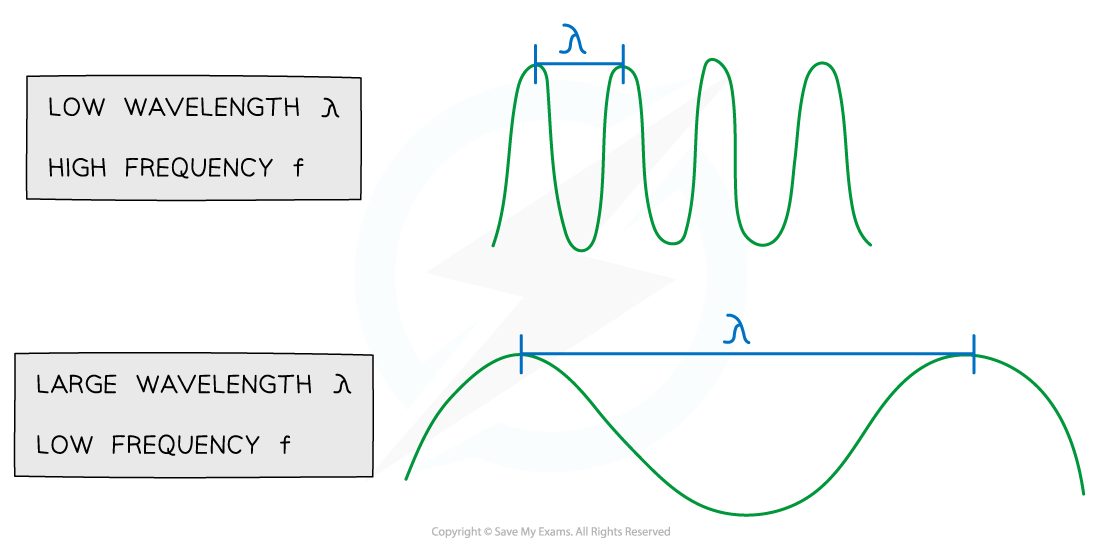
The relationship between the frequency and wavelength of a wave
Worked Example
The graph below shows a travelling wave.

Determine:
(a) The amplitude A of the wave, in m.
(b) The frequency f of the wave, in Hz.
Answer:
(a) Identify the amplitude A of the wave on the graph
The amplitude is defined as the maximum displacement from the equilibrium position (x = 0)
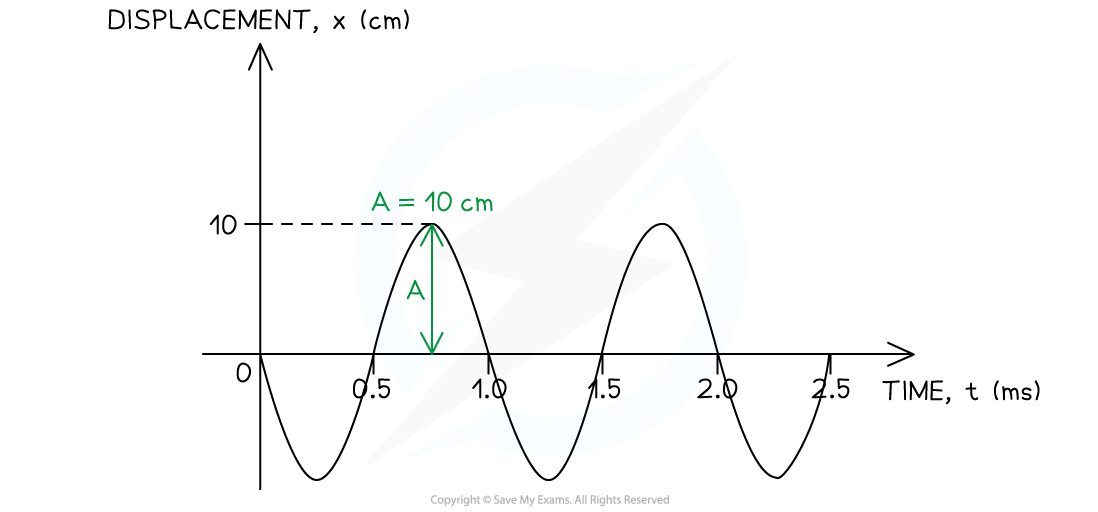
The amplitude must be converted from centimetres (cm) into metres (m)
A = 0.1 m
(b) Calculate the frequency of the wave
Step 1: Identify the period T of the wave on the graph
The period is defined as the time taken for one complete oscillation to occur

The period must be converted from milliseconds (ms) into seconds (s)
T = 1 × 10–3 s
Step 2: Write down the relationship between the frequency f and the period T
Step 3: Substitute the value of the period determined in Step 1
Worked Example
The wave in the diagram below has a speed of 340 m s–1.
Determine the wavelength of the wave.
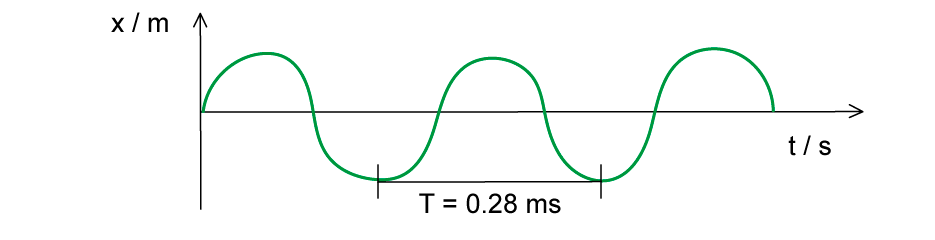
Answer:

Worked Example
A travelling wave has a period of 1.0 μs and travels at a velocity of 100 cm s–1.
Calculate the wavelength of the wave, in m.
Answer:
Step 1: Write down the known quantities
Period, T = 1.0 μs = 1.0 × 10–6 s
Velocity, v = 100 cm s–1 = 1.0 m s–1
Note the conversions:
The period must be converted from microseconds (μs) into seconds (s)
The velocity must be converted from cm s–1 into m s–1
Step 2: Write down the relationship between the frequency f and the period T
Step 3: Substitute the value of the period into the above equation to calculate the frequency
Step 4: Write down the wave equation
Step 5: Rearrange the wave equation to calculate the wavelength λ
Step 6: Substitute the numbers into the above equation
Examiner Tips and Tricks
You must be able to interpret different properties of waves from a variety of graphs. You may recognise that calculating the time period and wavelength looks very similar (the distance for one full wave). This is the time period if the x-axis is time. If the x-axis is distance, then this distance is the wavelength.
Pay very close attention to units. If you want a frequency in Hertz, then the time period must be in seconds and not milliseconds.

Unlock more, it's free!
Did this page help you?