Area of a Triangle (Edexcel GCSE Maths): Revision Note
Exam code: 1MA1
Did this video help you?
Area of a triangle
How do I find the area of a non-right-angled triangle?
The area of any triangle can be found using the formula
C is the angle between sides
and
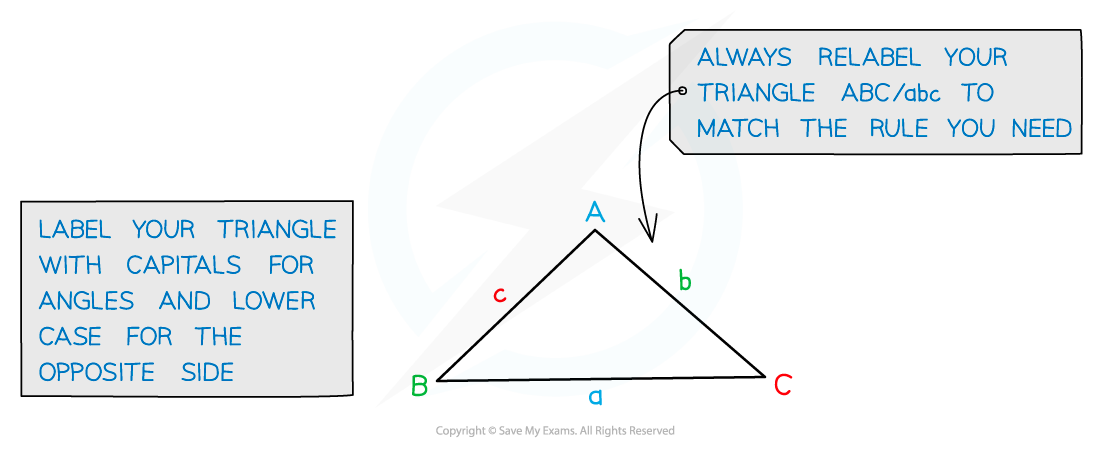
Label your triangle correctly
Make sure that C is always the angle between the two sides
If angle C is 90°, you get a right-angled triangle
sin 90° = 1 so the formula becomes the familiar "Area = ½ × base × height"!
Examiner Tips and Tricks
You are given the triangle area rule on the formula sheet
Worked Example
The following diagram shows triangle .
,
and angle
.
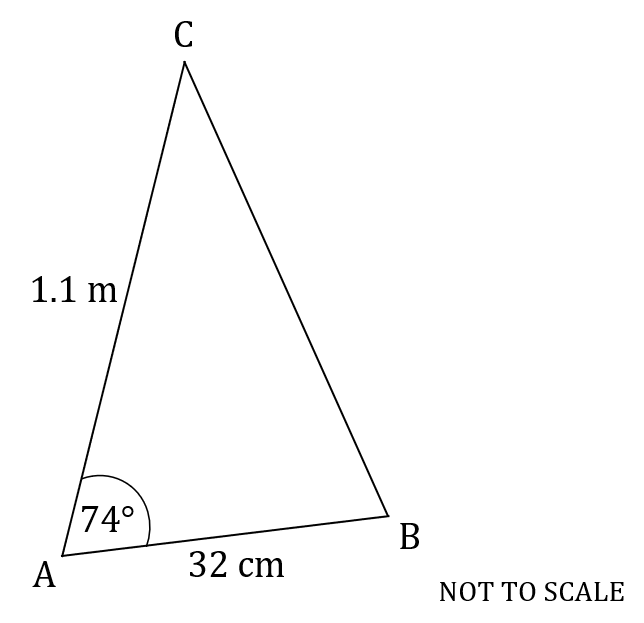
Calculate the area of triangle, giving your answer in m2.
Label the sides of the triangle
Convert the sides to be in the same units

Use the area of a triangle formula,
The area is 0.169 m2 (to 3 s.f.)

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?