Prime Factor Decomposition (Cambridge (CIE) IGCSE Maths): Revision Note
Exam code: 0580 & 0980
Did this video help you?
Prime factor decomposition
What are prime factors?
A factor of a given number is a value that divides the given number exactly, with no remainder
e.g. 6 is a factor of 18
A prime number is a number which has exactly two factors; itself and 1
e.g. 5 is a prime number, as its only factors are 5 and 1
You should remember the first few prime numbers:
2, 3, 5, 7, 11, 13, 17, 19, …
The prime factors of a number are therefore all the primes which multiply to give that number
e.g. The prime factors of 30 are 2, 3, and 5
2 × 3 × 5 = 30
How do I find prime factors?
Use a factor tree to find prime factors
Split the number up into a pair of factors
Then split each of those factors up into another pair
Continue splitting up factors along each "branch" until you get to a prime number
These can not be split into anything other than 1 and themselves
It helps to circle the prime numbers at the end of the branches

A number can be uniquely written as a product of prime factors
Write the prime factors as a multiplication, in ascending order
360 = 2 × 2 × 2 × 3 × 3 × 5
This can then be written more concisely using powers
360 = 23 × 32 × 5
A question asking you to do this will usually be phrased as "Express … as the product of its prime factors"
Worked Example
Write 432 as the product of its prime factors.
Create a factor tree
Start with 432 and choose any two numbers that multiply together to make 432

Repeat this for the two factors, until all of the values are prime numbers and cannot be broken down any further
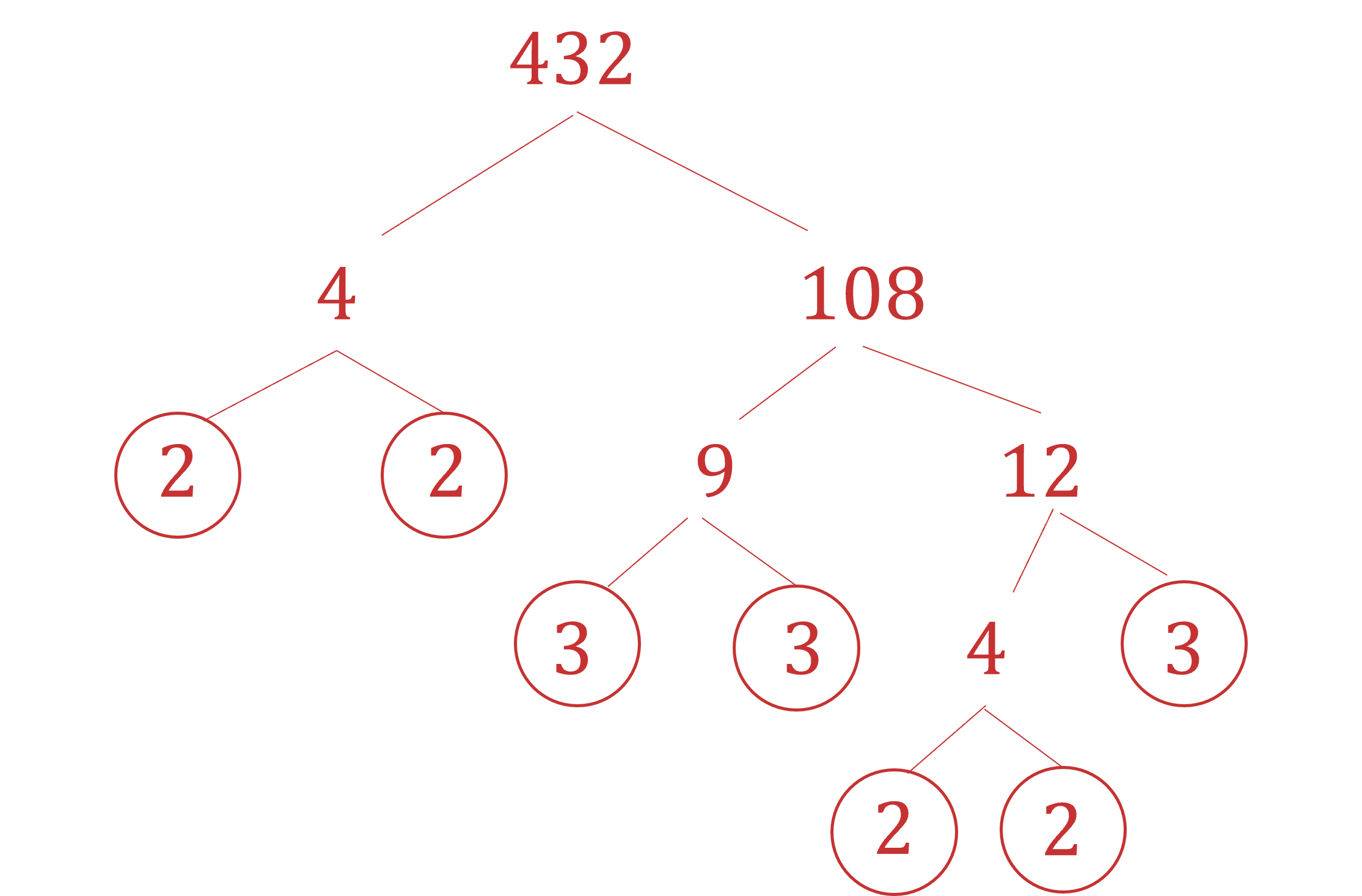
The answer will be the same regardless of the factors chosen in the first step
Write the prime numbers out as a product
Any repeated prime factors can be written as a power

Unlock more, it's free!
Did this page help you?