Exponential Growth & Decay (Cambridge (CIE) IGCSE International Maths) : Revision Note

Exponential Growth & Decay

The ideas of compound interest and depreciation can be applied to other (non-money) situations, such as increasing or decreasing populations.

What is exponential growth?

• When a quantity grows exponentially it is increasing from an original amount by a scale factor (or percentage) each year for years

  • Some questions use a different timescale, such as each day, or each minute

• Real-life examples of exponential growth include:

  • Population increases

  • Bacterial growth

  • The number of people infected by a virus

What is exponential decay?

• When a quantity exponentially decays it is decreasing from an original amount by a scale factor (or percentage) each year for years

  • Some questions use a different timescale, such as each day, or each minute

• Real-life examples of exponential decay include:

  • The temperature of hot water cooling down

  • The value of a car decreasing over time

  • Radioactive decay (the mass of a radioactive a substance over time)

How do I use models for exponential growth or decay?

• Scenarios which exponentially grow or decay can be modelled with an equation

• A useful format for this equation is

  • 

    • E.g. or

  • If then it is exponential growth

  • If then it is exponential decay

  • cannot be negative

• could model the number of flies, , in a population of flies, against the number of days,

  • The initial number of flies, when , is

  • After 2 days, the number would be

  • After 4 days, the number would be

  • From the values above, and the fact that , this is exponential growth

• could model the radius of a water droplet, , as it evaporates where is measured in minutes

  • The initial radius of the droplet, when , is

  • After 2 minutes, the radius would be

  • After 4 minutes, the radius would be

  • From the values above, and the fact that , this is exponential decay

How are exponential models related to exponential graphs?

• Plotting an exponential model, , on a set of axes gives an exponential graph with the following shape

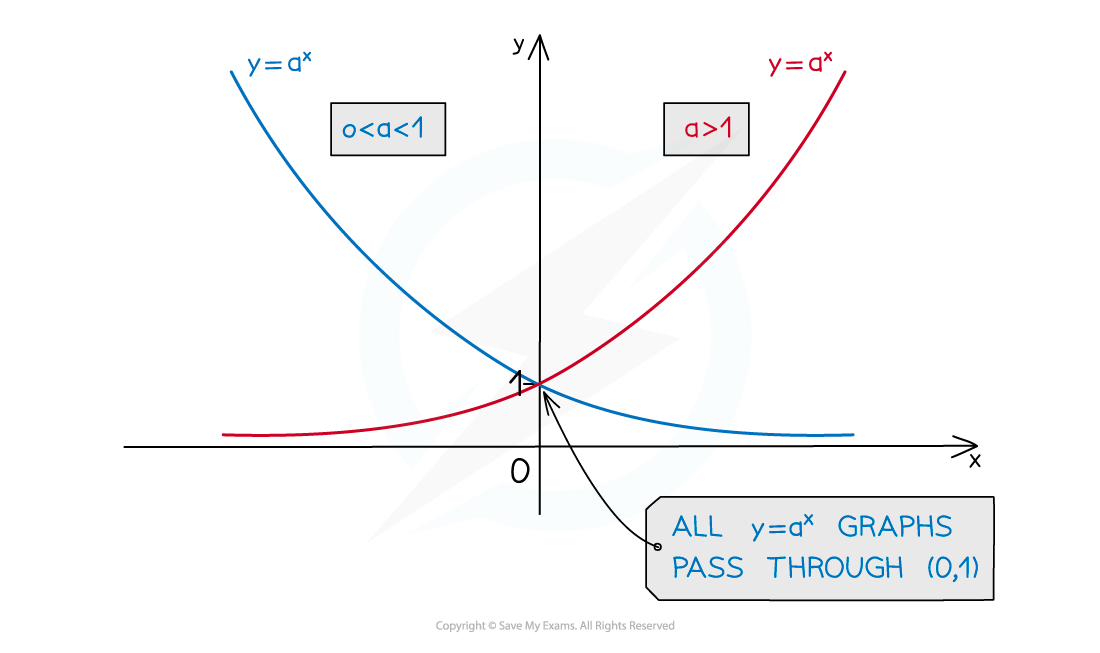
• The -intercept is always 1

  • This is because the -intercept is where

  • 

• There is an asymptote at (the curve gets closer and closer to the x-axis without crossing it)

  • This is because there are no solutions to

Are there any other exponential models I may encounter?

• You may see exponential models in the form

  • The coefficient, , scales (stretches) the graph vertically

  • The -intercept will be

    • This is because when ,

  • is the initial (starting) amount of the quantity being modelled