Bubble Sort (Cambridge (CIE) A Level Computer Science): Revision Note
Exam code: 9618
Bubble sort
What is a bubble sort?
In A Level Computer Science, a bubble sort sorts items into order, smallest to largest
It compares pairs of elements and swaps them if they are out of order
The first element is compared to the second, the second to the third, the third to the fourth and so on, until the second to last is compared to the last. Swaps occur if each comparison is out of order
This overall process is called a pass
Examiner Tips and Tricks
The highest value in the list eventually “bubbles” its way to the top like a fizzy drink, hence the name “Bubble sort”
Once the end of the list has been reached, the value at the top of the list is now in order and the sort resets back to the start of the list. The next largest value is then sorted to the top of the list
More passes are completed until all elements are in the correct order
A final pass checks all elements and if no swaps are made then the sort is complete
An example of using a bubble sort would be sorting an array of names into alphabetical order, or sorting an array of student marks from a test
Performing the bubble sort
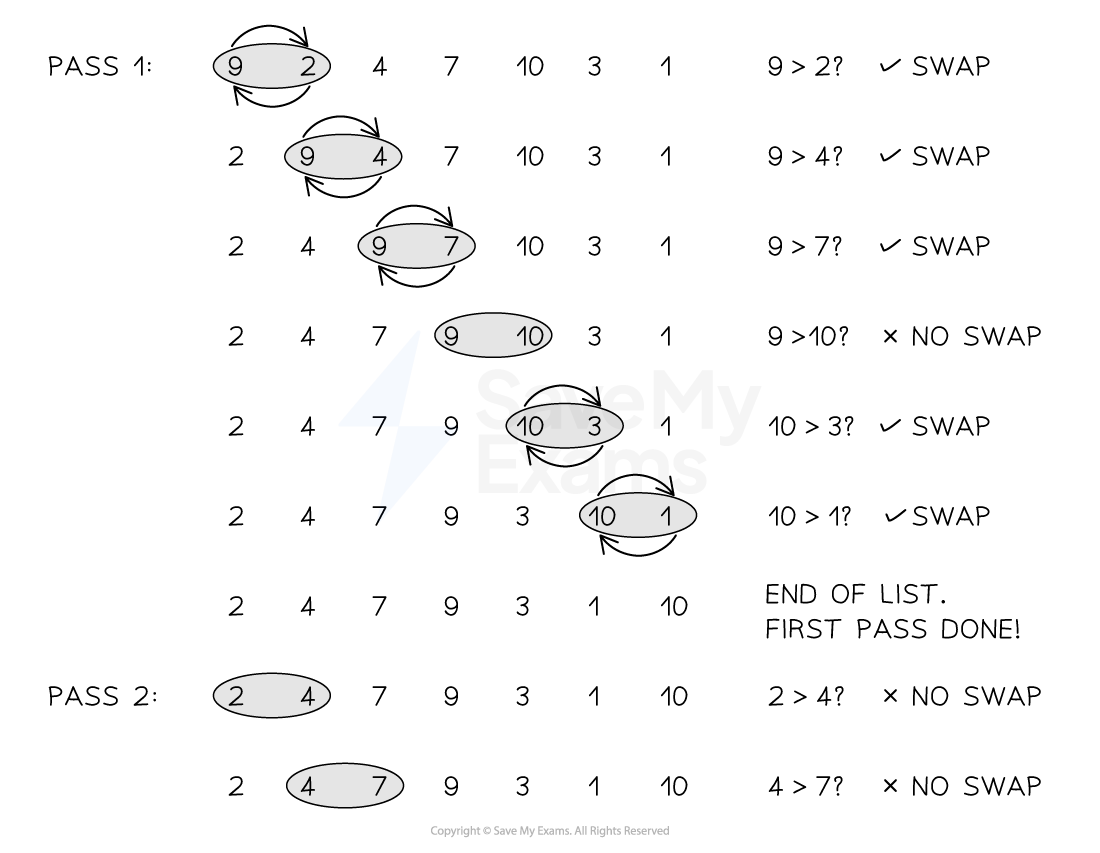
Figure 1: Performing the Bubble sort
Time complexity of the bubble sort
To determine the algorithm's execution time as measured by the number of instructions or steps carried out Big-O notation must be used
Four statements are present in the above algorithm O(1), followed by a while loop O(n) containing two statements and a further for loop O(n). This results in the expression: 2n2 + 4
As coefficients and lower order values are not used, this give the bubble sort O(n2) worst case time complexity
The best case scenario would be an already sorted list which means a time complexity of O(n) as each item must still be compared to check if they are in order
The average case scenario would be an almost sorted list leading to O(n2/2), which if coefficients are removed still gives O(n2)
Space complexity of the bubble sort
A bubble sort has a space complexity of O(1) because it operates in-place, requiring a fixed amount of memory
The fixed amount of memory is for variables such as loop counters and a temporary swap variable
Tracing a bubble sort
The trace table follows the algorithm through, updating values that change in the table
Each iteration of the list reduces the overall size of the list by 1 as after each pass the previously sorted final digit is in order and does not need to be rechecked. This means that 9 is in order and doesn't need to be rechecked, followed by 9 and 7, followed by 9, 7 and 6 and so on
When the if statement is checked a new row has been added to show the swap of list[j], list[j + 1] and Temp, followed by the subsequent change to Swap from FALSE to TRUE
After several iterations (that are not shown) the algorithm will eventually output a sorted list
Trace table of the bubble sort
LastElement | Index | Mylist[Index] | Mylist[Index + 1] | Temp | Swap | Output |
|---|---|---|---|---|---|---|
10 | 1 | 5 | 9 |
| FALSE |
|
| 2 | 9 | 4 |
|
|
|
|
| 4 | 9 | 4 | TRUE |
|
| 3 | 9 | 2 |
|
|
|
|
| 2 | 9 | 9 |
|
|
| 4 | 9 | 6 |
|
|
|
|
| 6 | 9 |
|
|
|
| 5 | 9 | 7 |
|
|
|
|
| 7 | 9 |
|
|
|
| 6 | 9 | 1 |
|
|
|
|
| 1 | 9 |
|
|
|
| 7 | 9 | 2 |
|
|
|
|
| 2 | 9 |
|
|
|
| 8 | 4 | 9 |
|
|
|
|
| 9 | 4 |
|
|
|
| 9 | 9 | 3 |
|
|
|
|
| 3 | 9 |
|
|
|
9 | 1 | 5 | 4 |
| FALSE |
|
|
| 4 | 5 | 5 | TRUE |
|
| 2 | 5 | 2 |
|
|
|
|
| 2 | 5 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
| FALSE | 1, 2, 2, 3, 4, 4, 5, 6, 7, 9 |
Implementing a bubble sort
Pseudocode
DECLARE list : ARRAY[0:9] OF INTEGER
DECLARE last, i, j, temp : INTEGER
DECLARE swap : BOOLEAN
list ← [5, 9, 4, 2, 6, 7, 1, 2, 4, 3]
last ← LENGTH(list)
i ← 0
swap ← TRUE
WHILE i < (last - 1) AND swap = TRUE
swap ← FALSE
FOR j ← 0 TO last - i - 2
IF list[j] > list[j + 1] THEN
temp ← list[j]
list[j] ← list[j + 1]
list[j + 1] ← temp
swap ← TRUE
ENDIF
NEXT j
i ← i + 1
ENDWHILE
OUTPUT listDeclare and initialise variables:
listis an array of 10 integers to be sortedlaststores the length of the listiis used to track the number of completed passesswapis a boolean flag to check if any swaps occurred in a pass
Set initial conditions:
i ← 0→ start from the first passswap ← TRUE→ assume a swap will happen to enter the loop
Main WHILE loop:
Continues while the list still needs sorting (
i < last - 1) and swaps are still happening (swap = TRUE)At the start of each pass,
swapis set toFALSE
FOR loop (inner loop):
Iterates through unsorted part of the list: from index
0tolast - i - 2Compares each pair of adjacent items
IF condition:
If the current item is greater than the next item, they are swapped
swap ← TRUEto indicate a change was made this pass
After inner loop:
Increment
ito shorten the range on the next pass
After sorting:
OUTPUT listdisplays the sorted list
Python
def bubble_sort(list):
n = len(list)
for i in range(n - 1):
swapped = False
for j in range(0, n - i - 1):
if list[j] > list[j + 1]:
list[j], list[j + 1] = list[j + 1], list[j]
swapped = True
if not swapped:
break # Early termination if no swaps occurred
return listJava
public class BubbleSort {
public static void bubbleSort(int[] list) {
int n = list.length;
for (int i = 0; i < n - 1; i++) {
boolean swapped = false;
for (int j = 0; j < n - i - 1; j++) {
if (list[j] > list[j + 1]) {
int temp = list[j];
list[j] = list[j + 1];
list[j + 1] = temp;
swapped = true;
}
}
if (!swapped) {
break; // Early termination if no swaps occurred
}
}
}Worked Example
A global 2D array Result of type INTEGER is used to store a list of exam candidate numbers together with their marks. The array contains 2000 elements, organised as 1000 rows and 2 columns.
Column 1 contains the candidate number and column 2 contains the mark for the corresponding candidate. All elements contain valid exam result data.
A procedure Sort() is needed to sort Result into ascending order of mark using an efficient bubble sort algorithm.
Write pseudocode for the procedure Sort().[8]
Answer
PROCEDURE Sort()
DECLARE Temp : INTEGER
DECLARE NoSwaps : BOOLEAN
DECLARE Boundary, Row, Col : INTEGER
Boundary ← 999
REPEAT
NoSwaps ← TRUE
FOR Row ← 1 TO Boundary
IF Result[Row, 2] > Result[Row + 1, 2] THEN
FOR Col ← 1 TO 2
Temp ← Result [Row, Col]
Result [Row, Col] ← Result [Row + 1, Col]
Result [Row + 1, Col] ← Temp
NEXT Col
NoSwaps ← FALSE
ENDIF
NEXT J
Boundary ← Boundary - 1
UNTIL NoSwaps = TRUE
ENDPROCEDUREOuter loop [1 mark]
Inner loop [1 mark]
Correct comparison in a loop [1 mark]
Correct swap of col1 array elements in a loop [1 mark]
Correct swap of col2 array elements in a loop (via loop or separate statements) [1 mark]
'NoSwap'mechanism: Conditional outer loop including flag reset [1 mark]'NoSwap'mechanism: Set flag in inner loop to indicate swap [1 mark]Reducing Boundary in the outer loop [1 mark]

Unlock more, it's free!
Did this page help you?