IGCSEMathsCambridge (CIE)ExtendedRevision NotesGeometryAngles in Polygons & Parallel LinesAngles in Polygons

Angles in Polygons (Cambridge (CIE) IGCSE Maths) : Revision Note

Jamie Wood

Written by: Jamie Wood

Reviewed by: Dan Finlay

Updated on

Cambridge (CIE) Maths: ExtendedEdexcel Maths A: FoundationEdexcel Maths A (Modular): Higher Unit 2Edexcel Maths A: HigherCambridge (CIE) International Maths: ExtendedCambridge (CIE) International Maths: CoreCambridge (CIE) Maths: Core

Did this video help you?

Angles in Polygons

What is a polygon?

  • A polygon is a 2D shape with n straight sides

    • A triangle is a polygon with 3 sides

    • A quadrilateral polygon with 4 sides

    • A pentagon is a polygon with 5 sides

  • In a regular polygon all the sides are the same length and all the angles are the same size

    • A regular polygon with 3 sides is an equilateral triangle

    • A regular polygon with 4 sides is a square

What are the interior angles and the exterior angles of a polygon?

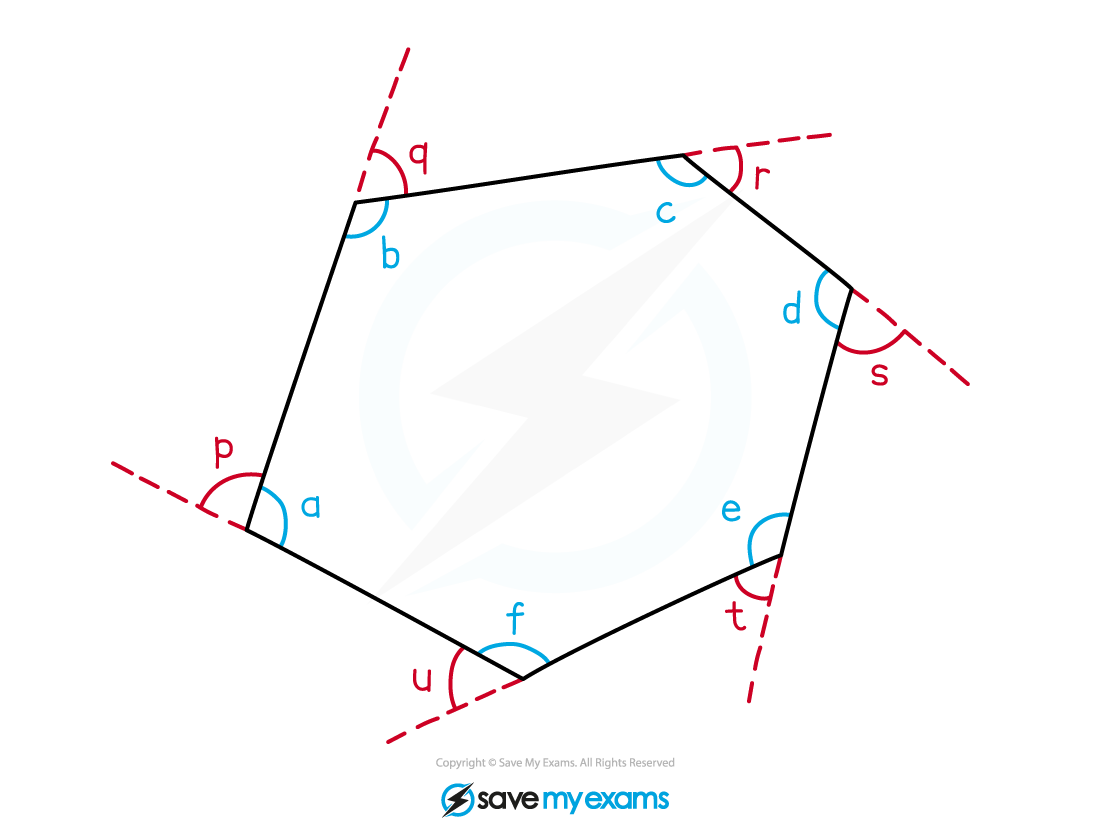
  • Interior angles are the angles inside a polygon at the corners

  • The exterior angle at a corner is the angle needed to make a straight line with the interior angles

    • It is not the angle that forms a full turn at the corner

  • The interior angle and exterior angle add up to 180° at each corner

interior and exterior angles summing to 180 degrees
Interior and exterior angles in a hexagon

What is the sum of the interior angles in a polygon?

  • To find the sum of the interior angles in a polygon of n sides, use the rule

    • Sum of interior angles = 180 degree space cross times space left parenthesis n space – space 2 right parenthesis

      • This formula comes from the fact that n-sided polygons can be split into n minus 2 triangles

  • Remember the sums for these polygons

    • The interior angles of a triangle add up to 180°

    • The interior angles of a quadrilateral add up to 360°

    • The interior angles of a pentagon add up to 540°

What is the sum of the exterior angles in a polygon?

  • The exterior angles in any polygon always sum to 360°

How do I find the size of an interior or exterior angle in a regular polygon?

  • To find the size of an interior angle in a regular polygon:

    • Find the sum of the interior angles

      • For a pentagon: 180 degree cross times open parentheses 5 minus 2 close parentheses space equals space 540 degree

    • Divide by the number of sides (n)

      • For a pentagon: 540 degree divided by 5 equals 108 degree

  • To find the size of an exterior angle in a regular polygon:

    • Divide 360° by the number of sides (n)

      • For a pentagon: 360 degree divided by 5 equals 72 degree

  • The interior angle and exterior angle add to 180°

    • Subtract the exterior angle from 180° to find the interior angle

    • Subtract the interior angle from 180° to find the exterior angle

Regular Polygon

Number of Sides

Sum of Interior Angles

Size of Interior Angle

Size of Exterior Angle

Equilateral Triangle

3

180°

60°

120°

Square

4

360°

90°

90°

Regular Pentagon

5

540°

108°

72°

Regular Hexagon

6

720°

120°

60°

Regular Octagon

8

1080°

135°

45°

Regular Decagon

10

1440°

144°

36°

How do I find a missing angle in a polygon?

  • STEP 1
    Calculate the sum of the interior angles for the polygon

    • Use the formula 180 degree cross times open parentheses n minus 2 close parentheses

  • STEP 2
    Subtract the other interior angles in the polygon

Examiner Tips and Tricks

  • Make sure you identify whether you are dealing with a regular or irregular polygon before you start a question

  • Finding the sum of the interior angles using 180 cross times open parentheses n minus 2 close parentheses can often be a good starting point for finding missing angles

Worked Example

The exterior angle of a regular polygon is 45°.

Write down the name of the polygon.

The formula for the exterior angle of a regular polygon is Exterior space Angle equals fraction numerator 360 degree over denominator n end fraction 

Substitute the 45 for the exterior angle

45 degree equals fraction numerator 360 degree over denominator n end fraction

Solve by rearranging

table row n equals cell 360 over 45 end cell row n equals 8 end table

Write down the name of a shape with 8 sides

Regular Octagon

👀 You've read 1 of your 5 free revision notes this week
An illustration of students holding their exam resultsUnlock more revision notes. It's free!

By signing up you agree to our Terms and Privacy Policy.

Already have an account? Log in

Test yourselfFlashcards

Did this page help you?

Previous:Basic Angle PropertiesNext:Angles in Parallel Lines
Author
Reviewer
Jamie Wood

Author: Jamie Wood

Expertise: Maths Content Creator

Jamie graduated in 2014 from the University of Bristol with a degree in Electronic and Communications Engineering. He has worked as a teacher for 8 years, in secondary schools and in further education; teaching GCSE and A Level. He is passionate about helping students fulfil their potential through easy-to-use resources and high-quality questions and solutions.

Dan Finlay

Reviewer: Dan Finlay

Expertise: Maths Lead

Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

Download notes on Angles in Polygons